R2.C(1/2)
R2.C(1/2)-
R2.C(1/2)+
Robert P. Munafo, 2003 May 19.
| R2-Name: | R2.C(1/2) |
| Abbrev: | RC(2) |
| Colloq.: | Seahorse Valley |
| Coords: | center = -0.75+0.0i, size = 0.4 |
R2.C(1/2) is the R2-Name for the two large cusps between R2a and R2.1/2a. The upper half of this cusp, R2.C(1/2)-, is more popular probably because it was featured in the 1985 Scientific American article.
Like all cusps, this cusp features two sets of radicals converging from either side and asymptotically becoming more and more similar in appearance despite having radically different topology. Approaching R2.C(1/2)- from the upper-right, we have the radicals R2F(N/2N+1(*B)), and approaching from the upper-left we have R2F(1/2(1/N(*B))). As you ge closer to the bond point at the bottom of the "valley" you can see that these radicals alternate, with R2F(N/2N+1(*B)) situated across from and about halfway between R2F(1/2(1/N(B))) and R2F(1/2(1/N+1(B)))
R2.C(1/2) is known as Seahorse Valley because of the seahorse-like spiral 'tail' appearance of each R2.N/2N+1 radical's longest branch filament R2F(N/2N+1B2) (see figure 3 for an example).
There is another, longer zoom sequence in the Seahorse Valley entry.
 -0.750 0 +0.080 0i @ 0.160 0, Nmax: 20000 | ~.__@Y` '("(^` ^^^^^*FdF '"b@ca_._Y\- vdL^_/Y^ 'bm*\v@@`.__, _,/@@@F^"` '`__@*`]b\"` '****YL_c '"-@a,_d\- a@`.@C '*~^\@@\__, __@@F"^` 'vdF,"(^` '*YC"br "@)d$@`__ .:@vr@- '.a@^*@* '@@*e_ "("m@c_, v@_@` '-@^*@` "@Fb_ '"@@__ ._dm*c ^@d$^ "@"m ':F") -m@%^ '^7be ._b"- '*de, /@* "d_ T%` ')b, .$F` '@b -d( ]T; :bF R2a Yb -@[ R2.1/2a '$c '@ 'b ]C Y,]F ]c][ b][ ]] '] ] ] Coordinates: -0.7578 +0.0988i @ 0.161 |
.jpg) -0.745 48 +0.116 69i @ 0.012 76, Nmax: 17290 | a;@@(-.d@Fvm@^Y)@^@%YdY@%YdC$@b-@@@@/-d@@@$@@@C@@@Cmb@@@@@F^^@F` ''^` *Y@@L_$@^*C"Y/Y@%@r*"^" '^ "^` ^"*@@@@@@@b/*Y@@L, _@@@Y` '*"'^"@"~Y"^*''` /dd@@@@"^_ '^-@mm($@L- .._ea_m_, '^***^.aF*` :m@@@@Y** __@@*^^^^Ybc :@@m,a__^7Y@@@_/ ._aCC*` @7`a@* 'Y@@bF@@Fe_/@$@F- .F*$F` '"*"^` __]@@@@@@Y)@@F@b@" -db@@C@mc | '@@@d@@@@@@@**" '` _:F"*L@F A 'T@@@@@@@@@@@me._._ __ :Cb(dFT@_mm_ '^^^"**@@@F@@@\@" .m@^e@@@Cbead@@C^ __m_, m_am@^@F '"@_m@/@^- .b@@@@@7m*Y@^@FTmr. :d@@@LadmCY@bb .e@@@@F*" ^^%%^`*vad*^@@@@@m_'@@@@@@@YFb""$ame,_d@*@@@bm v@;^` .,@@bv@"^ a(['@@@@@$@@@@rd@@@@@F'`d@@F" _e@@bm,,$Y@@bd@m, .@@@F"d$@^*@b@@*Y@@bm*"@@/ '^*^^@bC,`db@Y@b_ .____@cd@m$@@, ^^' ^^^Y@bF@) -@"mm"$@m-F@@%F**b]@@@@@%T@@C^ '"@d` .___e. v"m%@@%@$)m@@@F _^d@F@@d@@@@` '@` .a*Y@"^^"c.@@b@@7@v@\m@b^T:@m@v@d@` '` R2.13/27a ' __d-e@dm@^ ""\d@@@@@@@d@d@"Tmm$@@@@@ba_,.__ '"LY@@@d"@be,-@@@@@@@@@@@$d@F@@(@@@^$C@@d@@@_ . `^^^-- ^F^@$$Y@@@@@@@@dmbmb_a@,_$@@@@*-@@@b,, ..m[ -Y"e_m@Y^$mY)$Y@@@@F@@@dC@*@@@@).'^$Le@F@@@`ae__._,_a@%@ d@@F^ :@C'@C$YYC@*@@@@@@Y@e$b@@/bm$@@@@m@@@@@@@d@@C^bF- '"""'mmdF'*b(@"C*@*(@@*""^^^ "^` '^*@@@@@@b"*@@(c./@@*` ]*"-Y@-*c**^`' . , :d@@@@"L_, (@@@@@r R2a _amm**dm, ^^^./L^`, (@@@@^^` -m@F`.mm\@@, _@@@v@d@^"@(FF :v@@@ '"mmF* .@@d@C@Y@@@@@c _m/b/@L, 'vdmd@@@@@@**^ '"` Coordinates: -0.74407 +0.1174i @ 0.01155 |
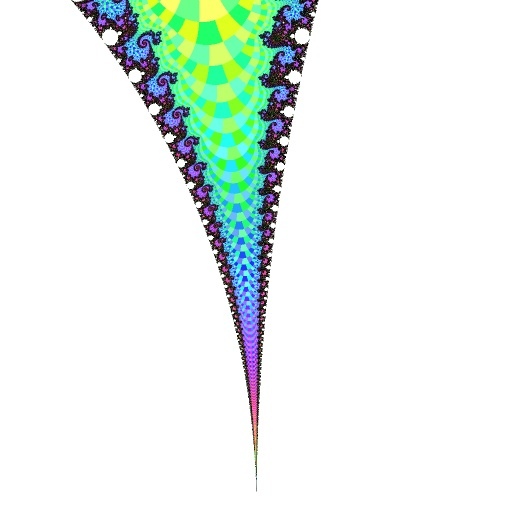
 -0.744 567 +0.121 201i @ 0.002 000, Nmax: 17290 | me_, ._ mea_ _ :d@@^".,., :_/@m, v@@LC_ac(mm-,@@@@@@Cd@mm,d@@@/" meae, ,.e___/@@@@@+=====+@@@@@Cb@).'\@@@@@@@\mc, ._.m, -m$@_LmdC$$"'"]@F@F|/"^)/|*~@\CC`%$/b@C@@C@@%@**\.a@@@*@r "@@@@@@Fm@@e-@F""\|m_d"Y|"_m@d@m'@^c.'Crd"^*F__%d@@@@C^` _/mmb*a/YF@@F"F`'m$d7`.d|@@@@e|"YFFY@@b'Ymm@bd@,]@[*FC@$@@@@be_, m@Y%@C_ ./d@**T"@mmm_^^"*+=====+ 'F*^ '^"@@@[]/"_-@C"bCF%Y@@e @@@\d$F"e%$vc.dC@@@@@b ' '**^ '$@C@ed*``*F^ dF__mmeam @F@Y@` '`**--Y*Y^^'** :@@@@.m@"(@mmd@@@@*@@ ($b/d/bmmmme, '***`@^^ :@]Y@@@@@""^ FL'`$bY@@@@@@- -Y@dm'@^@%Y$@@b d"`_m@@*"'"*` ._ ._ ad@@@@*^*\CL/vb)- d****^^ :__aT@F$@\md__ ^*F*(/vmm/"^'^@" ___, _aa*@@$/*"""*Yd@, .:@/^^:@@adL%__ @@@@L, 'Y@@C$% ___,'T@@` ._a@b@)aYb(@@@@@@ @YY@@, _:@bYdC YL^`_@@" '@@@@@mY_/$@@@@F% `'^^^` -Y@@@*YF` "***"^ '^%Ye, TF(Y$@@`' aC/"(mm .___d@`^*Y-"**e$mL _d@bCF*b.__ ]@@@CF\m_(@;.c$F^` "**(^CF*/@@_ ._, .me_a_m"^^"(%dC@@@bm_, "@@C@$F^%bY@bmmedY@@@F ]d`.$C)@@@@@@@@c ._Y@@F""@%_F@^:mF`^)-b)m/"^*@$m@@"@%@dm_ , F**"'bdC@@@@@F"Ym/%@b@@@:ed@YF^ '^"` ` '^**@@@@v_m$"@@@@@@b '@@@@` '^*'^^$C@@F` ^` '"^*` Coordinates: -0.744423 +0.121295i @ +0.001444 |
Compare figures 1, 2 and 3 to the ones in the entry for R2.1/2.C(1/2) .
 -0.744 538 92 +0.121 724 18i @ 0.000 100 00, Nmax: 17290 | d@@b_ `` ,.amd@@@@bm,, .aC,:@@@FL_F@m_/dCC^"*) @@@F . ._d@@@@@@@@@b@*` :mm@@C*me d@@*`'$@F.a,a@ @eb@C adbmd^$dF$@@@@@^"" "*@*^*'mam-mmmc__m"*%%^^ '`'^*b,^Y@@@C\_YC@@@C@\_ ., ._mC'` .a@@@bmm^"@@@@$$^ . :F":@m___, 'YYaa**@d*Y_._ :_mYbre_am%@(me_,"***"`' d@@@"_a" ^"""Y@,"`_:mC)@,vdvmb@@* -aC@@@mm@@@T)@"*^^%ve_mm, '^av@@* _m_ea___'"*\@@@@@@@cYL_@*@Y__ -Y@F@@@@@@@Y$FY`,'^^*@,"" :mm@;'^_d LYY$@@@@m, ^ 'F* ^T@*@@*b_, '@C@@@@@@@@@m7F@@@me/^*ddb-C7\F@r*@ *Y@@@@@@@@, '*'@@m_ '*$Fb@@d$*mb_$@*@@@` T@Y$b@@@@C@ "Y@@@*Y$bC ^)@@m, ''*^*'Y"^"* ^^^ '^*@@@@@@ F@%F` ._amm_, 'Y@be .dCd@@@@@ Y@@*- .@@".rT) '@"@db,._ '""@@@@*^ @F- '*@@,,^^ m@@"*FTd@m.de_m__, ` F` .__, -*@bbae,m_e-*+==+%"@CF$@*@Y@be_ - ._m@@@ba, '**b@*(@@dL| |*"*^^ _ ^"@@_ 'm@ :@@@@@@* "`"Y@@^^+==+@@- :m"$ .@@_ ._ :dL ]@@@@@@bec,... ^`'*@@@F$\, *bmm@*" (dCe@@@ -*%@7)b@^^b]@@_,._, '*"L@%@@_, ' T@@@@@@ v@@.m/^_,_@(@""]@L,._ ]@Y\F@C_, ., ,. '"**YY ..m^$`@@@F""d@r@(%:@@m._ '$@@dY@m,mc, ._ m@bam@@**"ve__ bmdY@,__'C@\@m*(m_@@^$b/@@\__ ' ^@@@(b@FY\Y@mdme"@@@)@- '*-YL- @@@CTbY@FL__\*b/*br@%^bad*m@"__, ^^'*@@F"@L$(ed)@c'Yd"d_ammm/" v '*]7`')*"@)m%$C$@/@/@v@"d*m@Fc_, '*"'YY@@@@"^/md*)m$mF$F^` ;,am@@m@Yb*@vC@@(@$b@dCdCdF-/*aY@; m@@""mdFd@@@@@@@.mc @@$v@^$maFdYC@b@@@@@@dbFd@$@Ymdc/bm- '^ ^'^"F@@@@@ "mm *(^`@@d@$r@@@@@@@@@@@@@Y$/C@FY_$)*@_ @md*@$` ^ dF\mdbe$C@@d@@@@@@@@@@@$bYC$md`Ymmb@b "@``' ";:YCmd@-@(bL@@@@@@@@@b@C@^C_@@m@"YF F@-Y@%d@LY/@Y@@@@@@F@b@d^$^^F^:Tm_$be, '^ '^^'^`^^^^^^^^`^'^^^^`^'^^`^`^^^^^ Coordinates: -0.7445385 +0.1217199i @ 0.0001804 |
 -0.744 539 761 +0.121 724 001i @ 0.000 006 250, Nmax: 17290 | '*@@@**@F` -@FF@@*` -FFm*@$F :a@%/@aL*__,, ._a@^@/C,, :@FT@@@ -_mv.dbC@C'^a@@@*` "YF**@@@" ^@Ydb (d@@@@@$^)C^@F@@_ ._be__mm"@(d^$F '* ., :___ __,_%*@@@d"@@m^"*"@@m ]@@@@@@@@_m@@@m@@m, d@)..,_-d@C@_arY@@^-* *C$Y@, .._ ^@L *@@@@@Ym7b$@@@@C^ @@@@@F^c@@@@@b@"Cbm -m@@@@ :@^@) '@L ^^^^`'`'*Cm^@$m, _ Y$@"$cmd@Y@@$Ld@$@@m_,^***` (@_ ._/@@m_.___aaa, ]@@Y/""bamm@m , @@@cYY(^'@Fd:@*` ^'^*Yme_a__d@@**e"*^%Y^$@@@^ v*.aF^__ ^%d@@@bma__a@r_ (@@`'b__md*^mr .m\m '*@@@Fe/*]/d@d@]d(%r/F.__edF a@@m($@@Y@@@@"/@@@@ "Y@d@@$Cb $@__, v@@`:$'@T)@@@@@@@dadL^*YdF '**F\*v@FLY;~@F^^@m ._$@@@@@@ -Y@db-vd__/@T$@@@@L'**YY@@CC@/%@me__,_ '^T%$@mm%^"^" '@@@@@@F^ -(@@L:$,Y"@$Y@@@^ "@@d@_%^@@F*"*m d@@T@F@@` '^^""` __ma@L$C_FFC@@b@@@- 'Y@@)%d)*`, '""../@F@^ .,_amb@@C@C-md*]d@@@^^^^ "@@dC,Y@b_eammF"^ :_,__mm@*^._, '**_$bb@@@@^, _a, .%@@\^T_$@@**^ ____. ]@@@@/L; (C%.am^-@@@d@@@@@bm@@@bm.__,-m@@FF@^$FT*^ .d@@@@@m- d-\^*@@%F_, '^^"YY%/CF)@(7@@@Y$@C@@@@@bm@@@T@^)'@@C, -@@@@@@C^ b/@YC.$$]@"emmm_, -@Fmmc$^;@*Y@r~e%FF*F@@@F@F^%^"*"@L $F@YFF@bm _,_ @@m_@$d@b@md)*@@[.dF` ^`@m%amr@-e*^^*@^$"%)%_@Y` .v:@ :@FL$F*""b-d@@ "` ^^*@@@@F%; adF m"_.@@@@)_@ber@@m^med@m***Y@e_^^ ._m""bm.d*de"@* '\FY" \L_:m@@` '"*"^^ ' "Y@dC'` 'T@C' .__,'^*dmb-CFY*m$b@F*"Cad% -F)@%b(m- _ .a__._ -Y@c :r-_@` .d@@@b $@Y^@@@@@@@-ed@Y@@ .dY@d@@F^e*@@b@@@@m, 'Y@, ^^^` :b@Fb, .,ad$C$d*YF@@[ ^''@ ]b@@@@b@\*bd$@@@@@@[ '@@me.,,._mC%@$be7""*^" '**` '$r^@*,,^@C*"@@@@` .@@dT@"m%^Y$Y@@@@be b, .d@C@^*%%^` ^ ."@@@@F~v@b@@@FF@@, ^bm "@@@@F$@Y@` -\@@F^amaY@@$" ^^ @C@_ .:@e@"*^ .d"*a@,e*^ `^^` '^^^^^^` '^^'^^^^^ Coordinates: -0.74453945 +0.121724i @ 0.00001128 |
This cusp has a number of special properties:
It is the Largest Cusp in the Mandelbrot Set and therefore the easiest to explore. It is larger than R2.C(0) mainly because of the inverse-square size pattern of the mu-atoms; the mu-atoms in R2.C(0) follow an inverse-cube pattern (see the formulas in the secondary continental mu-atoms article for details).
Exact Coordinates: The mu-atoms R2a and R2.1/2a touch at precisely -3/4 on the real axis.
Relation to Pi: One really surprising fact about this cusp (and also seen in R2.C(0)) is the relationship of the dwell band spacing to pi (π). All points with a real coordinate of -3/4 are not member points, except for the point on the real axis, -3/4+0i. If you look at a point C=-3/4+i/x for some positive x and count the number of iterations it takes to escape, the result is almost exactly x times π, as demonstrated by these examples:
|
This relationship actually occurs in all the cusps, and it is caused by the fact that, for sufficiently small values of epsilon,
(1 + epsiloni)π/epsilon = -1
which is also related to Euler's derivation of the famous relation ei π=-1.
From the Mandelbrot Set Glossary and Encyclopedia, by Robert Munafo, (c) 1987-2024.
Mu-ency main page — index — recent changes — DEMZ
This page was written in the "embarrassingly readable" markup language RHTF, and was last updated on 2011 Jan 19.
 s.27
s.27