Atom Domain
Robert P. Munafo, 2023 Jul 7.
An "atom domain", or dominant period region, is a region (a connected set of points) sharing a property that is easily computed and makes for a good representation function. This method was first described by Peitgen and Richter in The Beauty of Fractals (1986).
An atom-domain region always includes the nucleus of a mu-atom. All the points in the region share a property relating to the values of iterates, that can be qualitatively characterised as an approximate periodicity that aligns with the exact periodicity of that nucleus. It can be said that the mu-atom "dominates" the orbital dynamics of points around it, often including exterior points.
Rendering Mandelbrot images with atom-domains in different colors makes it easy to find certain island Mu-molecules and embedded Julia sets.
Given a single specific point, one can easily find a number that is equal to the period of a nearby mu-atom. This might be called a "nearby dominant period", "period of the dominant mu-atom", or a "tuning" period. It does not indicate that the given specific point is inside that mu-atom or any other, even if the point is known to be in the interior.
Contents
Size Relationships for Islands
Origin
The first atom-domain image appears in The Beauty of Fractals, figure 34 (on page 61), with this description on the following page:
Fig. 34 (see p.61). Domains of index (c)-constant (see (4.24)) for c∈M. Indices organise according to Fibonacci sequences. [...]
Figures 33 and 34 are included from some ongoing research on M. Given c∈M we define
(4.24) α(c) = inf { |pck(0)| : k = 1, 2, ...}
and
index (c) = k provided α(c) = |pck(0)| .
[...] Fig. 34 shows the distribution of index (c) on M. Remarkably each satellite is distinguished by a component of some fixed index and index (c) introduces a Fibonacci partitition in M.
"pck(0)" had previously been defined as the standard iteration algorithm for the Mandelbrot set. The "Fibonacci partition" does not refer to the type of partitioning related to OEIS[A0119], but rather to the Fibonacci sequence which arises out of Farey addition looking at periods of secondary continental mu-atoms; see these articles by Devaney: 1997, 1999.
Definition
Starting with the standard iteration calculation:
Z0 = 0
ZN+1 = ZN2 + C
and defining RN=|ZN| (where "R" stands for "radius", i.e. the distance from the origin to ZN); the period of the dominant mu-atom or "dominant period" is:
Atom-Domain = N(minimum(Ri))
This is the value of N when RN=|ZN| reaches a minimum (not counting the initial value R0=|Z0| which is always zero). In other words, the Nth iterate is closer to the origin than any other iterate(s).
This concept of "some number n for which the value of f(n) is a minimum" is what is meant by the "inf" in the Beauty of Fractals quote above.
 | 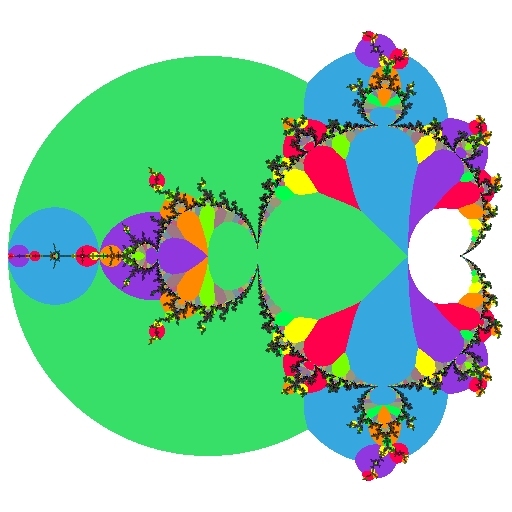
|
Above we see (on the left) an ordinary view of the Mandelbrot set and (on the right) the same view showing atom domains. All of the points in the green area have a dominant period of 2. This means that when iterating these points, the value of Z2 has a smaller magnitude than all of the other iterates (except for the initial Z0=0, which does not count).
Similarly, all the points in the three light blue regions have a dominant period of 3, so for them, the Z3 iterate is smaller than all other iterates.
In practice, we can only compute ZN2+C a finite number of times. A calculation of the atom domain ends up being just the same as the normal Mandelbrot calculation, except to take note of which iteration produces the smallest value of |Z|. In pesudocode, it comes out something like this:
function atom_domain param(c) : complex param(max_iterations) : integer param(escape_radius) : real should be 2.0 or larger result: integer begin function declare z : complex declare iterations : integer declare still_iterating : boolean declare minimum_n : integer declare minimum_magnitude : real let still_iterating = true let iterations = 1 let z = c let minimum_magnitude = magnitude(z) let minimum_n = 1 while (still_iterating) do let z = z2 + c let iterations = iterations + 1 if (magnitude(z) < minimum_magnitude) then let minimum_magnitude = magnitude(z) let minimum_n = iterations end if if (magnitude(z) > escape_radius) then let still_iterating = false else if (iterations >= max_iterations) then let still_iterating = false end if end while let result = minimum_n end functionThis function yields an excellent way of locating mu-atoms of a given period. The image produced contains regions of solid color that surround the mu-atoms, because the minimum RN value occurs when the number of iterations is equal to the period of the mu-atom.
In the images below and in the second-order embedded Julia set article, each color corresponds to an atom domain value.
If desired, a "maximum atom_domain" parameter can be used in the algorithm, to detect certain low numbers without interference from the many higher numbers that always occur near mu-atoms. Here are four images of the mu-molecule R2F(14/15B1)S in Elephant valley an island whose period is 17:
s-apd34.jpg)
atom domains 17 and 34 | s-apd51.jpg)
atom domains 17, 34 and 51 |
s-apd68.jpg)
atom domains 17 through 68 | s-apd85.jpg)
atom domains 17 through 85 |
Island mu-molecules and their surrounding embedded Julia sets can be located by this method. To make this easier, some other quality such as brightness or saturation could be altered based on the relative magnitude of the minimum radius RN.
Properties
For cardioid mu-atoms, the size of the atom-domain is typically much larger than the cardioid (qualitatively, for non-tuned islands, the "diameter" of the cardioid's atom-domain "blob" is approximately the square root of the "diameter" of the cardioid. Since the "diameter" of the cardioid is a very small number like 0.000001, its square root is less small, like 0.001, and therefore much bigger by comparison).
The atom-domain of any .1/2a descendant of a cardioid (i.e. the largest circular mu-atom on any island) is a roughly circular region with diameter 4 times as great as the mu-atom itself. In the case of highly distorted mu-molecules, the .1/2a's atom-domain is an ellipse whose major axis is somewhat larger, and minor axis somewhat smaller, than 4 times the .1/2a mu-atom's diameter.
Regardless of any distortion, the boundary of the .1/2a's atom-domain, and the boundaries of the atom-domains of all mu-molecules in the island's R2t series pass through the tip of the island (the most extreme point of the .F(1/2B1) filament). Here is an example:
s.jpg) | s-apd.jpg)
|
Here we see the highly-distorted island from the R2.C(0) article. Note the mustard-colored ellipse belonging to the .1/2a mu-atom, the red ellipse belonging to the .F(1/2B1)Sa island's cardioid, the blue ellipse belonging to the .F(1/2B1)FS[2]Sa island's cardioid, and so on, the boundaries of which all pass through the tip.
Other descendants (non-cardioid "circular" mu-atoms) whose name ends in .1/2a (such as R2.1/3/1.2a) also have an elliptical atom-domain. The ellipse passes through the nucleus of that mu-atom's parent (in this example, passing through the nucleus of R2.1/3a) and also passing through the tip of the parent's mu-unit (in this example, the branch point R2F(1/3B*)). Again, the ellipse has a major axis somewhat more than 4 times the diameter of the mu-atom and minor axis somewhat smaller.
All other descendants have a atom-domain with a teardrop shape, of a width about 3 to 4 times the mu-atom's diameter and a length about 6 or 7 times the mu-atom's diameter. For descendants ending in .1/3a and .1/4a the teardrop's tip touches the parent's nucleus; in the .1/4a case it tapers down to a zero angle (like a cusp). For higher-order descendants the tips do not reach the parent's nucleus. The rounded end of the teardrop extends some distance past the mu-atom (in calculated images this is usually obscured by the domains of other mu-atoms with higher periods).
Size Relationships for Islands
For islands that do not have any tuning apart from their own, there is no single direct relationship between the size of the island and of its atom-domain. However, there are classes of islands that have a direct size relationship to their atom domains.
Here are the first few islands in the R2t series. As discussed in that article, their sizes diminish by 16 each time and their locations get 4 times closer to the tip. Since the atom-domains are all mutually tangent at the tip, it follows that the atom-domain is 4 times smaller. Thus we can see that for these islands, the size of the atom domain is approximately the square root of the size of the island.
|
For the islands in this table, the relationship is approximately:
sizeisland ≅ 0.1 (sizeatom-domain)2
or equivalently:
sizeatom-domain ≅ √(10 sizeisland)
For other non-tuned islands the relationship is a bit different.
Islands that are part of a mu-unit smaller than the entire Mandelbrot set R2 are tuned, and always have a composite (non-prime) period. Here is a series approaching the Feigenbaum point from the west; As above we start with R2F(1/2B1)S but each time the period doubles.
|
In this case the relationship is simple: the atom-domain is about 20 times the size of the mu-molecule's cardioid. Each step involves an additional tuning factor of .1/2, and the scaling factor at each step is the Feigenbaum constant ≅ 4.67.
Examples
 | 
|
Here again is the full view of R2. The colors are: white for 1, green for 2, blue for 3, purple for 4, red for 5, and so on. Note in particular that small color "bubbles" around the various islands such as blue period-3 around R2F(1/2B1)S and smaller purple around period-4 R2F(1/3B1)S.
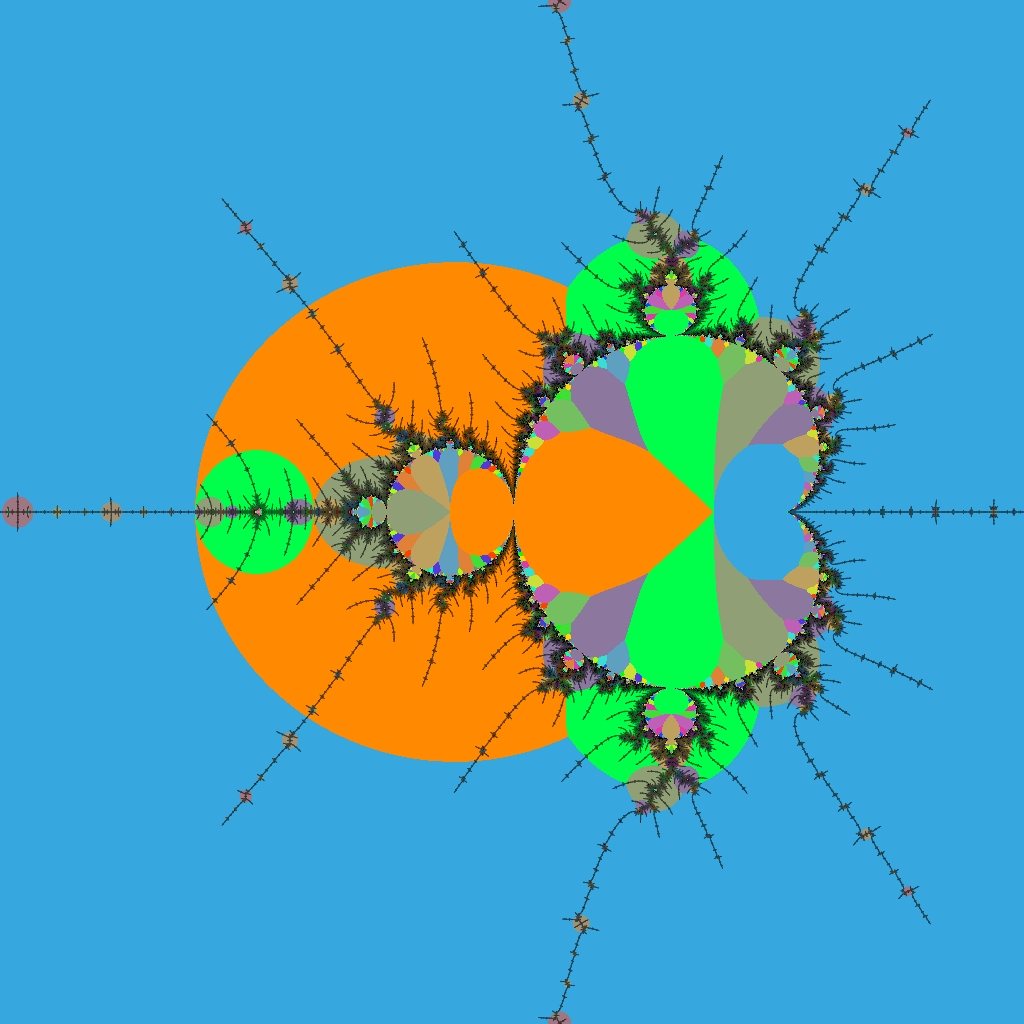
 | 
|
This view shows the immediate vicinity of R2F(1/2B1)S. Periods that are multiples of 3 (the island's period) are most prominent, and the locations of embedded Julia sets around it are made clear.
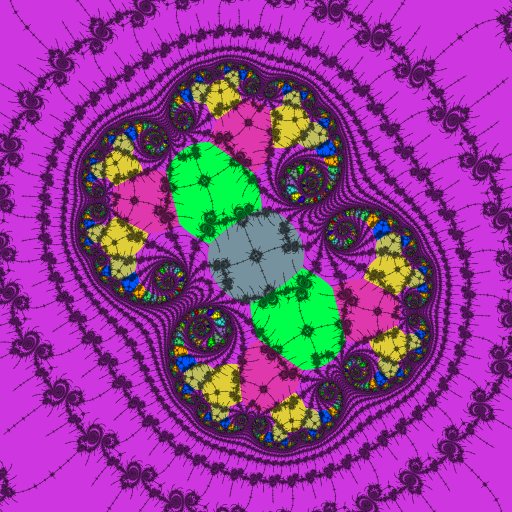
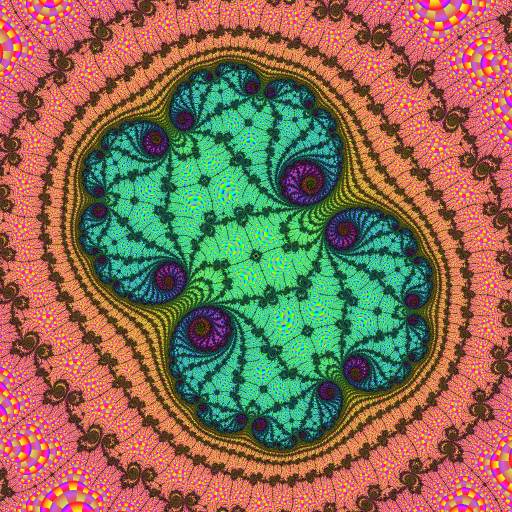 | 
|
Here the atom-domains clearly show the locations and periods of the nucleus and paramecia of a 2-fold embedded Julia set.
Several more images with atom-domain coloring are included in the second-order embedded Julia set article.
revisions: 19961024 oldest on record; 20120421 add images; 20120422 expand description, add tables of measurements; 20120423 add Feigenbaum sequence; 20120424 extend algorithm description; 20120529 add distorted island example and table of contents 20121202 no simple size relationship for cardioids 20141105 add Peitgen & Richter quote; 20230319 add mu-atom periods to the tables of examples; 20230707 reference Devaney on the "Fibonacci" topic
From the Mandelbrot Set Glossary and Encyclopedia, by Robert Munafo, (c) 1987-2024.
Mu-ency main page — index — recent changes — DEMZ
This page was written in the "embarrassingly readable" markup language RHTF, and was last updated on 2023 Jul 08.
 s.27
s.27