Notable Properties of Specific Numbers
Introduction
These are some numbers with notable properties. (Most of the less notable properties are listed here.) Other people have compiled similar lists, but this is my list — it includes the numbers that I think are important (-:
A few rules I used in this list:
Everything can be understood by a typical undergraduate college student.
If multiple numbers have a shared property, that property is described under one "representative" number with that property. I try to choose the smallest representative example that is not also cited for another property.
When a given number has more than one type of property, the properties are listed in this order:
1. Purely mathematical properties unrelated to the use of base 10 (example: 137 is prime.)
2. Base-10-specific mathematical properties (example: 137 is prime; remove the "1": 37 is also prime; remove the "3": 7 is also prime)
3. Things related to the physical world but outside human culture (example: 137 is close to the reciprocal of the fine-structure constant, once thought to be exact but later found to be closer to 137.036...)
4. All other properties (example: 137 has often been given a somewhat mystical significance due to its proximity to the fine-structure constant, most famously by Eddington)
Due to blatant personal bias, I only give one entry each to complex, imaginary, negative numbers and zero, devoting all the rest (about 25 pages) to positive real numbers. I also have a bit of an integer bias but that hasn't had such a severe effect. A little more about complex numbers, quaternions and so on, is here.
This page is meant to counteract the forces of Munafo's Laws of Mathematics. If you see room for improvement, let me know!
(1+i)/√2 = 0.707106... + 0.707106...i
One of the square roots of i.
When I was about 12 years old, my step-brother gave me a question to pass the time: If i is the square root of -1, what is the square root of i?. I had already seen a drawing of the complex plane, so I used it to look for useful patterns and noticed pretty quickly that the powers of i go in a circle. I estimated the square root of i to be about 0.7 + 0.7i.
I can't remember why I didn't get the exact answer: either I didn't know trigonometry or the Pythagorean theorem, or how to solve multivariable equations, or perhaps was just tired of doing maths (I had clearly hit on Euler's formula and there's a good chance that contemplating the powers of 1+i would have led me all the way through base-i logarithms and De Moivre's formula to the complex exponential function).
But you don't need that to find the square root of i. All you need to do is treat i as some kind of unknown value with the special property that any i2 can be changed into a -1. You also need the idea of solving equations with coefficients and variables, and the square root of i is something of the form "a+bi". Then you can find the square root of i by solving the equation:
(a+bi)2 = i
Expand the (a+bi)2 in the normal way to get a2 + 2abi + b2i2, and then change the i2 to -1:
a2 + 2abi - b2 = i
Then just put the real parts together:
(a2-b2) + 2abi = i
Since the real coordinate of the left side has to be equal to the real coordinate of the right, and likewise for the imaginary coordinates, we have two simultaneous equations in two variables:
a2-b2 = 0
2ab = 1
From the first equation a2-b2 = 0, we get a=b; substituting this into the other equation we get 2a2 = 1, and a=±1/√2 and this is also the value of b. Thus, the original desired square root of i is a+bi = (1+i)/√2 (or the negative of this).
(This is the only complex number with its own entry in this collection, mainly because it's the only one I've had much interest in; see the "blatant personal bias" note above :-).
The unit of imaginary numbers, and one of the square roots of -1.
(This is the only imaginary number with its own entry in this collection, mainly because it stands out way above the rest in notability. In addition, non-real numbers don't seem to interest me much...)
This number, which is the "nucleus" of the period-3 "island" R2F(1/2B1)S in the Mandelbrot set, has the curious property that the Mandelbrot iteration formula fails to produce a sequence in which each term has a prime factor in the numerator that did not occur earlier in the sequence:
0, -7/4, 21/16, -7/256, -114639/65536, ...
which when factored is:
0, -7/22, 3×7/24, -7/28, -3×7×53×103/216, ...
The -7/256 term has just a 7 in the numerator, which does not introduce a new prime factor.
It is known that all integers (except -2, -1, and 0) the Mandelbrot iteration gives sequences with new primes each time. It also seems to hold for almost all fractions; in fact -7/4 is the only known exception.
Numberphile has a video about this (which starts with the similar property of 63).
Negative Numbers
-1 is the "first" negative number, unless you define "first" to be "lowest"...
In "two's complement" representation used in computers to store integers (within a fixed range), numbers are stored in base 2 (binary) with separate base-2 digits in different "bits" of a register. Negative numbers have a 1 in the highest position of the register. The value of -1 is represented by 1's in all positions, which is the same as what you'd get if you wrote a program to compute
1 + 2 + 4 + 8 + 16 + ...
and let it go long enough to overflow.
As it turns out, that series sum can be treated as an example of the general series sum
1 + x + x2 + x3 + x4 + ...
As discussed in the entry for 1/2, the sum is equal to 1/(1-x), but that is valid only when |x| < 1. However if we let x=2 and use the formula anyway, we get 1/(1-x) = 1/(1-2) = -1, which is the same as the two's complement interpretation.
(I do not have many entries for negative numbers, as they do not interest so much. Perhaps I still relate to numbers in terms of counting things like "the 27 sheep on that hill" or "the 40320 permutations of the Loughborough tower bells".)
The (in)famous sum of the positive integers:
1 + 2 + 3 + 4 + 5 + 6 + 7 + ... = 1/12
In the 19th century, new techniques (Cesaro, Abel) were developed to tame some of the infinite series sums that do not converge normally. Examples are shown in the entries for 1/4 and 1/2. But these techniques alone are not enough to handle the infinite series sum:
C = 0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + ...
This sum diverges monotonically (increases towards infinity, without ever taking a step in the negative direction) and Cesaro/Abel will not work.
Euler had to deal with it when performing analytic continuation on what is now called the Riemann zeta function:
Zeta(s) = 1-s + 2-s + 3-s + 4-s + ...
Euler had s = -1, which gives Zeta(s) = 1 + 2 + 3 + 4 + ... Euler's approach was to express it as a linear combination of itself with an existing Cesaro- or Abel-summable series, namely the 1-2+3-4+...=1/4 series, but by Euler's considerably easier diffentiation method:
C = 1 + 2 + 3 + 4 + 5 + 6 + 7 + ...
= 1 + (4-2) + 3 + (8-4) + 5 + (12-6) + 7 + ...
= 1 - 2 + 3 - 4 + 5 - 6 + 7 + ... + 4 (1 + 2 + 3 + ...)
Cesaro/Abel and Euler's methods both give a sum 1/(1+1)2 = 1/4 for the 1-2+3-4+5-... part; so we have
C = 1/4 + 4C
-3C = 1/4
C = -1/12
Numberphile have videos on this, from 2014, 2015, and 2024.
The value of the Riemann Zeta function with argument of -1 is -1/12. As described by John Baez100:
The numbers 12 and 24 play a central role in mathematics thanks to a series of "coincidences" that is just beginning to be understood. One of the first hints of this fact was Euler's bizarre "proof" that
1 + 2 + 3 + 4 + ... = -1/12
which he obtained before Abel declared that "divergent series are the invention of the devil". Euler's formula can now be understood rigorously in terms of the Riemann zeta function, and in physics it explains why bosonic strings work best in 26=24+2 dimensions.
Baez, at the end of his "24" lecture, indicates that the significance of 24 is connected to the fact that there are two ways to construct a lattice on the plane with rotational symmetry: one with 4-fold rotational symmetry and another with 6-fold rotational symmetry — and 4×6=24. A connection between zeta(-1)=-1/12 and symmetry of the plane makes more sense in light of how the Zeta function is computed for general complex arguments. Also, the least common multiple of 4 and 6 is 12.
See also the zeta values 1.202056... and 1.644934....
Ramanujan's -1/12 sum
Srinivasa Ramanujan also explained 1 + 2 + 3 + 4 + ... = -1/12, but in a more general way than Euler. He used a new analytic continuation of the Riemann zeta function.
In Ramanujan's 1913 letter to G.H. Hardy, the as-yet-undiscovered Indian mathematicical genius listed many of his discoveries and derivations. In section XI he stated:
I have got theorems on divergent series, theorems to calculate the convergent values corresponding to the divergent series, viz.
1 - 2 + 3 - 4 + ... = 1/4,
1 - 1! + 2! - 3! + ... = .596... ,
1 + 2 + 3 + 4 + ... = -1/12,
13 + 23 + 33 + 43 + ... = 1/120,
Theorems to calculate such values for any given series (say: 1 - 12 + 22 - 32 + 42 - 52 + ...), and the meaning of such values.
In modern notation we append (ℜ) to the end of such a series sum, to signify Ramanujan summation:
1 - 1! + 2! - 3! + ... = .596... (ℜ)
The Ramanujan sum defines a function f(x) whose values for integer x are the terms in the series being summed. Then
1 + 2 + 3 + 4 + ... n (ℜ)
= Sigmak=1n f(k)
= Integralx=0n f(x) + Sigmak=1∞ Bk/k!
(f(k-1)(n)-f(k-1)(0)) + R
where Bk is the kth Bernoulli number, and f(k-1) is the (k-1)th derivative of f(). Hardy and Ramanjuan considered just the parts of this that do not depend on n:
Sigmak=1∞ Bk/k! (-f(k-1)(0))
For a converging series, f(x) would approach a limit as x approaches infinity, and this would give a value that is equal to the sum of the infinite series. In our case the f(x) diverges, and the series sum is infinite, but this Hardy-Ramanujan sum is not. f(0) is 0, and the 1st derivative is constant f'(x) = 1, and all higher derivatives are zero, so it reduces to just
B2/2! (-1)
B2 (the second Bernoulli number) is 1/6, so we get -1/12.
The word "zero" is the only number name in English that can be traced back to Arabic (صِفر ʂifr "nothing", "cipher"; which became zefiro in Italian, later contracted by removing the fi). The word came with the symbol, at around the same time the western Arabic numerals came to Europe.44,105
The practice of using a symbol to hold the place of another digit when there is no value in that place (such as the 0 in 107 indicating there are no 10's) goes back to 5th-century India, where it was called shunya or Śūnyatā107.
(This is the only zero number with its own entry in this collection, mainly because a field can have only one additive identity.)
This is the Planck time in seconds, according to the latest CODATA recommended values 50; it is related to quantum mechanics. According to the Wikipedia article Planck time, "Within the framework of the laws of physics as we understand them today, for times less than one Planck time apart, we can neither measure nor detect any change". One could think of it as "the shortest measurable period of time", and for any purpose within the real world (if one believes in Quantum mechanics), any two events that are separated by less than this amount of time can be considered simultaneous.
It takes light (traveling at the speed of light) this long to travel one Planck length unit, which itself is much smaller than a proton, electron or any particle whose size is known.
See also 1.416...×1032.
This is the Planck length in meters; it is related to quantum mechanics. The best interpretation for most people is that the Planck length is the smallest measurable length, or the smallest length that has any relevance to events that we can observe. This uses the CODATA 2022 value50. See also 5.391×10-44 and 299792458.
The "reduced" Planck constant in joule-seconds, from CODATA 2022 recommended values50. By the 2019 revision of the SI the non-reduced Planck constant was defined as a constant, making this a constant also.
This is the Planck constant in joule-seconds, from CODATA 2022 recommended values50. This gives the proportion between the energy of a photon and its wavelength.
As of 1st May 2019, as part of the 2019 revision of the SI, it was defined to be exactly this value, in order to define the kilogram in terms of observable properties of nature. The definition reads:
The kilogram, symbol kg, is the SI unit of mass. It is defined by taking the fixed numerical value of the Planck constant h to be 6.62607015×10-34 when expressed in the unit J s, which is equal to kg m2 s-1, where the metre and the second are defined in terms of c and δνCs.
where c is the speed of light by the existing (since 1967) definition (see 299792458) and δνCs is the unperturbed ground-state hyperfine transition frequency of Caesium-133 (see 9192631770).
The mass of an electron in kilograms, from CODATA 2022 recommended values50. See also 206.768...
The mass of a proton in kilograms, from CODATA 2022 recommended values50.
The mass of a neutron in kilograms, from CODATA 2022 recommended values50.
The approximate time (in seconds) it takes light to traverse the width of a proton.
Value of the Boltzmann constant by the old (pre-2019) definition, as given in CODATA 2014 50. This value was based on experimental observations and also upon the definition of the Kelvin, which was determined by measuring the temperature of the triple point of water and defining the Kelvin so that the triple point temperature comes out to 273.16 K. For the current (2019 and later) definition see 1.380649×10-23.
The Boltzmann constant (in Joules per degree Kelvin) by the 2019 redefinition, which reads:
The kelvin, symbol K, is the SI unit of thermodynamic temperature. It is defined by taking the fixed numerical value of the Boltzmann constant k to be 1.380649×10-23 when expressed in the unit J K-1, which is equal to kg m2 s-2 K-1, where the kilogram, metre and second are defined in terms of h, c and δνCs.
where h is the Planck constant by the new definition (see 6.62607015×10-34), c is the speed of light by the existing (since 1967) definition (see 299792458) and δνCs is the unperturbed ground-state hyperfine transition frequency of Caesium-133 (see 9192631770).
The quantum of electric charge in coulombs (one third of the electron charge), based on CODATA 2022 recommended values50. As part of the 2019 revision of the SI, it was defined to be exactly this value. Protons, electrons and quarks all have charges that are a (positive or negative) integer multiple of this value.
The elementary charge or "unit charge", the charge of an electron in coulombs, from CODATA 2022 recommended values50. This is no longer considered the smallest quantum of charge, now that matter is known to be composed largely of quarks which have charges in multiples of a quantum that is exactly 1/3 this value.
As of the 1st May 2019, (see 2019 revision of the SI) the International System of Units (SI) was updated to define its seven base units in a way that defines all seven of them in terms of observable properties of nature, which are given arbitrary numerical values in terms of the base units:
The ampere, symbol A, is the SI unit of electric current. It is defined by taking the fixed numerical value of the elementary charge e to be 1.602176634×10-19 when expressed in the unit C, which is equal to A s, where the second is defined in terms of δνCs.
where δνCs is the unperturbed ground-state hyperfine transition frequency of Caesium-133 (see 9192631770).
As a result of the 2019 change, the elementary charge is no longer measured; it is defined to be exactly 1.602176634×10-19 coulombs; in other words, the coulomb is now defined in terms of the elementary charge (see 6.2415...×1018).
1.75×10-15 (size of the proton)
Approximate "size" of a proton71, in meters (based on its "charge radius" of 0.875 femtometers). "Size" is a pretty vague concept for particles, and different definitions are needed for different problems. See 1040.
The vacuum permittivity constant in farads per meter, using the old (pre-2019) definitions of the vacuum permeability (see 4π/107) and the (still current) definition of the speed of light (see 299792458). In older times this was called the "permittivity of free space". Due to a combination of standard definitions, notably the exact definition of the speed of light, this constant is exactly equal to 107/(4 π 2997924582) = 625000/22468879468420441π farads per metre.
In 2019 and later, the vacuum permittivity is something needing to be computed based on measurement. The greatest uncertainty contributing to its value is the measurement of the fine structure constant.
The gravitational constant in cubic meters per kilogram second squared, from CODATA 2022 recommended values50. This is one of the most important physical constants in physics, notably cosmology and efforts towards unifying relativity with quantum mechanics. It is also one of the most difficult constants to measure. See also 1.32712442099(10)×1020.
The Planck mass in kilograms, using CODATA 2014 values. The Planck mass is related to the speed of light, the Planck constant, and the gravitational constant by the formula Mp = √hc/2πG.
The constant 4π/107 that appears in the old (pre-2019) definition of the "magnetic constant" or vacuum permeability. It is related to the old definition of ampere, which stated that if exactly one ampere of current flows in two straight parallel conductors of infinite length 1 meter apart, the force produced would be 2×10-7 newton per meter of length. This derives from an older definition stating that a similar setup with the wires one centimetre apart would produce a force of 2 dynes per centimetre of length (one dyne is 10-5 newtons).
The fine-structure constant, as given by CODATA 2022 recommendations (see 50). The "(11)" is the error range. See the 137.035... page for history and details.
Here are a few "approximations" involving multiples of 1/127:
e/π = 0.865255... ≈ 110/127 = 0.866141...
√3 = 1.732050... ≈ 220/127 = 1.732283...
π = 3.141592... ≈ 399/127 = 3.141732...
√62 = 7.874007... ≈ 1000/127 = 7.874015...
eπ = 23.140692... ≈ 2939/127 = 23.141732...
There are a few more for 1/7. The √62 coincidence is discussed in the √62 entry, and the π and eπ ones go together (see eπ).
1/100, or "one percent".
0.01671123 (eccentricity of Earth's orbit)
This is the eccentricity of the orbit of the Earth-Moon barycentre at epoch J2000; the value is currently decreasing at a rate of about 0.00000044 per year, mostly due to the influence of other planets. The Moon is massive enough and far enough to shift the Earth itself a few thousand km away from the barycentre. See also 0.054900.
The version of the Gaussian gravitational constant computed by Simon Newcomb in 1895 (see 0.01720209895 for explanation).
The "Gaussian gravitational constant" k, as originally calculated by Gauss, related to the Gaussian year Δt by the formula Δt = 2π/k. The value was later replaced by the Newcomb's smaller value 0.01720209814, but in 1938 (and again in 1976) the IAU adopted the original Gauss value.
See also 354710.
0.054900 (eccentricity of Moon's orbit)
Mean eccentricity of the Moon's orbit — the average variation in the distance of the Moon at perigee (closest point to the Earth) and apogee. Due to the influence of the Sun's gravity the actual eccentricity varies a large amount, going as low as about 0.047 and as high as about 0.070; also the ellipse precesses a full circle every 9 years (see 27.554549878). The eccentricity is greatest when the perigee and apogee coincide with new and full moon. At such times the Moon's distance varies by a total of 14%, and its apparent size (area in sky) varies by 30% when the size at apogee is compared to the size at perigee. This means that the brightness of the full moon varies by 30% over the course of the year. In 2004 the brightest full moon was the one on July 2nd; due to the orbit's precession the brightest full moon in 2006 was a couple months later, Oct 6th.
This change in size is a little too small for people to notice from casual observation (except in solar eclipses, when the Moon sometimes covers the whole sun but at other times produces an annular eclipse). But the eccentricity is large enough to cause major differences in the Moon's speed moving through the sky from one day to the next. When the Moon is near perigee it can move as much as 16.5 degrees in a day; when near apogee it moves only 12 degrees; the mean is 13.2. The cumulative effect of this is that the moon can appear as much as 22 degrees to the east or west of where it would be if the orbit were circular, enough to cause the phases to happen as much as 1.6 days ahead of or behind the prediction made from an ideal circular orbit. It also affects the libration (the apparent "wobbling" of the Moon that enables us to see a little bit of the far side of the moon depending on when you look).
See also 0.01671123.
This is the lowest value of z for which the infinite power tower
zzzzz...
converges to a finite value (and the value it converges to is 1/e). The highest value for which such a power-tower converges is 1.444667...; see that entry for more.
See also 0.692200....
See -1/12.
0.11494204485329620070104015746959...
This is the Kepler–Bouwkamp constant, related to a geometrical construction of concentric inscribed circles and polygons. Start with a unit circle (a circle with radius 1). Inscribe an equilateral triangle inside the circle, then inscribe a circle inside the triangle. The radius of the smaller circle will be cos(π/3) = 1/2. Now inscribe a square inside that circle, and a circle inside the square; this even smaller circle has radius cos(π/3)×cos(π/4) = √1/8. Continue inscribing with a pentagon, hexagon, and every successive regular polygon. The circles get smaller but they do not go all the way down to zero; the limit is this number, about 10/87.
The fraction 1/7 is the simplest example of a fraction with a repeating decimal that has an interesting pattern. See the 7 article for some of its interesting properties.
Reader C. Lucian points out that many of the well-known constants can be approximated by multiples of 1/7:
gamma = 0.5772156... ≈ 4/7 = 0.571428...
e/π = 0.865255... ≈ 6/7 = 0.857142...
√2 = 1.414213... ≈ 10/7 = 1.428571...
√3 = 1.732050... ≈ 12/7 = 1.714285...
e = 2.7182818... ≈ 19/7 = 2.714285...
π = 3.1415926... ≈ 22/7 = 3.142857...
eπ = 23.140692... ≈ 162/7 = 23.142857...
These are mostly all coincidences without any other explanation, except as noted in the entries for √2 and eπ. See also 1/127.
0.1868131868131... = 17/91 (FRACTRAN)
The first fraction in Conway's FRACTRAN program ([154] page 147) that finds all the prime numbers. The complete program is 17/91, 78/85, 19/51, 23/38, 29/33, 77/29, 95/23, 77/19, 1/17, 11/13, 13/11, 15/2, 1/7, 55/1. To "run" the program: starting with X=2, find the first fraction N/D in the sequence for which XN/D is an integer. Use this value NX/D as the new value of X, then repeat. Every time X is set to a power of 2, you've found a prime number, and they will occur in sequence: 22, 23, 25, 27, 211 and so on. It's not very efficient though — it takes 19 steps to find the first prime, 69 for the second, then 281, 710, 2375 ... (Sloane's A7547).
0.20787957635... = e-π/2 = i i
This is e-π/2, which is also equal to i i. (Because eix = cos(x) + isin(x), eiπ/2=i, and therefore i i = (eiπ/2)i = ei2π/2 = e-π/2 .)
The Cesaro sum of the alternating-diverging infinite series sum:
1 - 2 + 3 - 4 + 5 - 6 + 7 - ...
which can be used to derive the Euler/Ramanujan "infamous" sum 1 + 2 + 3 + 4 + ... = -1/12.
The first-order Cesaro method is illustrated in the entry for 1/2. Here we'll apply the method twice. We start with the terms of the infinite series:
A-1(n) : 1, -2, 3, -4, 5, -6, 7, ...
This has the partial sums:
Ao(n) : 1, -1, 2, -2, 3, -3, 4, ...
These diverge and are unbounded both above and below. The sum of the first n terms of that series is:
A'(n) : 1, 0, 2, 0, 3, 0, 4, ...
The average of the first n terms of Ao(n) is A'(n)/n:
(C,1)-sum = A'(n)/n : 1, 0, 2/3, 0, 3/5, 0, 4/7, ...
This is not converging but offers hope in that (like 1-1+1-...) it manages to at least remain bounded from above as well as below. The even terms are all 0 while the odd terms approach 1/2.
Let's take successive averages of this sequence: the Cesaro sum of the Cesaro sum. The sum of the first n terms of the above "(C,1)-sum" is
1, 1, 5/3, 5/3, 34/15, 34/15, 298/105, ...
and successive averages are just these over n:
1, 1/2, 5/9, 5/12, 34/75, 34/90, 298/735, ...
which converge on 1/4, though it may be a bit tough to see here. This isn't actually how Cesaro defined the 2rd order method. Instead, he put the sum of the first n terms of A'(n) in the numerator:
A''(n) : 1, 1, 3, 3, 6, 6, 10, ...
and the binomial coefficients nC2 (the triangular numbers), called "E''(n)", in the denominator:
E''(n) : 1, 3, 6, 10, 15, 21, 28, 35, ...
The second-order averages by Cesaro's method are:
(C,2)-sum = A''(n)/C(n,2) : 1, 1/3, 3/6, 3/10, 6/15, 6/21, 10/28, ...
and these also converge on 1/4. Adding this way makes it easier to see because e.g. for even n we can let h be n/2 and we get:
A''(n)/C(n,2) = hC2 / 2hC2
= (h(h-1)/2) / (2h(2h-1)/2)
= (h2-h)/(4h2-2h)
= (1/2) (2h2-h-h2)/(2h2-h)
= (1/2) ((2h2-h)/(2h2-h) - h2/(2h2-h))
= 1/2 - 1/2 (h2/(2h2-h))
The part "h2/(2h2-h)" clearly converges on 1/2, so the whole thing converges to 1/2 - 1/4.
This sum of 1/4 appears as "1/(1+1)2" in Ramanujan's notebook. That can be derived by noting that 1-1+1-1+1-1+... has the 1st-order Cesaro sum 1/2, and then doing this:
(1 - 1 + 1 - 1 + 1 - ...)2
= (1 - 1 + 1 - 1 + 1 - ...)×(1 - 1 + 1 - 1 + 1 - ...)
= 1 + (-1×1 + 1×-1) + (1×1 + -1×-1 + 1×1)
+ (-1×1 + 1×-1 + -1×1 + 1×-1) + ...
= 1 - 2 + 3 - 4 + ...
So the sum of 1 - 2 + 3 - 4 + 5 - 6 + 7 - ... must be the square of the sum of 1 - 1 + 1 - 1 + 1 - ..., which is the square of 1/2, which is 1/4.
There is another, perhaps easier, way to get the same answer. Start with this infinite series sum and assume it has a value, here called C:
C = 1 + x + x2 + x3 + x4 + ...
Multiply through by x:
Cx = x + x2 + x3 + ...
Subtract the second from the first:
C - Cx = 1
C(1-x) = 1
C = 1/(1-x)
If x is something like 1/2, it's easy to see that the sum 1 + 1/2 + 1/4 + 1/8 + ... is 2, and 1/(1-x) = 1/(1-1/2) is also 2, so the derivation is valid. But if x were, say, -1, then we'd get 1 - 1 + 1 - 1 + 1 - ... = 1/2, which is discussed in the entry for 1/2. Euler didn't worry about strict convergence and just went ahead with:
1 + x + x2 + x3 + x4 + ... = 1/(1-x)
Let's differentiate both sides!
1 + 2x + 3x2 + 4x3 + ... = 1/(1-x)2
If x=-1 we have the desired sum:
1 - 2 + 3 - 4 + ... = 1/(1-(-1))2
and again the answer is 1/4.
See also 3.732050
0.288788095086602421278899721929... = 1/2 × 3/4 × 7/8 × 15/16 × 31/32 × ... × 1-2-N × ...
This is an infinite product of (1-2-N) for all N. This is also the product of (1-xN) with x=1/2. Euler showed that in the general case, this infinite product can be reduced to the much easier-to-calculate infinite sum 1 - x - x2 + x5 + x7 - x12 - x15 + x22 + x26 - x35 - x40 + ... where the exponents are the pentagonal numbers N(3N-1)/2 (for both positive and negative N), Sloane's A1318.30
0.329239474231204... = acosh(sqrt(2+sqrt(2+4))/2) = ln(2+√3)/4
This is Gottfried Helms' Lucas-Lehmer constant "LucLeh"; see 1.38991066352414... for more.
1/3 is the simplest non-dyadic rational, and the simplest with a non-terminating decimal in base 10.
1/3 is the "Ramanujan sum" of the non-converging infinite series sum of -2n:
1 - 2 + 4 - 8 + 16 - 32 + ...
Even though we're not allowed to, we could try to apply the series sum formula:
1 + x + x2 + x3 + ... = 1/(1-x)
which converges the normal way only when -1 < x < 1. If we do this, we'd have x = -2 and the sum would be 1/(1-(-2)) = 1/3.
In the Secretary problem, also called the "fiancée", "sultan's dowry", "fussy suitor", or "googol" problem, an interviewer is presented with a number of candidates for a job, one at a time, and can only select one. We imagine that they can somehow appriase a candidate as being better or worse than any particular candidate that was seen earlier. If they pass down a candidate, they cannot go back to that candidate later; and once the choice is made, they cannot choose a subsequent one instead. The number of candidates is known in advance. What is the best strategy for maximising the chances of ending up with the best candidate, and what is the probability of ending up with the best candidate if they use that strategy?
The optimal strategy is to pass on the first 1/e candidates, or about 37%; and then choose the next one that comes along that is better than those first 37% (or if they get all the way to the final candidate, choose that one.) If this strategy is used, there is a 1/e probability they will end up with the best one.
This is "Artin's Constant", the product (1-1/2)(1-1/6)(1-1/20)...(1-1/(p(p-1))) for all prime p. It relates to the conjecture regarding the "density" of primes p for which 1/p has a as a primitive root, where a meets the conditions of OEIS sequence A85397. This includes 10, meaning that about 30% of primes have a reciprocal with a decimal expansion that repeats every p-1 digits; the first two are 7 and 17.
Curiously, the integral
∫0..∞cos(2x)∏1..•cos(x/n)dx
has a value that is very close to, but not exactly, π/8. From Bernard Mares, Jr. via Bailey et al. [197]; more on MathWorld at Infinite Cosine Product Integral.
See also 0.3926990816987.
If you take a string of 1's and 0's and follow it by its complement (the same string with 1's switched to 0's and vice versa) you get a string twice as long. If you repeat the process forever (starting with 0 as the initial string) you get the sequence
011010011001011010010110...
and if you make this a binary fraction 0.0110100110010110...2 the equivalent in base 10 is 0.41245403364..., and is called the Thue-Morse constant or the parity constant. Its value is given by a ratio of infinite products:
4 K = 2 - PRODUCT[22n-1] / PRODUCT[22n]
= 2 - (1 × 3 × 15 × 255 × 65535 × ...)/(2 × 4 × 16 × 256 × 65536 × ...)
The Cesaro sum of the simplest Cesaro-summable infinite series sum:
1 - 1 + 1 - 1 + 1 - 1 + 1 - ...
The Cesaro sum technique is a generalisation of the definition of an infinite series sum as the limit of its partial sums. To illustrate the principle, let's consider an infinite sum that actually does converge in the normal way:
1 + 1/2 + 1/4 + 1/8 + ...
this has the partial sums:
1, 3/2, 7/4, 15/8, ...
which can easily be seen (and proven, by mathematical induction) to converge to 2. Cesaro considered the series of averages (arithmetic means) of the first N partial sums:
1, (1 + 3/2)/2, (1 + 3/2 + 7/4)/3, (1 + 3/2 + 7/4 + 15/8)/4, ..
which is:
1, 5/4, 17/12, 49/32, 129/80, 321/128, 769/448, ...
which also converges on 2, though more slowly. This technique of averaging the first n partial sums can yield an answer for infinite series whose partial sums taken individually so not converge. Start with:
1 - 1 + 1 - 1 + 1 - 1 + 1 - ...
The partial sums are:
1, 0, 1, 0, 1, 0, 1, ...
This doesn't converge, but let's take the average of the first n of these. The sums of the first n of these (for n=1, 2, 3, ...) are:
1, 1, 2, 2, 3, 3, 4, ...
So the average of the first n partial sums are:
1, 1/2, 2/3, 1/2, 3/5, 1/2, 4/7, ...
which converges on 1/2. See 1/4 for an example of 2rd order Cesaro summation, and -1/12 to see Ramanujan's extension.
Ramanujan's notebook, when discussing the -1/12 series, uses "1/(1+1)2", which suggests that he viewed the sum 1 - 1 + 1 - 1 + 1 - 1 + 1 - ... to be "1/(1+1)". This can be derived from the generalisation of the series sum:
1 + x + x2 + x3 + ... = 1/(1-x)
which converges the normal way only when |x| < 1; but if we consider x = -1 we'd get "1 - 1 + 1 - 1 + 1 - 1 + 1 - ... = 1/(1-x) = 1/(1+1)". So the value 1/2 can be "justified" in two ways.
This is the integral of sin(1/*x), from 0 to 1. Mathematica or Wolfram Alpha will give more digits: 0.5040670619069283719898561177411482296249850282126391708714331675557800743661836160517915604457297012...
0.5294805... + 3.342716... i (Hankins' zillion)
A reader[216] suggested to me the idea that some people might define "zillion" as "a 1 followed by a zillion zeros". This is kind of like the definition of googolplex but contradicts itself, in that no matter what value you pick for X, 10X is bigger than X.
However, this is actually only true if we limit X to be an integer (or a real number). If X is allowed to be a complex number, then the equation 10X=X has infinitely many solutions.
Using Wolfram Alpha[230], put in "10^x=x" and you will get:
x ≈ -0.434294481903251827651 Wn(-2.30258509299404568402)
with a note describing Wk as the "product log function", which is related to the Lambert W function (see 2.50618...). This function is also available in Wolfram Alpha (or in Mathematica) using the name "ProductLog[k, x]" where k is any integer and x is the argument. So if we put in "-0.434294481903251827651 * ProductLog[1, -2.30258509299404568402]", we get:
0.529480508259063653364... - 3.34271620208278281864... i
Finally, put in "10^(0.529480508259063653364 - 3.34271620208278281864 * i)" and get:
0.52948050825906365335... - 3.3427162020827828186... i
If we used -2 as the initial argument of ProductLog[], we get 0.5294805+3.342716i, and in general all the solutions occur as complex conjugate pairs. Other solutions include x=-0.119194...±0.750583...i and x=0.787783...±6.083768...i.
In light of the fact that the -illion numbers are all powers of 1000, another reader suggested[221] that one should do the above starting with 10(3X+3)=X. This leads to similar results, with one of the first roots being:
-0.88063650680345718868... - 2.10395020077170002545... i
The odds of losing a game of chance. Flip a coin: if you get heads, your score increases by π, if you get tails, your score diminishes by 1. Repeat as many times as you wish — but if your score ever goes negative, you lose. Assuming the player keeps playing indefinitely (motivated by the temptation of getting an ever-higher score), what are the odds of losing?
The answer is given by a series sum: 1/2 + 1/25 + 4/29 + 22/213 + 140/217 + 969/221 + 7084/225 + 53820/229 + 420732/234 + ..., (numerators in Sloane's A181784) which adds up to 0.5436433121...
A more sophisticated analysis using rational numbers like 355/113 converges on the answer more quickly, giving 0.54364331210052407755147385529445... (see [205]).
More on my page on sequence A181784.
See also 368.
0.567143290409783872999968662210355549753815787186512508135131... (the Omega constant)
This is the Omega constant, which satisfies each of these simple equations (all equivalent):
|
Thus it is sort of like the golden ratio. In the above equations, if e is replaced with any number bigger than 1 (and "ln" by the corresponding logarithm) and you get another "Omega" constant. For example:
if 2x=1/x, then x=0.6411857445...
if πx=1/x, then x=0.5393434988...
if 4x=1/x, then x=1/2
if 10x=1/x, then x=0.3990129782...
if 27x=1/x, then x=1/3
if 10000000000x=1/x, then x=1/10
(the Euler-Mascheroni constant)
This is the Euler-Mascheroni constant, commonly designated by the Greek letter gamma. It is defined in the following way. Consider the sum:
Sn = 1 + 1/2 + 1/3 + 1/4 + 1/5 + ... + 1/n
The sequence starts 1, 1.5, 1.833333..., 2.083333..., etc. As n approaches infinity, the sum approaches ln(n) + gamma. Numberphile has a video about this constant: The mystery of 0.577.
Here are some not-particularly-significant approximations to gamma:
1/(√π - 1/25) = 0.5772159526...
gamma = 0.5772156649...
1/(1+ 1/√10)2 = 0.5772153925...
One of the infinite sums in Ramanujan's 1913 letter to G.H. Hardy, section XI:
1 - 1! + 2! - 3! + ... = .596... ,
see -1/12 for a simpler example.
this sum diverges, but a partial sum can be contemplated:
0 + 1 + 2 + ... + n
= SUMi in [0..n] f(i)
(where f(x) = x)
= -f(0)/2 + i INTEGRAL0..∞ (f(it)-f(-it)) / (e2πt - 1) dt
in this specific example we get
-2 INTEGRALv{{0..∞} 1/(e2πt-1) dt
Value of the infinite series sum
1/1 - 1/√2 + 1/√3 - 1/√4 + 1/√5 - ...
It is (1-√2) times the Riemann zeta function of 1/2. More digits: 0.604898643421630370247265914... (Sloane's sequence A113024). Oddly, though the series sum converges to a reasonably small finite value, if you square the series sum:
(1/1 - 1/√2 + 1/√3 - 1/√4 + 1/√5 - ...)2
and sum the terms in the needed order:
1/1 - (1/1×√2 + 1/1×√2)
+ (1/1×√3 + 1/√2×√2 + 1/√3×√1)
- (1/1×√4 + 1/√2×√3 + 1/√3×√2 + 1/√1×1)
+ ...
= 1/1 - (1/√2) + (2/√3 + 1/2) - (2/√4 + 2/√6) + ...
the magnitudes of the parenthesised parts keep growing, so the series sum diverges. However, there clearly is a sum, and technuqies such as Cesaro summation (see the entry for 1/4) can be used to evaluate it and get the proper answer, It is for sums like this that Cesaro summation is really needed. (The case for 1/4 is a bit harder to argue.)
(inverse Golden ratio)
The golden ratio (reciprocal form): see 1.618033....
The Buffon's needle problem involves estimating the probability that a randomly-placed line segment of some given length will cross one of a a set of parallel lines spaced some fixed distance apart. If the length of the line segment is the same as the spacing between lines, the probability is 2/π.
See also 0.773239....
0.692200... = (1/e)(1/e)
This is the lowest point in the function y = xx. See also 1.444667....
The natural logarithm of 2, written "ln(2)". See 69.3147... and 72.
ln(2) is the value of this infinite series sum:
1 - 1/2 + 1/3 - 1/4 + 1/5 - 1/6 + 1/7 - 1/8 + ...
= 1/2 + 1/12 + 1/30 + 1/56 + ...
This is called a "conditionally convergent series" because the series converges if added up in the way shown above, but if you rearrange the terms:
1 + 1/3 + 1/5 + 1/7 + ... - (1/2 + 1/4 + 1/6 + 1/8 + ...)
then you have two series that do not converge and an undefined "infinity minus infinity".
The Rabbit constant
You can create a long string of 1's and 0's by using "substitution rules" and iterating from a small starting string like 0 or 1. If you use the rule:
0 → 1
1 → 10
and start with 0, you get 1, 10, 101, 10110, 10110101, 1011010110110, ... where each string is the previous one followed by the one before that (Sloane's A36299 or A61107). The limit of this is an infinite string of 1's and 0's which you can make this into a binary fraction: 0.1011010110110...2, you get this constant (0.709803... in base 10) which is called the Rabbit Constant. It has some special relationships to the Fibonacci sequence:
- In the iteration described above, the number of digits in each string is the Fibonacci sequence: 1, 1, 2, 3, 5, 8, 13, 21, ...
- Expressed as a continued fraction, the constant is 0 + 1/(20 + 1/(21 + 1/(21 + 1/(22 + 1/(23 + 1/(25 + 1/(28 + ...))))))) where the exponents of 2 are the Fibonacci numbers.
- If you take all the multiples of the Golden Ratio 0.618033 and round them down to integers, you get 1, 3, 4, 6, 8, 9, 11, 12, ...: These numbers tell you where the 1's in the binary fraction are.
If you leave off the first two binary digits (10) you get 110101101101011010110110101..., the bit pattern generated by a Turing machine at the end of the Turing machine Google Doodle. As a fraction (0.1101011...) it is 0.8392137714451.
0.7236067977... = phi/√5 = 1/2 + √1/20
The powers of this number, rounded to the nesrest integer, give the Fibonacci numbers; see phi for more.
Value of x such that x=cos(x), using radians as the unit of angle. You can find the value with a scientific calculator just by putting in any reasonably close number and hitting the cosine key over and over again. Here are a few more digits: 0.7390851332151606416553120876738734040134117589007574649656...26
This is 3 - √5, and is related to a sequence of Grafting numbers found by Matt Parker. With more precision, it is: 0.76393202250021030359082633126872376455938164038847...
Take an odd number of digits after the decimal point, add 1, and you get a Grafting number. For example, 76393+1 = 76394. The sequence of numbers derived this way starts: 8, 764, 76394, 7639321, 763932023, 76393202251, 7639320225003, ...
A fiendishly engaging approximation to the answer to the "infinite resistor network" problem in xkcd 356, which introduced the world to the sport of "nerd sniping". See ries and 0.773239....
0.7732395447351... = 4/π - 1/2
The answer to a fiendishly engaging "infinite resistor network" problem in xkcd 356, which introduced the world to the sport of "nerd sniping" 90. See also 0.636619... and 0.772453....
This number, on an early calculator with 7-segment display, says "hello" when seen upside-down:
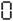


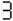
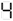 →
→
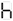


See also 71077345.
This is INTEGRAL0..1 xx dx, which is curiously equal to - SIGMAi..inf (-n)-n, which was proven by Bernoulli. With more digits, it is 0.78343051071213440705926438652697546940768199014... It shares (with 1.291285... the nickname "sophomore's dream".
This is 0.1101011011010110101101101011011010110101101101011010110110... in binary, and is the slightly different version of the Rabbit constant generated by a Turing machine Google Doodle from June 2012. More digits: 0.8392137714451652585671495977783023880500088230714420678280105786051...
0.8507361882018672603677977605320666044113994930...
Decimal value of the "regular paperfolding sequence" 1 1 0 1 100 1 1100100 1 110110001100100 1 1101100111001000110110001100100 ... converted to a binary fraction. This sequence of 1's and 0's gives the left and right turns as one walks along a dragon curve. It is the sum of 82k/(22k+2-1) for all k≥0, a series sum that gives twice as many digits with each additional term.
The square root of 3 divided by 2 occurs in many places, some of them unexpected, including several that are explained in a nice video by Matt Parker. See also 1.618033.
The minimum value of the Gamma function with positive real arguments. The Gamma function is the continuous analogue of the factorial function. This is Gamma(1.461632144968...). (For more digits of both, see OEIS sequences A30171 and A30169.)
This is 1/2 of the square root of π. It is Gamma(3/2), and is sometimes also called (1/2)!, the factorial of 1/2.
See also 0.906402... and 1.329340....
This is (4+4√2)/(5+4√2), and is the best density achievable by packing equal-sized regular octagons in the plane. Notably, it is a bit smaller than 0.906899..., the density achievable with circles.
0.906402477055477077982671288...
This is Gamma(5/4), or "the factorial of 1/4". While some Gamma function values, like 0.886226... and 1.329340..., have simple formulas involving just π to a rational power, this one is a lot more complicated. It is π to the power of 3/4, divided by (√2+4√2), times the sum of an infinite series for an elliptic function.
This is π/12, the density achievable by packing equal-sized circles in a plane. See also 0.906163....
Catalan's constant, which can be defined by:
G = ∫(0,1) [ arctan(x) / x dx ]
or
G = 1 - 1/32 + 1/52 - 1/72 + 1/92 - ...
If you have a 2n × 2n checkerboard and a supply of 2 n2 dominoes that are just large enough to cover two squares of the checkerboard, how many ways are there to cover the whole board with the dominoes? For large n, the answer is closely approximated by
f'n = e4 G n2 / π
0.922276847117579694535372498...
This is the cube root of (5√27 - 5√2). Bill Gosper discovered the following identity, which is remarkable because the left side only has powers of 2 and 3, but the right side has a power of 5 in the denominator 108:
(5√27-5√2)(1/3) = (5√8 5√9 + 5√4 - 5√2 5√27 + 5√3) / 3√25
or in his original form:
(3(3/5)-2(1/5))(1/3) = (- 2(1/5)3(3/5) + 2(3/5)3(2/5) + 3(1/5) + 2(2/5) ) / 5(2/3)
See also 1.554682...
. . . Forward to page 2 . . . Last page (page 25)
Quick index: if you're looking for a specific number, start with whichever of these is closest: 0.065988... 1 1.618033... 3.141592... 4 12 16 21 24 29 39 46 52 64 68 89 107 137.03599... 158 231 256 365 616 714 1024 1729 4181 10080 45360 262144 1969920 73939133 4294967297 5×1011 1018 5.4×1027 1040 5.21...×1078 1.29...×10865 1040000 109152051 101036 101010100 — — footnotes Also, check out my large numbers and integer sequences pages.
This page was written in the "embarrassingly readable" markup language RHTF, and some sections were last updated on 2026 Jan 02.
 s.30
s.30