Notable Properties of Specific Numbers
First page . . . Forward to page 3 . . . Last page (page 25)
Many properties, mostly for trivial reasons (see 3.) Perhaps its most profound3 property is that 13=17=127=...
This is the ratio between 12 "perfect fifths" (an interval in music, a pitch ratio of precisely 3/2) and 7 perfect octaves (a ratio of precisely 2/1).[202] It is called the Pythagorean comma because of the practice in Pythagoras' time of defining all musical intervals (including all the notes on the major scale) as ratios between some power of 2 and some power of 3.
The value is close to the 51st root of 2, however, dividing the octave divided into 51 parts with a note-to-note ratio of 21/51 = 1.0136839... does not make a better musical scale. In the 53 equal temperament scale the "semitone" closely approximates the ratio 312/219.
See also 1.05946....
The ratio between successive pitches on the popular western 12-note "equal temperament" musical scale (see that article for much related history). 21/12 is useful for this purpose because 7 intervals are very close to the "perfect fifth" 3::2 ratio (in other words, 27/12 ≈ 3/2) and because 12 is a manageably small number: it is fairly practical to construct instruments and sheet music notation systems that work with a 12-notes-per-octave system.
See also 1.01364....
The edge-length of the largest square that fits inside a unit cube. To locate the four corners of such a square, start with two adjacent edges of the cube and mark two points that are 3/4 units from the common corner. The distance between the two points is 3√2/4 and the line segment connecting them is one of the edges of the square. The two other points are symmetrically opposite. By symmetry it is clear that they are coplanar so they are the corners of a rectangle; it is easy to show that the other two edges of the rectangle are also of length 3√2/4. The related problem of Prince Rupert's cube concerns cutting a hold in a unit cube through which another unit cube (or a slightly larger cube) can pass.
See also 1.06066017177....
Apéry's constant, or zeta(3). If you pick three positive integers at random, the odds of them having no common divisor are 1 in 1.2020569... It is also the value of any of these infinite sum:
1 + 2-3 + 3-3 + 4-3 + ... = 8/7 [1 + 3-3 + 5-3 + 7-3 + ...] = 4/3 [1 - 2-3 + 3-3 - 4-3 + 5-3 - ...] = 5/2 [1/2 - (2!2)/(4!23) + (3!2)/(6!33) - (4!2)/(8!43) + ...] = 1.202056903159594285399738161511449990764986292...
It is called Apéry's constant because in 1978 Roger Apéry surprised the mathematical community by showing that it is irrational. There is a great video by Numberphile, Apéry's constant calculated with Twitter. See also 0.0833333... and 1.644934....
This is the limit of the series:
ln(3) = 1.098612...
ln(ln(33)) = 1.192660...
ln(ln(ln(333))) = 1.220795...
The ordinary rules for reducing expressions (like ln(33) = 3×ln(3)) are not enough for figuring out this limit. However, using Hypercalc the limit is pretty easy to find.
To see that there is a well-defined limit, consider the following relationships (these are different from the initial problem, by having an extra exponent of x):
ln(3x) = ln(3) * x
ln(ln(33x)) = ln(ln(3)*3x) = ln(ln(3)) + ln(3)* x
ln[ln(ln(333x))] = ln[ln(ln(3) * 33x)] = ln[ln(ln(3)) + ln(3)*3x]
As x gets larger, approaching infinity, ln(ln(3)) + ln(3)*3x is almost exactly equal to ln(3)*3x, so we have ln[ln(3)*3x] which is ln(ln(3)) + ln(3)* x. Note that is the same as the expression for ln(ln(33x)). The same type of thing happens with ln{ln[ln(ln(3333x))]}.
Going back to the original problem, let x stand for 3333 and put an extra "ln(ln(ln(ln(...)))))" around the whole thing, and you can see that series has a limit.
Now do the same thing, but with one more 3 and one more ln: let x stand for 33333 and add "ln(ln(ln(ln(ln(...)))))" around each term. Again, there is clearly a limit and this limit will differ only a tiny bit from the previous limit.
Now do the same thing yet again with another 3 and another ln, again there will be a limit that differs by an even lesser amount.
This is 1.1112, and happens to also be very close to √Pi-Phi = 1.234325186...
See also 12345654321.
The cube root of two, the subject of a Greek legend.
On the island of Delos, the birthplace of Apollo and Artemis, was an oracle. At one time, when there was a plague in Athens, an emissary went to the oracle to ask what to do. The oracle replied that the plague would cease if the altar to Apollo were doubled in size. The altar was a perfect cube, one cubit on each side. So the people of Athens built a new altar that was a cube two cubits long on each side. But the plague continued, and when asked, the oracle explained that the new altar was eight times as large as the old one. So they built an altar that was two cubits long in one direction, but one cubit in the other two directions, but the plague continued, as the altar was no longer a cube. Apollo was only to be pleased by an exact cube that was twice the volume of the original: 3√2 cubits on each side. (From [154] page 190, paraphrased.)
The task of deriving the length of 3√2 units based on an existing length of 1 unit is called doubling_the_cube, and it is one of the tasks that cannot be performed with straightedge and compass.
1.27323954473516268615107010... = 4/π
4 / π is the value of the rather pretty continued fraction:
4 / π = 1 + ( 1 / ( 2 + ( 32 / ( 2 + ( 52 / ( 2 + ( 72 / ( 2 + ... ))))))
By contrast, the simple continued fraction for π (where all the numerators are 1) has no pattern:
π = 3 + 1 / ( 7 + 1 / (15 + 1 / (1 + 1 / (292 + 1 / (1 + ...)))))
It is also the ratio between the arc-length of a Cycloid and the length of the straight line between cusps. In other words, as the axle of a wheel with radius r travels 2πr, a point on its rim travels 8r, so the ratio is 8r/2πr = 4/π.
1.28242712910062263687534256886979172776768892732500...
The Glaisher-Kinkelin constant
This is the Glaisher-Kinkelin constant, related to the Barnes G-function and the K-function. It appears in these approximations of the G-function and the K-function:
K(n+1) ≈ A nn2/2+n/2+1/12e-n2/4
G(n) ≈ (e1/12/A) nn2/2-1/12(2{pi|)n/2e-3n2/4
This is the infinite sum
1 + 1/22 + 1/33 + 1/44 + 1/55 + . . .
which happens to also be INTEGRAL[0..1] x-x dx :
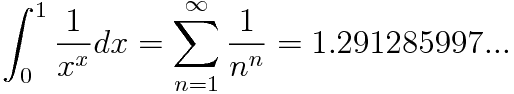
To greater precision, the sum is 1.29128599706266354040728259059560054149861936827... It is sometimes called "the sophomore's dream" in analogy to the false identity "(x+y)n = xn + yn" called "the freshman's dream".
It's also kind of close to ln(3)e = 1.2912987577...[226] but that's just a coincidence.
This is the fractal dimension of the "Apollonian packing", a rather pretty fractal made from circles. The precise value is a little difficult to compute; the most digits I have seen is 1.305686729, but that's probably only accurate up to the "7". To make the fractal, start with three circles that are just touching (tangent to) each other, and with none of the circles inside each other. Now there is exactly one way to add a 4th circle in the space between the three circles so that the new circle is tangent to all three. Then you can add three more smaller circles in the spaces between the 4th circle and two of the original three. As you continue this process indefinitely, you get an Apollonian packing.
(lower bound for Mills' constant)
The lowest value of Mills' constant assuming the Riemann Hypothesis is true. In 1947 W. H. Mills proved that there is a constant K such that, for all values of n, the integer part of K3n is prime. The first 100 digits of the constant are: 1.3063778838630806904686144926026057129167845851567136443680537599664340537668265988215014037011973957...
Here is what you get for the first few values of n:
K3 = 2.229494...
K32 = 11.082031...
K33 = 1361.000001...
K34 = 2521008887.000000...
K35 = 16022236204009818131831320183.000000...
Each of these numbers is the cube of the previous one, and when the fraction is removed the resulting integer is prime. The sequence: 2, 23+3=11, (23+3)3+30=1361, ((23+3)3+30)3+6=2521008887, ... is Sloane's A51254.
It is pretty easy to see that Mills' theorem seems to be true, simply because there are so many primes. For example, start with 3: 33 is 27. There are several primes between 27 and 43=64, of which the first is 29. 293 is 24389 and 303 is 27000 — there are even more primes to choose from this time. Choosing the first available prime each time, we get the sequence 3, 29, 24391, 14510715208481, 3055388613462301256452407743005777548691, .... The constant K in this case would be approximately 3055388613462301256452407743005777548691(1/243)=1.45375086254.... In a similar manner, starting with 5 we get 127, 2048413, 8595132382702380079, 634976584256084664026852011723442922433087739799461233111, ... No matter what prime one starts with, there are plenty of primes to choose from each time and therefore plenty of possible values for Mills' constant.
The difficulty in proving this for certain comes from the fact that it is difficult to prove that there is a prime between any two consecutive cubes. So far that has only been proven for primes up to 106000000000000000000.
See also 1.52469996....
1.324717957244746025960908854...
(the plastic ratio)
The asymptotic limit of the ratio between successive terms of the Perrin and Padovan sequences. It is the only real solution to the simple cubic equation x3=x+1. This is analogous to the relation between the golden ratio and the Fibonacci sequence. See also 1.46557... and 2.414213....
This is 3/4 times the square root of π. It is Gamma(5/2), and is sometimes also called (3/2)!, the factorial of 3/2.
See also 0.906402....
1.38991066352414771791154881... = eln(2+√3)/4 = sqrt(sqrt(2+√3))
This is Gottfried Helms' "ELucLeh" constant, which is e to the power of his LucLeh constant ln(2+√3)/4. As described by Helms [225], it can be used for a "simple" Lucas-Lehmer test of prime numbers p. Specifically, given a prime p, you calculate
ELucLeh2p
then round up to the next-higher integer, then see if the result is divisible by 2p-1. Here are some examples, starting with the calculation of ELucLeh2p:
|
Rounding each of these values up to the next-higher integer, and then checking for divisibility we get:
|
Since 3, 5, and 7 pass the test, that means that 7, 31 and 127 are prime (which is indeed true); since 11 fails that means that 2047 is composite (also true: it is 23×89).
Note that this test seems to indicate that 3 is not a Mersenne prime, which is false. But we can forgive this because the real Lucas–Lehmer primality test only works for "odd primes" p, so the smallest 2p-1 for which it is relevant is when p=3.
Testing p=11 requires at least 300 digits, because ELucLeh211 is about 6.87296×10292 and you need to know the exact integer value that you are testing for divisibility by 211-1. Testing larger primes, including any actual Mersenne prime candidates, requires so many digits that this test method is of no use for "practical" Mersenne prime searching.
The square root of 2, √2, also sometimes called "Pythagoras' constant".
It is the aspect ratio of standard sizes of paper in most of the world (not including the United States) because it enables a half-sheet of paper to have the same aspect ratio as a full sheet. A sheet of the "letter size" A4 has an area of 2-4 square metres.
The continued fraction for √2 is:
√2 = 1 + 1/(2 + 1/(2 + 1/(2 + ... )))
yielding the series of rational approximations:
| 1 | 3 | 7 | 17 | 41 | 99 | 239 | a | c | e | ||
| 1 , | 2 , | 5 , | 12 , | 29 , | 70 , | 169 , | . . . | b , | d , | f |
where each new fraction e/f is computed from the previous ones by the formulas:
e = 2c + a = c + 2d
f = 2d + b = c + d
These two sequences are the Pell numbers and another similarly defined sequence discussed under the entry for 99.
If you multiply each numerator by its denominator you get the series discussed under 204.
The square root of 2 itself must be irrational; it cannot be a ratio of two numbers a/b. A proof of this, and some of the other things mentioned above, are discussed in Numberphile's video Root 2.
Curious math fans may have noticed that the digits of √2, taken in pairs, seem to be all multiples of 7:
√2 = 1.4 14 21 35 62 ...
We have "14" repeated twice, then 3×14/2 = 21, then 5×14/2 = 35. The next one is a bit shy of 63 but maybe that's a fluke.
These patterns of digits, and the recurrence of the ratios 2:2:3:5, is not a coincidence. It results from the fact that 2 times 7 squared equals 98, which is a power of 10 minus 2. (Note also that 2×7 = 14, those first 2 digits, and 14×7=98.)
To see why, we start with
1/98 = 0.010204081632...
a digit pattern featuring powers of 2 which is described in the 998 entry. Now it happens that 0.101 squared is 0.010201 (see 10201). Since 0.010204... is a little bigger than this, it makes sense that its square root should be a little bigger than 0.101:
√1/98 = 0.101015254455...
The sequence (1, 2, 4, 8, 16, ...) has become (1, 1, 1.5, 2.5, 4.375, ...) Now imagine that instead of the square root of 1/98, we're taking the square root of 4/98. Since √4X=2√X, the square root of 4/98 has a very similar digit pattern:
√4/98 = 0.202030508910...
But look at the factors of 4 and of 98: 4=2×2 and 98=2×7×7. So √4/98 = √2/49 = √2 / 7. Therefore √2 is 7 times √4/98:
√2 = 7 √4/98 = 7 × 0.202030508910... = 1.414213562373...
Somewhat related is the fact √98 is close to √100=10, meaning that √2 is close to 10/√49 = 10/7 (mentioned in the entry for 1/7).
For a "bigger" example of repeating digits in a square root see the entry for √62.
See also 1.632526919438....
This is the highest value of the function y = x(1/x), and also the highest value of z for which the infinite power tower
zzzzz...
converges to a finite value (which is e itself). The lowest value for which such a power tower converges is e-e = 0.065988....
Euler discovered that the value xxx... converges to is the solution to the equation y1/y=x. That means that you can solve the equation y1/y=x for y by evaluating xxx... (and if it doesn't converge, then there's no solution to the equation). However, it usually takes a lot of iterations to converge and Newton's Method is faster. This iteration can also be used to find some values of x such that xx=y; see here for details.
See also 0.692200....
An alternative value of Mills' constant based on a sequence of primes beginning with 3. See also 1.52469996....
1.4655712318767680266567312...
(the supergolden ratio)
This is the so-called "Supergolden ratio", in analogy to the golden ratio, because it has similar properties. It is the asymptotic limit of the ratio between successive terms of the Narayana's cows sequence, which is analogous to the relation between the golden ratio and the Fibonacci sequence. It is the only positive real solution to the cubic equation x3=x2+1, similar to the quadratic equation x2=x+1 for the golden ratio.
See also 1.414213... and 2.414213....
This is the area of the Mandelbrot set
The number has been measured statistically based on computers counting the "pixels" in the Mandelbrot set's image. Of such calculations, the most precise to date is that by Thorsten Forstemann, using twin Radeon HD 5970 GPUs with a single 2097152×2097152 grid, giving the estimate 1.5065918849(28), or 1.5065918849 ± 0.0000000028. My own estimate, using multiple grids and slightly randomised values for the arbitrary parameters (grid origin, lattice spacing, etc.) is 1.5065918561(254), or 1.5065918561 ± 0.0000000254.
I'll also note that Cyril Soler conjectured that the value is precisely √6π-1 - e, or 1.5065916514855..., now known to be false. My inverse equation solver shows that such approximations are extremely common.
1.52469996053809435992336357568842116222022362319977121984572...
It is very likely that Mills' theorem is true for the formula K2n and that this is the lowest value of K. If so, then the integer part of K2n is always prime for n>1: 2, 5, 29, 853, 727613, 529420677791, 280286254072681840639693, 78560384222095957698731679318817728959447134363, ... (Sloane's A59784). This depends on the unproven conjecture that there is always a prime between any two consecutive squares. Given the difficulty of proving that there is a prime between consecutive cubes, it seems very unlikely that anyone will ever answer this one way or the other.
1.55468227548210008987023208...
This is π√4, the "πth root of 4", also written 4(1/π). Bill Gosper discovered the following identity 108:
π√4 = LIMIT[n→∞] [ π/(2 tan-1(n)) × π/(2 tan-1(n+1)) × ... × π/(2 tan-1(2n)) ]
See also 0.922276... and 23.140692632779269005....
The solution of xx=2. See also 2.506184... and 56.9612....
Numbers of this type are transcendental, except for cases like xx=27. Clearly, if X is an integer, XX is an integer. It is fairly easy to show that if X is not an integer, XX is irrational. These things together with the Gelfond-Schneider Theorem allow one to show that if XX is an integer, and X is not an integer, then X is transcendental.
π/2 is seen often enough that it is sometimes treated as a constant in its own right, separate from π itself (see also 2π).
The precise ratio between a mile and a kilometer. Because of its proximity to phi, one can use the Fibonacci numbers as a handy mnemonic for conversion: 3 mi ≈ 5 km, 5 mi ≈ 8 km, 8 mi {~=] 13 km, etc. The approximation is better than 1/2 km all the way up to 55 mi ~= 89 km. See also 63241.077088071.
The Golden Ratio, (1+√5)/2, 1.61803398874989..., commonly designated by the Greek letter Φ. It is called the golden ratio because of its use in ancient, classical and Renaissance art and architecture. It is the ratio between the height and width of the so-called "golden rectangle", considered to be more aesthetically appealing than any other rectangle. This was probably the result of the fact that, if you take a golden rectangle and add a square to the longest edge to make a larger rectangle, that larger rectangle will have the same ratio (the rectangles are similar. This is reflected in the relation:
1 + 1/Φ = Φ
or (in numbers):
1 + 1/1.618033... = 1.618033...
The ratio of two consecutive Fibonacci numbers approaches Φ as you go up to higher and higher Fibonacci numbers. This is evident in the Binet formula for Fibonacci numbers:
Fn = (Φn-(1-Φ)n)/√5 = (Φn-((-Φ)-n))/√5
In the numerator, the first part Φn grows exponentially, while the second part (-Φ)-n shrinks rapidly towards zero:
F0 = (Φ0-((-Φ-0)))/√5 = (1-1)/√5 = 0
F1 = (Φ1-((-Φ-1)))/√5 = (1.618...+.618...)/√5 = 1
F2 = (Φ2-((-Φ-2)))/√5 = (2.618...-.381...)/√5 = 1
F3 = (Φ3-((-Φ-3)))/√5 = (4.236...+.236...)/√5 = 2
F4 = (Φ4-((-Φ-4)))/√5 = (6.854...-.145...)/√5 = 3
F5 = (Φ5-((-Φ-5)))/√5 = (11.090...+.090...)/√5 = 5
...
The part coming from (-Φ)-n is always small enough to be less than 1/2 after the division by √5, so the Binet formula can be simplified using the "round()" function which simply means rounding to the nearest integer:
Fn = round(Φn/√5)
For a similar formula using e see 44.
The golden ratio shows up in lots of places in mathematics. Φ or 1/Φ is the solution of the simple equations x2 = x + 1, x2 = 1 - x, 1/x = x + 1, and 1/x = x - 1. Φ, 1/Φ and Φ2 all have the same digits after the decimal point: 1.618033..., 0.618033..., 2.618033... . See also 0.8660254..., 2.414213..., and 4.236067....
It is well-known that there are exponents ab such that a and b are both rational but ab is irrational. For example, the square root of 2, √2, is 21/2 and is irrational. But is there any pair of irrational numbers x and y such that the value xy is rational? It is really easy to show the answer is yes, without finding both values of x and y, and the proof involves the number 1.632526919438... = √2√2, which we'll call q.
If q is irrational, then q√2 equals (√2)2, which is 2 so we have a solution with x=q and y=√2. On the other hand, if q is rational, then the solution is x=y=√2.
Two related facts: there are pairs of rational numbers a and b such that ab=a b (see 3.160493...) and there are pairs of rational a and b such that ab=ba (see 15.438887...). See also 1.559610..., 2.665144..., and 9.080217×10666262452970848503.
zeta(2), or π squared over 6. If you pick two positive integers at random, the odds of them having no common divisor are 1 in 1.644934...
This is the sum of the series:
1/12 + 1/22 + 1/32 + 1/42 + 1/52 + 1/62 + 1/72 + ...
= 1 + 1/4 + 1/9 + 1/16 + 1/25 + 1/36 + 1/49 + ...
and calculating an exact answer for it was an unsolved problem in mathematics for many years. It was called the "Basel problem" after the Swiss city where two of the Bernoullis worked, and it was unsolved from 1644 until 1735 (when Euler solved it). The infinite sum can be shown to be equal to a product:
1/[ (1-1/22)(1-1/32)(1-1/52)(1-1/72) ... (1-1/p2) ... ]
where each of the prime numbers occurs once. We start by giving the sum a name x:
x = 1/12 + 1/22 + 1/32 + 1/42 + 1/52 + 1/62 + ...
then we multiply by 1/22 on both sides:
1/22x = 1/22 + 1/42 + 1/62 + 1/82 + 1/102 + 1/122 + ...
then subtract this from the original equation:
(1-1/22)x = 1/12 + 1/32 + 1/52 + 1/72 + 1/92 + ...
Notice that all the evens are gone and we're just left with the odds. Then we do something similar. Multiply both sides by 1/32:
(1/32)(1-1/22)x = 1/32 + 1/92 + 1/152 + 1/212 ...
and subtract the result from the previous equation:
(1-1/32)(1-1/22)x = 1/12 + 1/52 + 1/72 + 1/112 + 1/132 + 1/172 + ...
We are now left with everything that is not even or a multiple of 3. The same type of process is continued over and over again, and we get:
...(1-1/p2)...(1-1/52)(1-1/32)(1-1/22)x = 1
which easily turns into
x = 1/[ (1-1/22)(1-1/32)(1-1/52)(1-1/72) ... (1-1/p2) ... ]
Now consider the odds that two positive integers do not share a common factor. There is a 1/4 chance that they are both even and therefore share the factor 2. So the odds that they are not both even (i.e. that one or the other is odd) are 3/4, which is (1-1/4). There is a 1/9 chance that they both are multiples of 3, or a (1-1/9) chance that one or the other is not a multiple of 3. So we have (1-1/4)(1-1/9). Then we factor in the (1-1/25) probability that one or the other is not a multiple of 5, and so on.
See also 0.0833333... and 1.202056....
This is the Somos quadratic recurrence constant, √(1√(2√(3√4...))) = (2/1)1/2 (3/2)1/4 (4/3)1/8 (5/4)1/16 ... and related to Sloane's sequence A52129. See also 576 and 1658880.
The reciprocal of the Lambert W function of e, which has the special property 1.76322283435191.7632228343519=e. Thus xx2 = (xx)x = x④3 = ex when x is this number. See 2.506184... for more.
The square root of π. This is the area under a bell curve of unit height and unit standard deviation. It is also equal to Gamma(1/2), and is sometimes also called (-1/2)!, the factorial of -1/2. See also 7.188082....
This is the 3rd hyper-root of 7, using the "higher" definition of the hyper4 operator: if x=1.855404429290030564371386293833..., then xxx = x④3 = x↑↑3 = 7.
See also 1.763222..., 1.855404..., 2.506184..., and 56.9612....
Many properties, mostly for trivial reasons (see 3.) See prime, powers of 2, doubling, Fibonacci.
The "gyromagnetic ratio of the electron", a dimensionless constant of physics notable for being known very precisely: within 12 significant figures or better. The "(53)" represents the magnitude of uncertainty in the last few digits: instead of ...153, those last 3 digits might be as low as 153-53=100, or as high as 153+53=206. This number is a favourite of amateur theorists in much the same way as the fine-structure constant.
The thickness in millimeters of MAD magazine number 26, used as the basis of the Potrzebie system of weights and measures by Donald Knuth and published in MAD #33 (June 1957).
2.3130367364335829063839516026417824763...
This is the number whose continued fraction expansion gives all the prime numbers: It is 2+1/(3+1/(5+1/(7+1/(11+1/(13+1/(17+1/(19+1/...))))))). The digits of this constant are Sloane's sequence A064442. Compare to 2.56654383217....
This is the so-called "Silver ratio", in analogy to the golden ratio, because it has similar properties. As a continued fraction it is 2+1/(2+1/(2+1/(...))), with 2's all the way; the golden ratio is the same but with 1's. It is the solution of the equation x2=2x+1, similar to the equation x2=x+1 for the golden ratio.
See also 1.32471... and 1.414213562373....
(the second Feigenbaum constant)
The second Feigenbaum constant, commonly designated by the Greek letter alpha. (The other Feigenbaum constant is 4.6692016091....)
2.50618414558876925629294092237784727177139605213321283014...
The solution of xx=10, and notable for being close to √2π.
It is appropriate to note here that this value is transcendental — and there is no "simple" (closed-form) way to turn xx=y into an expression for x in terms of y. Instead, the function is solved by Newton's method. For example, the value of x for xx=10 was calculated this way:
|
Despite the rather poor initial approximation X=2, it only takes 8 repetitions of steps 3 4 and 5 to get the first 14 digits correct and 10 repetitions to get 57 digits.
In general, xx=y can be solved for x in terms of y using the Lambert W function:
x = eW(ln(y)), or
x = ln(y)/W(ln(y)).
These are special cases of the more general solution to the inverse lower hyper4 function with the complete derivation given on my hyper4 page.
For instructions on how to calculate the Lambert W function, see the wikipedia page. Alternately, just go to Wolfram Alpha [230] and put in "x^x=10". I use Maxima; here are examples showing the calculation of 1.559610... and 1.763222...:
(%i1) exp(lambert_w(log(2.0))); (%o1) 1.559610469462369 (%i2) log(2.0)/lambert_w(log(2.0)); (%o2) 1.559610469462369 (%i3) % ^ %; (%o3) 2.0 (%i4) exp(lambert_w(log(float(%e)))); (%o4) 1.763222834351897 (%i5) 1.0/lambert_w(1.0); (%o5) 1.763222834351897 (%i6) % ^ %; (%o6) 2.718281828459046 (%i7) exp(lambert_w(log(10.0))); (%o7) 2.506184145588769 (%i8) log(10.0)/lambert_w(log(10.0)); (%o8) 2.506184145588769 (%i9) % ^ %; (%o9) 9.999999999999998Although xx=y cannot be solved precisely with "normal" functions like ln(x) and ex, there is an iterative solution for x1/x=y (see 1.444667...) that can be adapted to solve xx=y for certain values of y:
given: xx=y, y is known, find x.
1. Substitute x=1/z: (1/z)(1/z) = y
2. Substitute y=1/w: (1/z)(1/z) = 1/w
3. Take the reciprocal of both sides: z(1/z) = w
4. If w is not within the range (e-e,e(1/e))
— approximately (0.065988, 1.444667) — then
either there is no solution to xx=y or else the solution
cannot be found this way.
5. Otherwise, find the limit of the series w, ww,
www, ...: this is z (as shown by Euler).
6. Take the reciprocal to get x.
Example: starting with xx=10, we get w=1/10. Iterating, we get ww = 0.7943282347..., www = 0.1605727204..., wwww = 0.6909192287..., and so on, converging after about 350 iterations to 0.39901297826...; the reciprocal of 0.39901297826... is 2.50618414558... . (This solution, based on work of Euler, was pointed out to me by Fantini and Kloepfer.)
The equation xy=yx is much easier to solve, as is xy=xy.
Notable for being kinda close to the solution of xx=10.
(length of the inch in centimeters)
Since July 1 1959, by international agreement, the inch has been defined to be exactly 2.54 centimeters or 0.0254 meters. See 299792458 for the definition of the meter. See also 1609.344.
The reciprocal 1/2.54 is 0.3937007874015748031496...; see 39.37 and 99.9998.
2.5665438321713888444675291063322857517829728287023...
This is a real number that encodes the prime numbers in a way similar to the terms of a continued fraction. It is associated with Don Blazys, who claims to link it to the fine-structure constant, among other things.
If you know the sequence you want to encode, an approximation of a constant like this can be computed in this way:
100 ' Modified continued-fraction encoding for strictly-increasing 101 ' integer sequence. In this example we encode the prime numbers. 101 ' Terms are used in reverse order 989 ' add more terms here 990 bl = 29; 991 bl = ((1/bl)+1) * 23; 992 bl = ((1/bl)+1) * 19; 993 bl = ((1/bl)+1) * 17; 994 bl = ((1/bl)+1) * 13; 995 bl = ((1/bl)+1) * 11; 996 bl = ((1/bl)+1) * 7; 997 bl = ((1/bl)+1) * 5; 998 bl = ((1/bl)+1) * 3; 999 bl = ((1/bl)+1) * 2; 1000 ' We're done 1010 print bl; 1999 endUsing enough terms you can get a value with many digits of precision; the original terms of the sequence are obtained by reversing the calculation, like so:
integer part of 2.566543... is 2
1/((2.566543.../2)-1) = 3.530176...
integer part of 3.530176... is 3
1/((3.530176.../3)-1) = 5.658487...
integer part of 5.658487... is 5
1/((5.658487.../5)-1) = 7.593155...
(and so on...)
Each step of the calculation removes the integer part of the number, then takes the reciprocal to make a new value that has a nonzero integer part. By using a sufficiantly precise starting value, this iteration can "generate" arbitrarily many terms of the sequence used to generate the constant, in this case the prime numbers. If one had an infinitely precise starting value, one could generate all the primes. See also 2.313036....
As a general-purpose way to encode a sequence of integers, this method is less universal than the normal continued fractions method, because the encoding is one-to-one only when the sequence being encoded is a steadily-increasing sequence.
The square of Φ, the golden ratio. Among other things, it is the value of both sides of the equality:
Φ+1 = Φ2
2.66514414269022518865029724987313984827421131371465... = 2√2
This number is known as the Gelfond-Schneider constant. Along with eπ, it was shown to be transcendental by Gelfond's theorem (sometimes called the Gelfond-Schneider theorem). This theorem shows that if x is not 0 or 1 but is algebraic, and y is both algebraic and irrational, then xy is transcendental. It was proven independently by Gelfond and Schneider in 1934.
See also 1.632526919438..., 3.141592653..., 23.140692632779269005....
Khintchine's constant is the geometric mean of the terms of the continued fraction for most (but not all) real numbers. Rational numbers, roots of 3rd order polynomials and certain other classes of real numbers have patterns in their continued fraction expansion — so they do not obey this principle. However, the real numbers that do obey this average outnumber those that don't, and they outnumber by such a great extent, that if you picked a real number at "random" the probability that it would not have this average is 1/infinity.
(basis of natural logarithms)
e, base of natural logarithms, Euler's number, etc. Competes with the square root of 2 for second-most-famous non-integer after π. e is the limit of
(1 + 1/X)X
as X goes to infinity. An efficient way to calculate e goes like this:
e = 2
i = 2
f = 1
repeat until satisfied
f = f/i
e = e + f
i = i + 1
end repeat
which uses the well-known infinite series: e is the sum of the reciprocals of the factorials of all the natural numbers.
The solution of xx=27. :-)
There are so many properties of small numbers like this that it is somewhat tedious to list them all (but if you're interested look here). 3 is a prime, a triangular number, a Fibonacci number, the number of spatial dimensions of our universe, etc. etc.
There are many occurrences of a 3-times repetition in rituals, customs, stories, etc. Some examples include: the three knocks of Black Rod when calling the House of Commons to hear the address of the Sovereign at the opening of Parliament; three verses in the standard song format; the three pigs' houses (straw, wood, stone/brick) in the children's tale. The use of three (rather than two or four) is probably due to the fact that three is the minimum necessary to establish a pattern (such as a regular tempo) or to convey the impression of an ongoing sequence or succession.
3.14159264581... = 3 + 1/8 + 1/61 + 1/5020
The closest approximation to π using three terms of the greedy Egyptian fraction algorithm. It is somewhat more accurate than this one but requires a larger denominator term.
(π (pi), the best-known irrational constant)
The most well-known non-integral mathematical constant, the subject of several books, etc. Pi shows up in many places you don't expect it to (for instance, see 1.644934....)
There are lots of ways calculate π. One of the most efficient is Chudnovsky's series sum, which looks like this:
A = 545140134; B = 13591409; C = 640320;
D = C3; E = C/12; F = C/64; G = C2/96;
total = 0;
n = 0;
repeat until satisfied:
total = total + -1n
((6n)!(A n + B))/(n!3(3n)!Dn)
n = n + 1;
end repeat
π = E √C / total
π = 1 / (√F / G) total
The last two lines are equivalent, and come from the two different versions of the Chudnovsky calculation I have seen. Every time you repeat the loop adds more than 14 digits to the accuracy of the approximation.
Take a large integer N. Round up to the nearest multiple of N-1. Then round that number up to the nearest multiple of N-2. Continue until you get to the nearest multiple of 1, and call this final value F. For sufficiently large initial values of N, the ratio N2/F comes arbitrarily close to π. (This is from mathpages.com via MathWorld101; more esoteric formulas at the footnote.)
One of the famous problems from ancient times is called squaring the circle. The original problem was to use a straightedge and compass to determine the size of a square whose area is the same as that of a given circle. This is essentially equivalent to finding a precise formula for π that involves integers, the operations + - × /, and a few simple others like square root.
This problem eventually evolved into a more refined version, that of finding an integer polynomial to which π is a root. Numbers that can be expressed this way are algebraic, those that are not are transcendental. For various reasons it became important to be able to determine if certain numbers are algebraic or transcendental.
The transcendental nature of π was first shown by Lindemann in 1882. See also 1.632526919438... and 2.66514414269....
Digits of Pi
The following formula allows one to compute the Nth digit (in base 16) of π without computing all the preceding digits:
π = SUM [ (4/8n+1 - 2/8n+4 - 1/8n+5 - 1/8n+6) × 16-n ]
The following poem is a mnemonic for remembering the first 42 digits of π. The number of letters in each word corresponds to a digit, with 10-letter words for '0' digits. It was written in 1995 by Michael Keith based on "The Raven" by Edgar Allen Poe:
3.1 Poe, E. - 415 Near A Raven 926 Midnights so dreary, 535 tired and weary, 8979 Silently pondering volumes extolling 32384 all by-now obsolete lore. 62643 During my rather long nap 383 the weirdest tap! 27950 An ominous vibrating sound disturbing 288 my chamber's antedoor. 419716 "This", I whispered quietly, "I ignore".If you like this kind of thing, Mr Keith finished "The Raven" and went on to write several other modified versions of well-known bits of literature, then made an entire story around it, which he calls Cadaeic Cadenza. It has about 3800 words corresponding to the first 3834 digits of π. He later created the book Not A Wake which does the same thing in 10000 words, and many other interesting examples of constrained writing, all available at his website cadaeic.net.
3.14159267204... = (e (φ + 6))/5 - 1
One of many close approximations to π. This one achieves the closest possible approximation using 5 single digits or constants and 4 operations. Here are some others: with three constants: √4e-1 = 3.14215...; with four constants: ln((72 - e)/2) = 3.1415998...; with six constants (sort of): (4-φ√e)×(2/√7+1) = 3.141592653650... and √3+√2+1/(ln(7)-63) = 3.1415926535515... . (If this sort of thing amuses you, you might want to check out my inverse equation solver; the command line for this problem is: ries 3.1415926535897932 -Ox -x -NpSCL .)
3.1415269531... = 3 + 1/13 + 1/17 + 1/173
(an Egyptian value for π)
The numbers 13, 17 and 173 have been found together in ancient Egyptian records without explanation, but it is conjectured that they express an Egyptian fraction approximation to π. If so, it is a much better approximation than those attributed to Archimedes and Ptolemy.
The approximation to π given by the ratio 355 / 113. This approximation is admired mainly because it is "efficient": the fraction has 6 digits but the approximation gives you about 71/2 digits of π. It's also kind of easy to remember, if you remember the denominator first (because then you get "113, 355" which is a very simple pattern).
Along with 22/7, 355/113 is a member of the continued-fraction series for π. Continued fraction approximations can be used to get "optimal" rational approximations for any number. By "optimal" we mean the closest approximation that is possible with a given-size numerator and denominator. The continued fraction approximations for π are: 3/1, 22/7, 333/106, 355/113, 103993/33102, 104348/33215, 208341/66317, 312689/99532, 833719/265381, 1146408/364913, 4272943/1360120, 5419351/1725033, ...
To generate a continued-fraction series, you just keep truncating the fraction and taking the reciprocal:
3.141592653589... = 3 + 0.141592653589... = 3 + 1/7.062513305931...
7.062513305931... = 7 + 1/15.996594406685...
15.996594406685... = 15 + 1/1.003417231013...
1.003417231013... = 1 + 1/292.634591014395...
292.634591014395... = 292 + 1/1.575818089...
This gives you the terms of the continued fraction: 3, 7, 15, 1, 292, 1, 1, 1, 2, 1, 3, 1, 14, 2, ... (Sloane's A1203). You use these integers to make the actual continued fraction for π:
π = 3+1/(7+1/(15+1/(1+1/(292+1/...))))
The fact that 355/113 is an "efficient" approximation (as described above) is because the next term in the series (292) is relatively high. On average, continued-fraction series have much smaller terms most of the time (see Khintchine's constant). The beginning of the π series is an exception.
If you stop a continued fraction series at any point and reduce to a simple fraction, you get an approximation:
3+1/(7+1/(15+1/(1))) = 3+1/(7+1/(16)) = 3+1/(113/16) = 3+16/113 = 355/113
If you want to generate a whole series of numerators and denominators, use an algorithm like this:
(given: X = number to be converted) N = 1 D = 0 N1 = 0 D1 = 1 repeat until satisfied: let XI = integer part of X let X = fractional part of X let X = 1 / X let N2 = N1 let N1 = N let N = N1 * XI + N2 let D2 = D1 let D1 = D let D = D1 * XI + D2 print "New approximation: ", N, "/", D end repeatThe approximation 355/113 for π was known to the Chinese mathematician Zu Chongzhi around 480 AD.
(Ptolemaic value for π)
The approximation to pi used by Ptolemy.
3.141851... = 3 141/994 = (3 1/7 + 3 10/71) / 2
(Archimedes' value for π)
Some say that Archimedes used a value for pi that was "between 3 1/7 and 3 10/71", rather than simply 3 1/7; this would be an improvement since 3 10/71 is closer to the true value of pi. 3 141/994 is the average of the two approximations.
An approximation to pi given by the unitless expression:
(Planck energy times
the combined fuel economy of a Toyota Prius)
divided by
(the pressure in the centre of the earth times
the width of the English Channel at its narrowest point)
which is given in this xkcd cartoon. (All of the units cancel out, as you will see if you follow the links to each of these constants, and the approximation is correct to within the limits of measurement and/or experiment. I have given only 27 digits of precision, but more may be possible in the near future — watch this space! This formula is a great commentary on all the theories described at 137.035.)
22/7 (or 3+1/7), an approximation of π used in the time of Archimedes. The difference between 22/7 and π is given by the integral
∫0 to 1 [ x4 (1 - x)4 / (1 + x2) dx ]
3.160493827160... = 256/81 = 44/34 = 3+1/9+1/27+1/81
44/34 is an approximation to π used by the Egyptians, and it is also sort of close to √10, but it has a much more interesting property:
64/27 × 4/3 = 64/274/3 = 256/81.
There are an infinite number of pairs of rational numbers a and b such that ab=a.b. To show this, start with:
xy = x.y
then define L to be the log base x of y:
L = logxy
then the first equation becomes:
xxL = x xL
which (for x>1) reduces to:
xL = L+1
Solving for x, and substituting back for y, we get:
x = (L+1)(1/L)
y = xL = ((L+1)(1/L))L = L+1
This is the general solution for xy = x.y. (The same equations also happen to solve x④y=xy.)
To get both x and y to be rational numbers, define L to be 1/n for some integer n>1. Then you get:
x = (1/n+1)n = (n+1)n/nn = ((n+1)/n)n
y = (n+1)/n
x = yn
For n=1 you get x=y=2, which isn't a very interesting solution, but for n=2 you get this solution and for n=3 you get x=64/27 and y=4/3, with the product x.y=xy=256/81=3.160493827160...
As n gets larger, y approaches 1 and x approaches e because
e = lim (1 + 1/n)n
See also 1.632526919438... and the solution of xy=yx.
This has sometimes been used as an approximation to π.
Fans of the exponentiation function on integers may enjoy noticing such coincidences as 32 and 3125, both 5th powers, also being close to a 1-to-100 ratio. In the leading digits game embodied in OEIS sequence A88995, one looks for values of k such that 2k and 5k share several starting digits in common. As it turns out, all such pairs start with a 3, and all of the matching digits are leading digits of √10. See that page for more.
3.375 = 27/8 = (9/4)(3/2) = (9/4) × (3/2)
The values x=9/4 and y=3/2 give the simplest solution in rational fractions (non-integers) to the equations xy=xy and x④y=xy, where ④ is the lower-valued form of the hyper4 operator.
These equations can be solved easily. We will start with the x④y=xy equation. The lower hyper4 function x④y is equivalent to two exponents:
x④y = xxy-1
so we're really solving:
xxy-1 = xy
If x>1 we have:
xy-1 = y
and thus:
x = y1/(y-1)
(If you change y to l you can see the similarity to the solution of xy=yx. The same values of l and x that solve the xy=yx equation also solve x④l=xl.)
We can also express xy in terms of y:
xy = (y1/(y-1))y = yy/(y-1)
and now notice that this is equal to the product xy, because:
xy = yx = y.y1/(y-1) = y(y-1+1)/(y-1) = yy/(y-1)
Therefore, the solutions to x④y=xy also simultaneously solve xy=xy.
If 1/(y-1) is an integer then x and y will both be rational numbers; this happens when y is of the form (a+1)/a, where a is any nonzero integer. Then x is:
x = ((a+1)/a)a = (a+1)a/aa
The smallest non-trivial solution is when a=2, we get x=9/4 and y=3/2, and the value of x④y = xy = xy is 27/8=3.375.
This number is implicitly mentioned in the Bible in a few places; see 1260.
First page . . . Forward to page 3 . . . Last page (page 25)
Quick index: if you're looking for a specific number, start with whichever of these is closest: 0.065988... 1 1.618033... 3.141592... 4 12 16 21 24 29 39 46 52 64 68 89 107 137.03599... 158 231 256 365 616 714 1024 1729 4181 10080 45360 262144 1969920 73939133 4294967297 5×1011 1018 5.4×1027 1040 5.21...×1078 1.29...×10865 1040000 109152051 101036 101010100 — — footnotes Also, check out my large numbers and integer sequences pages.
 s.30
s.30