Notable Properties of Specific Numbers

First page . . . Back to page 2 . . . Forward to page 4 . . . Last page (page 25)

3.732050... = 2+√3 = tan(75^o)

This would be the number of years overall divided by the number of leap years in any set of 100 consecutive years, if only the "100" rule were used, as in: "Y is a leap year if Y/4 is an integer and Y/100 is not an integer". It is 100/24 because 24 out of the 100 years satisfy the criterion. See also 4.123711....

4.16989459467390571268...

This is the "circumference" or perimeter of an ellipse whose aspect ratio is the golden ratio, specifically with phi as its major axis and 1 as its minor axis. The circumference of an ellipse can be computed using the complete elliptic integral of the second kind, but various approximations exist to compute it in a more practical way. I used the Ivory-Bessel series sum described on the Wikipedia page, see Ellipse: Matric Properties: Circumference.

4.236067...

The cube of the golden ratio phi, and the value of these three expressions all involving Φ²:

Φ² × Φ = (Φ²}² - (Φ)² = (Φ²}³ / (Φ)³

Thus, Φ² and Φ are the answer to an old algebra problem (from ⁷⁸):

What two numbers are those whose product, difference of their squares, and the ratio or quotient of their cubes, are all equal to each other?

It is also equal to 1+2Φ. See also 2.618033...

4.6692016091...

The (first) Feigenbaum constant, commonly designated by the Greek letter delta.

It appears as the limit of the ratio of successive intervals between period-doubling domains in the iteration of a quadratic mapping, when varying the parameter continuously from the stable (single-attractor) domain towards the chaotic domain.

The phenomenon is illustrated and explained quite well by this Numberphile video : The Feigenbaum Constant (4.669), in which they look at the iteration

x <- l x (1-x)

where l is the parameter.

In the Mandelbrot set, it shows up as the ratio between each "circle" and the next smaller one in the series of "circles" on the real axis connected to the large cardioid. (Only the first of these, the one centred at -0.75, is actually a perfect circle.) For more information, click here.

The value is approximated to 7 digits by the formula π+arctan(e^π) (which is 4.6692019318...)

The second Feigenbaum constant is 2.5029078750....

Many properties, mostly for trivial reasons (see 3.) The third prime, a Fibonacci number, a pyramidal number, etc.

5.290316093...

This number is the highest solution to the equation e^x = Gamma(x+1), and corresponds to the point where the Gamma function starts to exceed the e^x function.

A perfect number. See 496 and my largenum notes for more.

Also a triangular number, a factorial, composite, etc.

Because 6 is in A1109 (see 204 for details about that) and because its square 36 is triangular, this makes 6 a triangular number whose square is also triangular, the only such case apart from 0 and 1.

6.283185... = 2π

2 π is seen often enough that it is sometimes treated as a constant in its own right, separate from π itself (see also π/2).

There has been a grass-roots movement (beginning roughly at the time of Palais' 2001 opinion article in The Mathematical Intelligencer [177]) to replace the use of π with this constant. Palais called it "tau", but used a new "three-legged pi" symbol 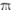instead of the Greek letter τ, and described a "blight of factors of 2" throughout mathematics and physics that might be eliminated by replacing π with .

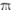Indeed, using this constant, some formulas become a little more elegant: we have cos(x+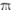)=cos(x) in place of the normal cos(x+2π)=cos(x); Euler's identity becomes ei=1 rather than e^π=-1 or e^π+1=0; and so on. However, "tau" is a fringe culture phenomenon, and not accepted for use in e.g. high school or university mathematics education.

6.5

According to Randall Munroe's What-If Numbers stream on Twitter, 6.5 is the "mass, in grams, of a kilometer-long strand of human hair". You'll find many similar numbers, most of them have units and/or are variable in value (example: "ounces of gold it would take to buy one ounce of 64GB MicroSD cards").

The smallest positive integer whose reciprocal has a pattern of more than one repeating digit: 1/7 = 0.142857142857... It is also the smallest number for which the digit sequence of 1/n is of length n-1 (the longest such a sequence can be). The next such numbers are 17, 19, 23, 29, 47, 59, 61, 97, 109, 113, ... (Sloane's integer sequence A6883). See 17 for more on this; see also my separate article, Fractions with Special Digit Sequences.

Tests for divisibility by 7 are difficult. About the best one I've found is as follows (demonstrated by testing 4156726):

Remove the last digit and subtract twice this digit from the remaining number: 415672 - 2×6 = 415660 (You are subtracting 21×d and dividing by 10, where d is that last digit.)
Repeat this process: 41566 - 0×2 = 41566, 4156 - 6×2 = 4144, 414 - 4×2 = 406, 40 - 6×2 = 28
The result is a multiple of 7 if and only if the original number is.

There is another divisibility test that works as follows:

Alternately add and subtract groups of 3 digits starting from the right: 726-156+004=574. (If the result is negative, drop the sign) (This is done because 7 is a factor of 1001.)
If greater than 999, repeat the previous step.
Add the 1's digit, 3 times the 10's digit and twice the 100's digit: 4+3×7+2×5=35. (The reason for the multipliers: 1 = 1 mod 7, 10 = 3 mod 7, and 100 = 2 mod 7)
If desired, repeat previous step until result is small enough to tell at a glance if it's a multiple of 7: 5+3×3=14.
The result is a multiple of 7 if and only if the original number is.

7 is considered "lucky" by many people and given much spiritual significance. The early religious and cultural use of the 7-day week almost certainly arose from the fact that the moon goes through its 4 phases in a bit over 28 days, which divides nicely into 7 days per phase. Another, different connection between moon phases and 7 is that there are 7 easily distinguishable, visible phases of the moon: waxing crescent, first-quarter, waxing gibbous, full, waning gibbous, third-quarter, waning crescent. The new moon doesn't count because you can never see it (the sun is too bright). And there is also the well-known count of the 7 moving objects in the sky: sun, moon, Mercury, Venus, Mars, Jupiter, Saturn.

7.188082728976 = π!

This is the Gamma function with an argument of π+1, equivalent to the factorial of π. See also 1.772453....

7.874007874... = √62

The square root of 62 has a remarkable digit pattern:

√62 = 7.874 007874 011811 019685 034448...

The "7874" repeats 6 digits later, then we get "11811" (which is 7874×3/2) and then "19685" (which is 7874×5/2).

A similar pattern with an amazing similarity is seen in the square root of 2:

√2 = 1.4 14 21 35 62 ...

Again we have "14" repeated twice, then 14×3/2 = 21, then 14×5/2 = 35.

These patterns of digits, and the recurrence of the ratios 2:2:3:5, is not a coincidence. They result from the fact that 62 times 127 squared equals 999998, which is a power of 10 minus 2; and similarly, 2 times 7 squared is 98. Note also that 62×127 = 7874, which are the first 4 digits of √62, and 2×7 = 14, the first 2 digits of √2.

For a full understanding, we start with

1/999998 = 0.000001000002000004000008000016000032000064...

a digit pattern featuring powers of 2 which is described in the 998 entry. Now it happens that 0.001000001 squared is 0.000001000002000001 (see 10201), and 0.001000001000001 squared is 0.000001000002000003...

Since 1/999998 = 0.000001000002000004... is a little bigger than this, it makes sense that its square root should be a little bigger than 0.000001000001000001:

√1/999998 = 0.001000001000001500002500004375007875...

The sequence (1, 2, 4, 8, 16, ...) has become (1, 1, 1.5, 2.5, 4.375, ...) Those two 1's make the repeated digits possible.

Now instead of the square root of 1/999998, we want the square root of an integer. Since the factors of 999998 are 2×31×127², we can multiply √1/999998 by 2×31×127, which is 7874. The 7874 goes inside the radical and becomes 7874², then most everything cancels out:

7874 √1/999998 = √7874×7874/999998 = √62×999998/999998 = √62

Therefore

√62 = 7874 √1/999998 = 7874 × 0.001000001000001500002500004375007875... = 7.874007874011811019685034448812007863...

So we started with 999998, which is 2 fewer than a power of 10, and is divisible by 127². The remaining part of 999998 is 62, and we found that the square root of 62 has the digits "7874", which is 62×127, and these digits are repeated.

We saw a sequence (1, 1, 1.5, 2.5, 4.375, ...). These numbers come from the Taylor series expansion of √1/(1-2x), which is:

√1/(1-2x) = 1 + x + 3x²/2 + 5x³/2 + 35x⁴/8 + 63x⁵/8 + ...

√1/(1-2x) is related to √1/999998 in a simple way: if x=10^-6, then √1/(1-2x) = √1/(1-0.000002) = √1/0.999998. This has the same digits as √1/999998, but with the decimal point shifted 3 places over.

Because √999998 is close to √1000000 = 1000, the fraction 1000/127 is very close to √62. This is similar to the coincidence 10/7 ≈ √2, and see 1/127.

The coefficients of the Taylor series (the infinite polynomial) are the central binomial coefficients (OEIS sequence A000984) divided by the powers of 2: (1/1, 2/2, 6/4, 20/8, 70/16, 252/32, 924/64, 3432/128, 12870/256, 48620/512, ...). After reducing to simplest form, the numerators are OEIS sequence A001790 (1, 1, 3, 5, 35, 63, 231, 429, 6435, 12155, ...), and the denominators are OEIS sequence A060818, the highest powers of 2 that divide the factorial of N (1, 1, 2, 2, 8, 8, 16, 16, 128, 128, 256, ...).

Square Root Digits in Other Bases

This all generalises to other number bases, not just base 10. Whenever a multiple of a square plus 2 equals an exact power of the base, there is an integer whose square root has a block of repeating digits when displayed in that base. Here are some of the more remarkable examples in other bases:

In base 2:
   √28 = 101.0100 1010100 11111111 ...
   √1820 = 101010.1010100 1010101010100 1111111111111 1010101010100 1110101010100 ...
   √116508 = 101010101.0101010100 1010101010101010100 1111111111111111111 1010101010101010100 1110101010101010100 1011111111111111111 0001111111111111110 ...
   √167772 = 110011001.100110011000 110011001100110011001 001100110011001100101 111111111111111111111 011111111111111111111 010011001100110011000 ...
   √85598 = 100100100.1001001001000 1001001001001001001000 1101101101101101101101 0110110110110110110110 0111111111111111111111 0111111111111111111111 0011111111111111111110 ...
In base 3:
   √3 = 1.2 012 021 222 ...
In base 4:
   √1820 = 222.2221111110333333311111032222211333330133331033331...
   √116508 = 11111.11110222222222133333333322222222213111111102333333332033333332...
In base 5:
   √1735 = 131.31 13131 22222 13131 21211 44444 .....
In base 6:
   √276 = 24.34 02434 04053 ...
In base 7:
   √977423 = 2611.43464 0261143464 0421565362 ...
In base 8:
   √85598 = 444.444422222221555555533333331777777677777771777777...
In base 16:
   √167772 = 199.998CCCCC999997FFFFEFFFFF4CCCC...

Here are some base 23 examples, in which almost every pair of digits adds up to 'M' (which is the highest digit in base 23):

In base 23:
√16448427 = 7F7.F7 7F7F7 BBBBB 7F7F7 ACACA 5H5H5 ...
√2434958270224475 = 7F7F7F.7F7F7 7F7F7F7F7F7 BBBBBBBBBBB 7F7F7F7F7F7 ACACACACACA 5G5G5G5G5G5 74747474746 BBBBBBBBBBA ...

For a lot more about this sort of thing, see my separate article Fractions with Special Digit Sequences; see also 89, 998, 9801, 9899, and 997002999.

The smallest "non-trivial" cube: 8=2³=2×2×2.

When specifying directions on a map, most people choose from one of these 8 directions: north, northeast, east, southeast, south, southwest, west, and northwest. These are the 8 directions a queen or king in chess can move. The knight moves in 8 directions too, but not the same 8.

In three-dimensional space there are 8 "diagonal" ways to move, corresponding to the eight "octants" you get if you divide the three-dimensional space with three mutually-perpendicular planes.

In 4-dimensional space-time, there are 8 non-diagonal directions: up, down, left, right, forward, back, future, and past.

Apart from the trivial cases of 0 and 1, 8 is the smallest number for which the sum of the digits of its cube is equal to the number: 8³ = 512, 5 + 1 + 2 = 8. The largest number with this property is 27, and it is perhaps of interest that 8 and 27 are themselves cubes.

As mentioned in the 17 entry, 8 and 9 are the only pair of consecutive integers that are nontrivial integer powers of integers. See also 25.

8.794143

A modern value of the "solar parallax", in arc-minutes. This is the angle subtended by the radius of the Earth at the mean distance from the Earth to the Sun. Measuring this angle was the purpose of the Venus transit observations in the 17^th through 19^th centuries used to establish the length of the astronomical unit and thus the scale of the solar system. See 149597870691 for more.

9 is the largest single-digit number. It would also be the least frequently used digit if it were not for the tendency of businesses to set prices that end with one or more 9's. In situations where the number doesn't matter much (like street or apartment numbers) it is the least frequently used.

Casting Out Nines

Because 9 is one less than the base of our number system, it is easy to see if a number is divisible by 9 by adding the digits (and repeating on the result if necessary). This process is sometimes called casting out nines. Similar processes can be developed for divisibility by 99, 999, etc. or any number that divides one of these numbers; see 11, 37 and 101 for examples.

When you were learning your multiplication tables you might have noticed that if you were dividing a 2-digit number by 9, you could check to see if the two digits add up to 9, and if they do the answer is the first digit plus 1, or 10 minus the last digit: 63 / 9 = 6 + 1 or 10 - 3. This idea can be extended to give an easy way to divide a three-digit number by 9:

1. To start with, you need to know that the number is divisible by 9: The digits must add up to 9, 18 or 27. If they don't, subtract enough from the 3-digit number so that the digits add up to 9 or 18 (the amount you subtract is the remainder that will be left over after dividing by 9.)

2. Easy case: if it ends in 0, take the first two digits divided by 9, and add a 0 to the end. For example, 540 / 9 = 60, because 54 / 9 = 6 and you add a 0. You're done.

3. Otherwise, take the first digit, followed by the last digit subtracted from 10. For example, 477 / 9 gives 43: a 4, followed by a 3 which is 10 - 7. (This obviously only works if the 3-digit number is a multiple of 9 to start with, which is why you had to subtract the remainder in step 1.)

4. If the result from step 3 is less than or equal to the first two digits of the original number, add 10 to get the answer. Since 43 is smaller than 47 (the first two digits of 477) we need to add 10 to get 53.

Another example: 819 / 9: Step 3 gives 81, but 81 is equal to the first two digits of 819 so we add 10 to get the answer, 91.

This division technique is part of my method for testing divisibility by 27.

9.869604...

π squared. In certain ancient cultures it was believed (or assumed for convenience) that π was the square root of 10.

(ten, the most common base)

10 is both a triangular and tetrahedral number. 10 is also composite, semiprime, etc.

Number of fingers on a typical human. 10 has many other cultural properties resulting from that, or indirectly through other cultural properties (the use of 10 as our base is a cultural phenomenon).

The number of dimensions in a superstring theory that unifies general relativity with the other benefits of string theories. 11-D superstring theory dates back to Cremmer, Julia and Scherk in 1978.

There are three ways to test for divisibility by 11.

The first, and more commonly known, is to alternately add and subtract digits starting from the right. For example, to test the number 1234 you would compute 4-3+2-1. The original number is a multiple of 11 if and only if the answer is a (positive, negative or zero) multiple of 11 (in this case we get 2, so the answer is no).

Another method is to add digits in groups of two starting (again) from the right, and repeat the process if necessary, until you get 2 identical digits (multiple of 11) or something else (not a multiple of 11). To test 51381 this way, we'd add 5+13+81 to get 99, which is two identical digits, so 51381 is a multiple of 11.

However, the third method is the most useful, because it also gives the value of the quotient. It works by repeatedly subtracting the last digit from the remaining digits: 5138-1=5137, 513-7=506, 50-6=44, 4-4=0. If this process results in 0, the original number was divisible by 11, and the sequence of last-digits gives the quotient: The last digits were 1, 7, 6 and 4 so 51381/11=4671.

The word "eleven" does not fit into the pattern of the numbers 13 to 19; the original word in Old English probably meant "one left over".

Ours go to 11!

The main reason why so many things are grouped in 12's (inches, months, donuts, hours) is because 12 can be divided evenly in more different ways than any other number of its size: It's divisible in 4 non-trivial ways (2, 3, 4 and 6). The next record-setter is 24 (hours in a day; case of beer), which is divisible in 6 different ways. Other popular division numbers like 60 (minutes, seconds) and 360 (angular degrees) are also factorisation record-setters.

Highly Composite Numbers

Numbers that set records for number of divisors are sometimes called "highly composite" numbers (Sloane's A2182). Here are the record-setters, arranged in a way that helps illustrate a couple points mentioned later:

	1
	&nbs









	2









	4






	6

cellpadding="0" cellspacing="5"> p; 10080 1081080 110880 12 120 1260 1441440 15120 166320 1680 180 20160 2162160 221760 24 240 2520 25200 27720 277200 2882880 332640 36 360 3603600 4324320 45360 48 498960 5040 50400 55440 554400 60 6486480 665280 720 720720 7207200 7560 83160 840 8648640

Some interesting things to note:

The sequence sometimes jumps a lot (like from 2520 to 5040) and sometimes a little (like from 50400 to 55440). This behaviour continues, but the gaps get generally smaller; the last time it jumps by a factor of 2 appears to be the jump from 2520 to 5040.
If a number is a record-setter, that number times 10 is also sometimes a record-setter, but not the number times 100.
All the factorials up to 7!=5040 are record-setters, but 8!=40320 and all higher factorials are not.
The record-setters gradually incorporate bigger and bigger prime factors, but sometimes a prime factor is added, goes away, and then comes back. For example, the first multiple of 11 in the sequence is 27720; the next two (45360 and 50400) are not multiples of 11; after that 11 comes back to stay. Most higher prime factors come and go multiple times.
The record-setters with repeating digits, starting with 720720, continue for about 20 terms. The digit-pattern results from the factors of 1001.
Although not shown in the table, the number of divisors of a record-setter is often also a record-setter — for example, 6 has 4 divisors; 12 has 6 divisors; 60 has 12 divisors; 360 has 24 divisors. (See also 840, 5040, 293318625600 and 195643523275200.)

For more about highly-composite numbers, see 840, 45360, 720720, 3603600, 245044800, 278914005382139703576000, 2054221614063184107682218077003539824552559296000 and 457936×10⁹¹⁷.

A long-standing and fairly famous problem in mathematics (the "kissing number problem") involved proving that one cannot arrange more than 12 spheres of equal size so as to touch a central sphere. It seems pretty obvious if you try it, but there is also a fair amount of space between the spheres and one could perhaps in theory work out some sort of asymmetrical arrangement that would allow a 13^th sphere to be added. It was eventually proven that 12 really is the limit.

Related to the kissing problem is the sphere packing problem, which is determining how to fit the greatest number of equal-sized spheres into a given space. The familiar arrangement (seen in fruit stands for example) has each sphere touching 12 others; this was also proven to be the best possible. The fruit-stand arrangement is called a "face-centred cubic lattice packing". The typical stack of fruit in a fruit stand (usually a tetrahedron or a square pyramid) does not suggest the notion of "face-centred cubic", however they are actually equivalent (in the case of the tetrahedron stack, by rotating the entire lattice). To describe this with coordinates: spheres of radius √2/2 can be placed at every point (x,y,z) such that each of the three coordinates is an integer and the sum x+y+z is even; in such an arrangement each sphere touches 12 others. (For example, the sphere centred at the origin (0,0,0) touches four centred at (0,±1,±1), another four at (±1,0,±1) and four more at (±1,±1,0)).

A cuboctahedron is a solid with 12 vertices and 14 sides (six squares and eight triangles). This shape, along with octahedra, can be used to completely fill space in all directions; each cuboctahedron touches six other cuboctahedra. If you ignore the octahedra, the cuboctahedra line up in a cube-like grid arrangement. When this is done with cuboctahedra of just the right size, the space-filling arrangement places the centres of the cuboctahedra at every position (x,y,z) such that all three coordinates are even integers, and places the vertices at every position (x,y,z) such that one coordinate is even and the other two odd; these are exactly the same coordinates as the just-described face-centred cubic lattice sphere packing.

The word "twelve" does not fit into the pattern of the number-names 13 "thirteen" to 19 "nineteen"; the original word in Old English probably meant "two left over".

The word dozen comes (through French) from Latin duodecem ("two-ten")⁴⁴ and thus is more similar to thirteen than most people realise.

To test a number (example 746245952673) for divisibility by 13:

Remove the last digit, then add 4 times that digit to the remaining number: 74624595267+4×3 = 74624595279. (Each time you are adding 39d=(40-1)d and dividing by 10, where d is that removed digit.)
Repeat until it gets down to 40 or less: 7462459527+4×9 = 7462459563; 746245956+4×3 = 746245968; 74624596+4×8=74624628; 7462462+4×8 = 7462494; 746249+4×4 = 746265; 74626+4×5 = 74646; 7464+4×6 = 7488; 748+4×8 = 780; 78+4×0 = 78; 7+4×8 = 39.
If this process results in 0, 13, 26 or 39 the original number is a multiple of 13; otherwise it isn't.

Another method goes like this:

Alternately add and subtract groups of 3 digits starting from the right: 673-952+245-746=-780. (If the result is negative, drop the sign.) (This works because 13 is a factor of 1001.)
If greater than 999, repeat the previous step.
Add 4 times the 100's digit plus 3 times the 10's digit, and subtract the 1's digit: 4×7+3×8-0=52. (The reason for the multipliers: 1 = 1 mod 13, 10 = -3 mod 13, and 100 = -4 mod 13; the signs are all reversed to make the result be usually positive.)
If necessary, repeat the previous step until the result is less than 40, or small enough to tell at a glance if it's a multiple of 13: 3×5-2=13.
The result is a multiple of 13 if and only if the original number is.

For information about superstitions related to this number, see triskaidekaphobia.

A square pyramidal number, and also composite.

A Rhombic dodecahedron is a three dimensional figure with 14 vertices positioned like the 8 vertices of a cube combined with the 6 vertices of an octahedron that is suitably scaled (so that all 12 of its rhomboid faces are planar). Rhombic dodecahedra can be used to completely fill space in all directions; each shares a face with 12 neighbors. The centres of the rhombic dodecahedra then coincide with the centres of spheres placed in a close packing in a symmetric, regular repeating lattice pattern with each sphere touching 12 others, a "face-centred cubic" lattice. The 4-dimensional analogue of the rhombic dodecahedron is the 24-cell.

The Unistable Polyhedron problem

Any convex polyhedron has at least one face that it can rest on without falling over (proof: if it didn't, it would be a perpetual-motion machine!). Most have more than one stable face. Finding a polyhedron with a minimum of faces and only one face on which it can rest was posed in 1966 by J. H. Conway, M. Goldberg and R. K. Guy as their "problem 66-12(b)":

It is obvious that a regular homogeneous tetrahedron will rest in stable position on top of a horizontal table when lying on any one of its faces. [...] (b) Give an example of a homogeneous convex polyhedron which will rest in a stable position when lying on only one of its faces.

The implied requirements are that the polyhedron has flat faces, is rigid and solid (not hollow), and of uniform density. Guy found a 19-face solution in 1968. As far as is known as of 2014, the minimum number of faces is 14, see [231]. Conveniently, the year of Reshetov's publication ends in 14.

14 is the lowest base with 'easy' divisibility tests for 5 different primes, assuming that the casting out 11's method is considered 'easy'.

In base 10 there are fairly easy tests for divisibility by the prime numbers 2, 3, 5 and 11. The lowest base with easy tests for four primes is base 6 (2, 3, 5 and 7). In base 14, you can test for divisibility by 2, 3, 5, 7 and 13.

The record-setters for this property (bases with high numbers of testable primes) are shown here. The primes in bold are tested just by looking at the last digit; the primes in the plain font are tested by the digit-addition technique (casting out 9's); the primes in italic are tested by alternate addition and subtraction (see the entry on 11 for a description):

base	N	prime divisors
2	2	2, 3
4	3	2, 3, 5
6	4	2, 3, 5, 7
14	5	2, 3, 5, 7, 13
34	6	2, 3, 5, 7, 11, 17
154	7	2, 3, 5, 7, 11, 17, 31
286	8	2, 3, 5, 7, 11, 13, 19, 41
714	9	2, 3, 5, 7, 11, 13, 17, 23, 31
5796	10	2, 3, 5, 7, 11, 17, 19, 23, 31, 61
18446	11	2, 3, 5, 7, 11, 13, 17, 23, 31, 43, 401
90364	12	2, 3, 5, 7, 11, 13, 19, 29, 31, 41, 53, 331
304590	13	2, 3, 5, 7, 11, 13, 17, 19, 23, 41, 53, 71, 821
1013726	14	2, 3, 5, 7, 11, 13, 17, 19, 23, 37, 41, 43, 103, 139
5617821	15	2, 3, 5, 7, 11, 13, 17, 29, 31, 37, 41, 43, 101, 107, 137
23738714	16	2, 3, 5, 7, 11, 13, 17, 19, 23, 31, 41, 47, 97, 127, 157, 173
123702370	17	2, 3, 5, 7, 11, 13, 17, 19, 29, 31, 41, 53, 73, 83, 137, 151, 797
556876530	18	2, 3, 5, 7, 11, 17, 19, 23, 29, 31, 37, 43, 67, 79, 101, 109, 167, 241
3760113566	19	2, 3, 5, 7, 11, 13, 17, 19, 31, 37, 41, 53, 61, 67, 71, 73, 131, 853, 929

Notice that all of these except 5617821 are even.

If you want the record-setters for all divisors (not just prime divisors), check the entry for 29. If you don't think the casting out 11's method should count, see the entry for 66.

First page . . . Back to page 2 . . . Forward to page 4 . . . Last page (page 25)

Quick index: if you're looking for a specific number, start with whichever of these is closest: 0.065988... 1 1.618033... 3.141592... 4 12 16 21 24 29 39 46 52 64 68 89 107 137.03599... 158 231 256 365 616 714 1024 1729 4181 10080 45360 262144 1969920 73939133 4294967297 5×10¹¹ 10¹⁸ 5.4×10²⁷ 10⁴⁰ 5.21...×10⁷⁸ 1.29...×10⁸⁶⁵ 10⁴⁰⁰⁰⁰ 10^9152051 10^10³⁶ 10^{10^10¹⁰⁰} — — footnotes Also, check out my large numbers and integer sequences pages.

s.30