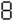Notable Properties of Specific Numbers

First page . . . Back to page 9 . . . Forward to page 11 . . . Last page (page 25)

144 is 12², and also happens to be the 12^th Fibonacci number by the standard definition. See also 61917364224.

One of the largest numbers, that is not a power of 10, that has a specific word (gross) assigned to it. Moser is another.

Gratuitous connection to 27: 144 = (3+3+3+3)×(3+3+3+3); rearrange the parentheses to get 3+3+3+(3×3)+3+3+3 = 27.

145

145 = 1!+4!+5!; see 40585.

145 is the largest member of a loop in the Happy number iteration starting with 4: 4² = 16; 1²+6² = 37; 3²+7² = 58; 5²+8² = 89; 8²+9² = 145; 1²+4²+5² = 42; 4²+2² = 20; 2²+0² = 4; repeat.

All "non-happy" numbers ultimately end up in this loop. For example, starting with 8 we get: 8² = 64; 6²+4² = 52; 5²+2² = 29; 2²+9² = 85; 8²+5² = 89 and proceed as above.

There is a Numberphile video on this, 145 and the Melancoil.

149

149 is prime, and is also prime when reversed (941). Such numbers are called Emirps. A palindrome prime such as 101 does not count.

150

(a 5-smooth number)

150 = 2×3×5². It has no prime factors larger than 5, and this makes it a 5-smooth number. 5-smooth numbers are sometimes called "regular numbers" or Hamming numbers; they are the numbers whose reciprocal has a terminating digit expansion in base 60. They include the 3-smooth numbers plus: 5, 10, 15, 20, 25, 30, 40, 45, 50, 60, 75, 80, 90, 100, 120, 125, 135, 150, 160, 180, 200, 225, 240, 250, 270, 300, 320, 360, 375, 400, 405, 450, 480, 500, 540, 600, 625, 640, 675, 720, 750, 800, 810, 900, 960, ... That list is Sloane's A80193 and is generated by multiplying all the 3-smooth numbers by 5, 25, and other higher powers of 5. The complete list of 5-smooth numbers is Sloane's A51037.

153

153 = 5!+4!+3!+2!+1!.

153 = 1³+5³+3³. It is the smallest number that is the sum of powers of its own digits, where the power is the same as the number of digits, aside from the trivial 1-digit cases like 8=8¹. These are called Armstrong or "narcissistic" numbers. The next few numbers with this property are: 370, 371, 407, 1634, 4150, 4151, 8208, 9474, 54748, ... (OEIS sequence A23052). See also 8208, 4679307774, and 115132219018763992565095597973971522401.

153 = 17+16+15+...+3+2+1, the 17^th triangular number.

153 is the magic constant of this 4×4 magic square drawn with calculator-style seven-segment display digits, that has the curious property of being able to be turned upside down and retain its magic properties:

When inverted the magic constant becomes 177.

Compare this to the similar square shown at 176; a lot of similar 4×4 magic squares can be made by substituting out certain digits wherever they occur in either the 10's place or the 1's place.

There is also a similar 3×3 invertible square, see 45.

153 is also 100+28+25, and appears in a New Testament story as a number of fish. A lot has been made of this in connection with the Enneagram, a system of personality type classification.

Gratuitous connections to 27: 15³/(1×5³) = 27; or 15³/(1×5×3) = 225 and 22+5 = 27.

158

(the fibonomial triangle)

158 is the sum of row 7 of the "fibonomial triangle". This is a triangle of numbers similar to Pascal's triangle, using Fibonacci factorials in place of normal factorials. The numbers in the triangle are called fibonomials:

1 sum: 1 1 1 sum: 2 1 1 1 sum: 3 1 2 2 1 sum: 6 1 3 6 3 1 sum: 14 1 5 15 15 5 1 sum: 42 1 8 40 60 40 8 1 sum: 158 1 13 104 260 260 104 13 1 sum: 756 1 21 273 1092 1820 1092 273 21 1 sum: 4594 1 34 714 4641 12376 12376 4641 714 34 1 sum: 35532

These numbers are defined similarly to the binomial coefficients in Pascal's triangle but using the Fibonacci numbers F₁=1, F₂=1, F₃=2, F₄=3, etc. (more here). For example, the 4^th element in the 8^th row (260) is F₇F₆F₅/F₃F₂F₁ = 13×8×5/2×1×1. The general form is F_n...F_n-k+1/F_k...F₁. It is not immediately obvious that this formula always gives an integer. It does — because of the property of fibonacci numbers that if A is divisible by B, F_A is divisible by F_B, combined with the fact that the ordinary binomial coefficients use the formula {n}...(n-k+1)/k...1, which itself is always an integer for somewhat simpler reasons.

On Pascal's triangle, the second number on each row is the sequence of integers; here they are the Fibonacci numbers. On Pascal's triangle the following number is an oblong number; here the 3^rd items (1, 2, 6, 15, 40, 104, 273, ...) are golden rectangle numbers. The next numbers after that (1, 3, 15, 60, 260, 1092, ...) are F_n×F_n+1×F_n+2/2.⁶⁸,⁶⁹

The same transformation can be done again to create the meta-fibonomial triangle.

160

The length limit of a text message in the "short messaging service" (SMS), a committee-driven standard adopted by mobile phone companies in the 1990s. This size comes from the 140-byte payload size limit of packets in the SS7 MAP protocol, combined with the use of 7-bit character encoding (specifically, the 7-bit variant of GSM 03.38), which gives 160 characters because 140×8/7 = 160.

163

163 appears in the "Ramanujan constant" e^pi×√163, which is very nearly an integer. It is the largest Heegner number, a set of 9 integers that share this same property. See e^π, and 262537412640768743.999999... for a description of this and some related amazing numbers.

The appearance of √163 in the Ramanujan constant is related to √-163 and the Monster group, due to the Monstrous moonshine phenomena.

√-163 can also be used to demonstrate that x²-x+41 yields prime numbers for all x from 1 to 40.⁹⁵

163 = 1 + 2 × 3 ⁴ can be produced on most "algebraic" calculators by keying 1 + 2 × 3 x^y 4 =. If you have an RPN calculator you would key in either 1 2 3 4 x^y × + or 4 3 2 1 + × x^y (depending on how the x^y key works). See also 10^{1.0979×10¹⁹}.

Gratuitous connection to 27: 163₁₀ = 61₂₇ and 61₁₀ = 27₂₇ — or another way of saying the same thing: 2×27+7 = 61, and 6×27+1 = 163

168

168 is the order of the group PSL(2,7), which describes the symmetries of the "Fano plane" and the automorphisms of the "Klein quartic". These are two important abstract geometric objects.

The Klein quartic is the solution to the equation x³y+y³+x=0 with x,y complex, and its surface is like a 3-holed torus (as opposed to a normal torus with just one hole). It is a two-dimensional surface that can be covered with a finite number of heptagons, joined 3 at each vertex — like a warped Dodecahedron made from heptagons. It takes 24 heptagons to do this[194], and you end up with 84 edges and 56 vertices. No other surface can be covered with a smaller number of heptagons in a regular way. It has 168 automorphisms because you can "rotate" the tiling around the centre of any of the heptagons, and there are 24 heptagons to choose from: 7×24=168. (On a dodecahedron or most of the other "normal" Platonic solids, when you rotate one face, one other face stays put and rotates the other way. Paradoxically, when you rotate one of the heptagons in the Klein quartic, two others stay put, with one rotating twice as far and the other rotating four times as far (or three times as far in the opposite direction)!)

The Fano plane is a set of seven lines and seven points (another illustration is on John Baez' page [176]) with the property that any two lines uniquely determine a point and any two points uniquely determine a line. It is useful (among other things) as a way to show the symmetry of the basis elements of the Octonions and how their multiplication rules work⁴⁵. Imagine that the 7 points have been labeled 1 through 7 and the 7 lines have been labeled A through G. When this is done, there are 21 unique letter-number combinations like A1, A2, A4, B1, B3, etc. have been chosen out of the complete set of 49. The Fano plane's 168-fold symmetry is evident in how many ways you can relabel the points and lines such that the same 21 out of 49 letter-number groups occur. It is easy to see that line A has to still have points 1, 2 and 4 on it; but you can pick any of the 7 lines to be line A. With a little work you can see that if you stick to this choice of which line is labeled A, you can pick from all 4×3×2×1=4! combinations of where to place the labels 3, 5, 6 and 7. Thus there are 7×24 equivalent labelings.

Of course, 168=24×7 is also the number of hours in a week. See 10080.

169

169 is a "powerful" number, meaning that all of its prime factors occur at least twice. It's pretty easy to see that all squares are powerful, in this case we have 13². Similarly 144 = 12² = 2⁴×3². More generally, anything expressible as X²Y³, where X and Y are positive integers and X+Y is greater than 2, is a powerful number. The powerful numbers, Sloane's A1694, include many highly composite numbers.

173.297929 ≈ 29.530588853 × 223 / 38

(eclipse season interval in days)

The number of mean solar days between each time the nodes of the Moon's orbit align with the sun. This is the length of time between each eclipse season (the time of year when lunar and/or solar eclipses occur). The oldest known calendars of the Sumerians of Mesopotamia were based on the synodic month and the eclipse season (which was called by the same name that later became used for the solar year). Near the equator, the tropical year does not matter too much, but the moon was very important inasmuch as it provides light at night and eclipses were considered a very important event. The eclipse season is a little less than half a year, because the tilt of the moon's orbit keeps shifting; after 18 years it comes around to the same time of year again.

176

The magic constant of a 4×4 magic square drawn with calculator-style seven-segment display digits, that has the curious property of being able to be turned upside down and/or viewed in a mirror, retaining its magic properties:

Numberphile did a video, "Special Magic Square", with Prof. Roger Bowley showing the square and all its properties.

You may notice that all digits are 1, 2, 5, or 8; these digits occur in the 10's place once in each row and once in each column; and likewise for the 1's place; that all of these digits are the same when turned upside-down; and when viewed in a mirror the 2 and 5 turn into each other while the 1 and 8 remain the same.

Compare this to the similar square at 153; a lot of similar 4×4 magic squares can be made by substituting out certain digits wherever they occur in either the 10's place or the 1's place.

177

The magic constant of a 3×3 magic square that contains all prime numbers:

17 89 71 113 59 5 47 29 101

When the primes in this square are listed in order (5, 17, 29, 47, 59, 71, 89, 101, 113) a simple pattern can be seen: The successive differences are 12, 12, 18, 12, 12, 18, 12, 12. The values 12 and 18 are simple multiples of the primorial 2×3=6, and the symmetry of their arrangement is also important.

See also 177.

199 is also a Woodall number: 2×10²-1. See also 383.

The reciprocal 1/199 exhibits a pattern similar to that of 1/998. Here are the digits, broken into groups to show the structure; the repeating pattern is 99 digits long:

1/199 = 0.005 025 125 628140703517587939698492462311557788944 7236180904522613065326633165829145728 64 32 16 08 04 02 01 005 025 125 6281407...

Since 1/199 = 5/995, we have the digits of 1/995 (which contain powers of 5, for the reason explained under 998) multiplied by 5, which just means that the 0^th power of 5 does not appear. The powers of 2 also appear, in the opposite order at the end, for reasons originating in the fact that 2×5=10 and we are working with base 10 digits. For more on this, see my separate article Fractions with Special Digit Sequences; see also 89, 99.9998, 9801, 9899, and 997002999

204

204 = 17*12, the product of the numerator and denominator of 17/12, which is an approximation to the square root of 2 formed by the Pell numbers and another similar sequence. The first few numbers like this are: 1, 6, 35, 204, 1189, 6930, 40391, 235416, 1372105, 7997214, ... (Sloane's integer sequence A1109). The sequence follows the pattern:

A_n = 6 A_n-1 - A_n-2

(for example, 204=6×35-6 and 1189=6×204-35).

square triangular numbers

A really nifty property of these numbers is that their squares are also triangular: 1, 36, 1225, 41616, 1413721, 48024900, 1631432881, ... (OEIS sequence A1110). Note that 6 is in A1109 and is also triangular.

206.7682827(47)

Approximate mass ratio between an electron an a muon, using CODATA 2022 recommended values⁵⁰ (the "(78)" is an indication of uncertainty). The muon is about 207 times heavier, as a result when it binds with a nucleus its charge distribution is about 207 smaller. This means that a muon bound with a proton forms an atom that is chemically similar to hydrogen but with 207 times smaller diameter. See also 137.03599....

210

(7 primorial)

210 is a primorial: the product of the first N primes: 210=2×3×5×7. The primorials are: 2, 6, 30, 210, 2310, 30030, 510510, 9699690, 223092870, 6469693230, 200560490130, 7420738134810, 304250263527210, ... (Sloane's A2110).

210 is a 3-d oblong number, the product 5×6×7. Curiously, it is also 1×2×3 + 2×3×4 + 3×4×5 + 4×5×6 (see 3024 for more).

Since it is also 14×15, it is another example of a number that is the product of consecutive integers in two different ways (see also 120, 720, 5040).

For a while, 2 is the most common gap between consecutive prime numbers. Then (starting at about 100, and permanently after 1000), gaps of 6 occur most often. Up at around 10³⁵, it shifts to 30. There is a conjecture that above about 10⁴²⁵ the most common prime gap is 210.

Base 210 is also a record-setter for tests for divisibility by primes. See 66.

213

A member of the (Lionel) Levine sequence, Sloane's A11784, which is generated by the following constuction:

Create an infinite sequence of finite sequences, each determined by the previous one
Each sequence starts with "1"
Each successive member of each sequence is the same or increases by 1
Start with (1, 1) as the initial sequence
For the next sequence, use the previous sequence to tell how many times to repeat each integer, starting from the end (this is the opposite of A14644 described in the entry for 272)
The infinite sequence A11784 is the last number in each finite sequence so generated (or, equivalently, "1" followed by the number of terms in each finite sequence; or, equivalently, "1, 2" followed by the sum of the terms in each finite sequence).

The list of sequences you get is:

1 1
1 2
1 1 2
1 1 2 3
1 1 1 2 2 3 4
1 1 1 1 2 2 2 3 3 4 4 5 6 7
1 1 1 1 1 1 1 2 2 2 2 2 2 3 3 3 3 3 4 4 4 4 5 5 5 5 6 6 6 7 7 7 8 8 9 9 10 10 11 12 13 14
...

For example, the row after "1 1 2 3" has three 1's, followed by two 2's, followed by one 3, followed by one 4.

The sequence so generated grows rather quickly: The number of digits in the n^th term is roughly Φⁿ/42. Numberphile have a nice video about it.

216

216 is a cube, 6³, and is the sum of three consecutive cubes⁷²: 3³ + 4³ + 5³ = 6³. See also 25, 143, 8000 and 31858749840007945920321.

8 pieces are required to construct a puzzle that can be assembled as a 6×6×6 cube and reassembled into the three smaller cubes. The 6 "slices" of the puzzle would appear as follows, with letters a through h representing the eight puzzle pieces:

f f f f f h f f f f f h f f b b b b f f f f f e f f f f f e f f b b b b f f f f f e f f f f f e f f f b b b g g g e e e g g g e e e g g g b b b g g g e e e g g g e e e g g g e e e g g g e e e g g g e e e g g g e e e slice-1 slice-2 slice-3 f f b b b b a a b b b b a a b b b b f f b b b b a a b b b b a a b b b b c c b b b b c c b b b b c c b b b b c c b b b b c c b b b b c c b b b b c c c e e e c c c e e e c c c d d d c c c e e e c c c e e e c c c d d d slice-4 slice-5 slice-6

216 is the magic constant for this "multiplicative" magic square:

2	9	12
36	6	1
3	4	18

which is built on the principle of doing an elementwise multiplication (Hadamard product) on the following two components:

2	1	4		1	9	3
4	2	1	o	9	3	1
1	4	2		3	1	9

both of which satisfy the row, column, and diagonal requirements but with repeated numbers. See also 1514, 6720 and 6227020800.

216 = 8×27 = 2³×3³, and had spiritual significance in ancient times because it was the product of the "first two" cubes (they didn't count 1³ as a cube).

It is also 6×6×6, and is the value of Φ(666), the number of integers less than and relatively prime to 666.

In the 1998 movie π (a.k.a. "Pi the Movie"), the Qabbalistic Jews are searching for a sequence of 216 Hebrew letters, or a 216-digit number (which is the same thing in ancient Hebrew, since the letters of the Hebrew alphabet are used to represent the digits of numbers). See also 187 and 304805.

220

220 and 284 form an amicable pair, an idea that goes back to the time of Pythagoras. If you add the factors of 220 you get 284 and vice versa. The search for amicable numbers is closely related to the classical question of finding perfect numbers.

See also 276.

225

The image of 20 under the "Climb to a Prime" mapping, part of a long-standing conjecture of J.H. Conway that was disproven in 2017. The conjecture involves taking the prime factorisation of a number, and forming a new number from all the digits of the prime factors and their exponents, in order: 20 = 2²×5 → 225. The process contiunues: 225 = 3²×5² → 3252; 3252 = 2²×3×271 → 223271; 223271 = 29×7699 → 297699; and so on. If one reaches a prime number (as with 60 and 35149) then the process stops; but if one were to iterate forever and/or enter a repeating loop, then Conway's conjecture would be false. The latter turned out to be the case; see 13532385396179.

231

231 appears as a denominator in the "greedy" Egyptian fraction for 3/7: ³/₇ = ¹/₃ + ¹/₁₁ + ¹/₂₃₁.

Egyptian Fractions

To the best of our knowledge, the ancient Egyptians had no general notation for an arbitrary fraction A/B. They had a special symbol for ²/₃, and any other fractions were expressed as a sum of "unit fractions", fractions of unity, such as ¹/₃ and ¹/₇. For example, instead of ³/₄ they wrote ¹/₂+¹/₄, and instead of ⁵/₆ they wrote ¹/₂+¹/₃. By convention, they always expressed it as a sum of different unit fractions (for example, ²/₇ could not be written ¹/₇+¹/₇, but ¹/₄+¹/₂₈ or ¹/₅+¹/₂₀+¹/₂₈ were OK), and the fractions were always listed largest-first (that is, smallest denominators first).

It is not entirely known why they did it this way. It could have been for practical reasons in performing physical divisions. For example, imagine dividing 2 equal bushels of grain among 7 people. Each person should get ²/₇ of a bushel. The simple approach would be to divide each into 7 equal parts (give each person ¹/₇ plus ¹/₇). But a fair division into 7 parts is difficult; 4 is much easier (use a balance, or the "I split, you choose" method, to divide in half; then repeat). So, divide each bushel into 4 equal parts, and give ¹/₄ bushel to each person; the remaining ¹/₄ bushel then is divided into 7, which is much easier than the original task. ²/₇ = ¹/₄ + ¹/₂₈.

It is possible to express any fraction as a sum of unit fractions, and usually in more than one different way. There are several different algorithms for converting a fraction like ³/₇ into an Egyptian fraction sum. One, called the "greedy" algorithm, works by subtracting the largest possible unit fraction each time and repeating:

Given: Fraction X/Y, where X and Y are positive integers and X 1: Let A be the smallest integer such that AX ≥ Y
2: 1/A is the first (or next) term in the Egyptian fraction.
3: Compute X/Y - 1/A and reduce to lowest terms. The result is the new X/Y. If nonzero, go back to step 1 and repeat.

This algorithm always produces an answer with a finite number of terms, but the denominators sometimes get really large. Starting with ³/₇ we get:

³/₇ = ¹/₃ + ²/₂₁
²/₂₁ = ¹/₁₁ + ¹/₂₃₁
therefore ³/₇ = ¹/₃ + ¹/₁₁ + ¹/₂₃₁

233 is a Fibonacci number and is also prime. The prime Fibonacci numbers are: F₃=2, F₄=3, F₅=5, F₇=13, F₁₁=89, F₁₃=233, F₁₇=1597, F₂₃=28657, F₂₉=514229, F₄₃=433494437, ... (Sloane's A5478). You may notice that (except for F₄=3), each prime Fibonacci number has a prime index. This is related to a more general property of Fibonacci numbers (see ²⁰ and [141]):

for N≥3, F_M is divisible by F_N if (and only if) M is divisible by N

239

This prime number appears in one of the earliest known geometrically converging formulas for computing π:

π/4 = 4 arctan(1/5) - arctan(1/239) = SUM [ (-2ⁿ)/(2n+1)(5²ⁿ⁺¹) - (-1ⁿ)/(2n+1)(239²ⁿ⁺¹) ]

This formula works because of this special relationship between 5 and 239 through their squares:

2 × 13⁴ = 239² + 1 = 57122

and

2 × 13 = 5² + 1 = 26

and

arctan(x) + arctan(y) = arctan( (x + y) / (1 - x y) )

This relationship makes it possible to show that a geometric construction of 4 right triangles in the proportion 1 :: 1/5 :: (√26)/5 and one triangle in the proportion 1 :: 1/239 :: (√57122)/239 can be used to produce a triangle in the proportion 1 :: 1 :: √2. Also related to this is the fact that 239/169 = 239/13² is a good close approximation to the square root of 2.

You might wonder, why do all that when you could compute π/4 directly from the arctangent of 1:

π/4 = arctan(1) = SUM [ (-1ⁿ)/(2n+1) ] = 1 - 1/3 + 1/5 - 1/7 + 1/9 - ...

The reason is that this series converges too slowly to be of any use. The 5²ⁿ⁺¹ in the denominator in the series above makes it converge quickly enough so that you get about 1.398 = log₁₀(5²) digits of π for each term you evaluate.

239 is the smallest factor of 9999999 that is not also a factor of some smaller string of 9's, and therefore 239 is the smallest number whose reciprocal has a 7-digit repeating pattern: 1/239=0.00418410041841004184... See also 27 and 757.

Here are two rather obscure properties of 239:

239 is the largest number that cannot be expressed as the sum of 8 (or fewer) cubes (it requires 9: 239 = 5³ + 3³ + 3³ + 3³ + 2³ + 2³ + 2³ + 2³ + 1³). The only other such number is 23. 239 also requires the maximum number of terms to be expressed as a sum of squares (4 squares, 239 = 15² + 3² + 2² + 1²) or of 4th powers (19 4th powers). It does not require the maximum number of 5th powers.

Define the "sum of prime factors" sopf(N) to be the sum of each of the prime factors of N, counting a prime more than once if N is a multiple of its square, cube, etc. So, for example, sopf(42) = 2 + 3 + 7 = 12, and sopf(27) = 3 + 3 + 3 = 9. sopf(N) = N only if N is prime, or if N is 1 or 4. Now consider the sum N + sopf(N). As N increases, this value increases irregularly. Some values never occur — for example, there is no N such that N + sopf(N) equals 12 — and other values occur more often — for example, there are two 14's and two 23's. The value 239 occurs often enough that if you add the sopf(N)'s for all N's that have N+sopf(N)=239, you get a sum greater than 239. 239 is the first number for which this occurs (the next few are 1439, 2159, 4319).

(Personal: 239 is another street number where I have lived. The famous HAKMEM⁷² file was MIT AI memo number 239.)

240

(a Fibonacci factorial)

240 is a "Fibonacci factorial", the product of the first 6 Fibonacci numbers: 1×1×2×3×5×8 = 240. See also 158.

It is known that in 8-dimensional space, the greatest number of spheres of equal size that can touch a single central sphere is 240. The arrangement that produces this is called the E₈ lattice, a repeating arrangement of points in 8-dimensional space that has the symmetries of the E8 group, a mathematical object that has applications in theoretical physics. See also 24 and 196560.

243

243 = 3⁵ = 9×27, and has a few cool properties. It is a perfect totient number, along with all other powers of 3. There is more about these numbers on a separate page here.

If we divide 5³ by 3⁵, we get a 27-digit repeating decimal with the digits 514403292181069958847736625. These 27 digits taken as an integer have the 370 property: the average of all possible permutations of its digits is equal to itself.

First page . . . Back to page 9 . . . Forward to page 11 . . . Last page (page 25)

Quick index: if you're looking for a specific number, start with whichever of these is closest: 0.065988... 1 1.618033... 3.141592... 4 12 16 21 24 29 39 46 52 64 68 89 107 137.03599... 158 231 256 365 616 714 1024 1729 4181 10080 45360 262144 1969920 73939133 4294967297 5×10¹¹ 10¹⁸ 5.4×10²⁷ 10⁴⁰ 5.21...×10⁷⁸ 1.29...×10⁸⁶⁵ 10⁴⁰⁰⁰⁰ 10^9152051 10^10³⁶ 10^{10^10¹⁰⁰} — — footnotes Also, check out my large numbers and integer sequences pages.

s.30