Second-Order Embedded Julia Set
Robert P. Munafo, 2012 Apr 21.
Truly the most stunning features of the Mandelbrot Set, when viewed with the aid of the Distance-Estimator function, are the higher-order Embedded Julia Sets.
Here is an example (click on it to enlarge):
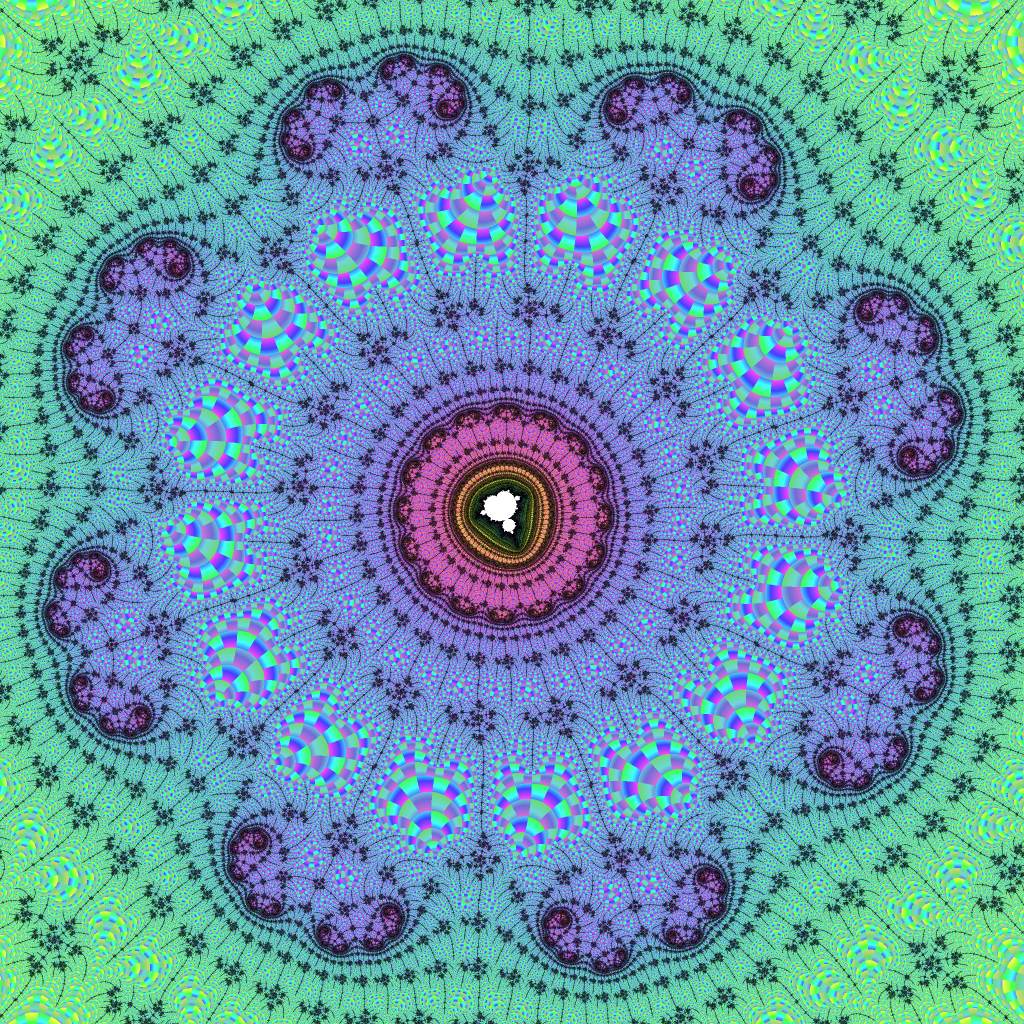
A second-order embedded Julia set
Just as Embedded Julia Sets are found by exploring very close to an island Mu-molecule, the second-order Embedded Julia Sets are found by exploring very close to an island — namely, the island at the center of a first-order embedded Julia set, or an island at the center of a paramecium.
In the term "second-order embedded Julia set", the order indicates how many islands you have gone close to while zooming in. An island counts only if it is not part of the mu-unit of a larger island which has already been counted. Every new mu-unit you get close to introduces a new "distortion field" (more accurately, tuning) that creates Julia Sets, and the place you explore in relation to this mu-unit determines the shape of the Julia set for that order. Each time you go to a higher order, another Julia Set shape is added to the nested symmetric filaments around the island at the center.
Zoom Sequence
During the course of this sequence we encounter tuning and non-tuning Embedded Julia Sets. The atom domain views (the right image in each pair) show which of the embedded Julia sets represent a new tuning period.
 | 
|
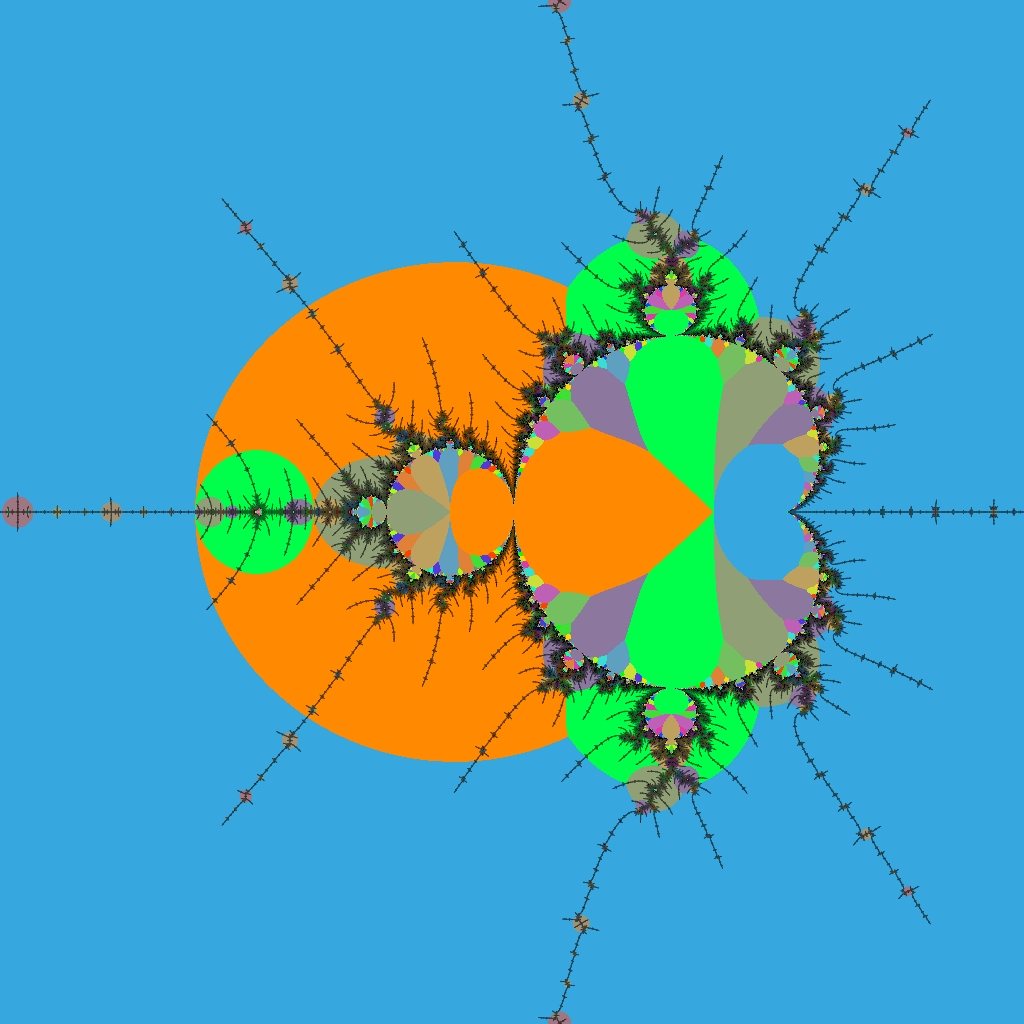
This is the period-3 island R2F(1/2B1)S. On the left is an ordinary view combining dwell, binary decomposition and distance estimator information showing the filaments.
On the right we see atom domains (or period domains). Period-3 (the period of R2F(1/2B1)S) is pink; period 6 is bright green; period 9 is cyan, and so on.
 | 
|
Here we see some filaments within the "Seahorse valley" area of R2F(1/2B1)S. The R2-name of this cusp is R2F(1/2B1)S.C(1/2)-.
In the period-domains image we see some higher periods near the left side, but most of the image is dominated by the bright green of the period-6 mu-atom R2F(1/2B1)S.1/2a.
 | 
|
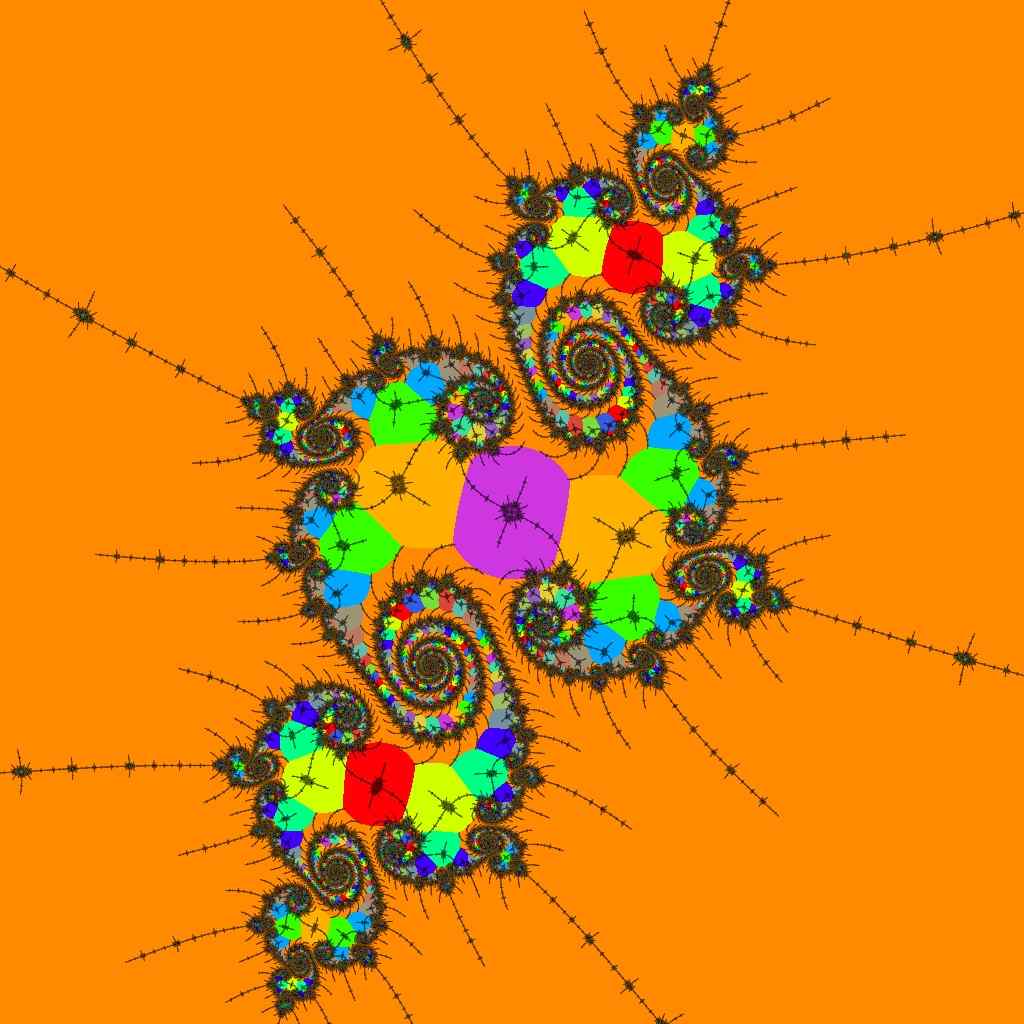
This is a first-order, 2-fold embedded Julia set within R2F(1/2B1)S.C(1/2)-.
In the normal DEM-dwell hybrid view on the left, contrasting color highlights show where the dwell values increase significantly at the boundary of the embedded Julia set.
Many new colors are seen in the period domain image on the right, showing the locations and periods of the embedded Julia set's nucleus and paramecia. As we continue to zoom in, this image will be mainly yellow, the color corresponding to the period-101 mu-molecule at the center of the 2-fold embedded Julia set.
 | 
|
This is the 4-fold nucleus of the embedded Julia set. The dwell values change significantly (seen by the distinct difference in color between the inside and outside of the nucleus), but the right image is dominated by the solid yellow of the period 101 domain.
 | 
|
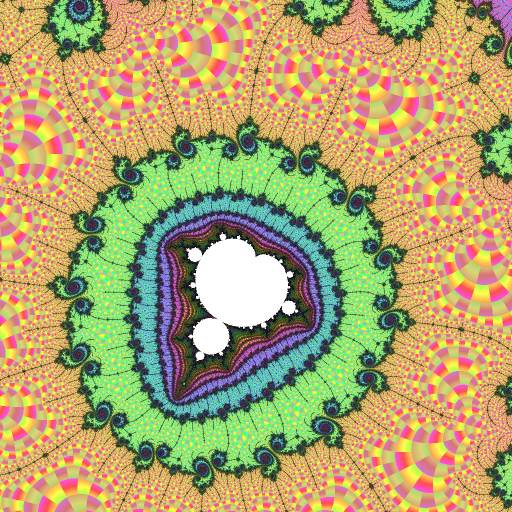Now we see the period-101 island. As with R2F(1/2B1)S, this island "tunes" the area around it, creating a nested concentric series of rings of features, doubling in number at each stage.
There are also new period domains in the right-hand image; these periods are all multiples of 101: salmon for period 202, purple for period 303, etc.
 | 
|
Here we approach the elephant valley or .C(0) cusp region of the period-101 island.
 | 
|
In these views there is plenty going on in the filaments, but little color contrast in the dwell values on the left. On the right, everything is yellow because the strongest tuning is still that of the period-101 island (which is completely surrounding us, though it is now out of sight).
 | 
|
This 2-fold embedded Julia set, is an "echo" of the original 2-fold embedded Julia set (seen above at size 4.5×10-6). The dwell values do not change significantly (resulting in lack of contrasting colors in the left image), and there are no new period domains in the right image.
 | 
|
A 4-fold "echo" of the original embedded Julia set. Again there is no significant contrast and the dominant period is 101.
 | 
|
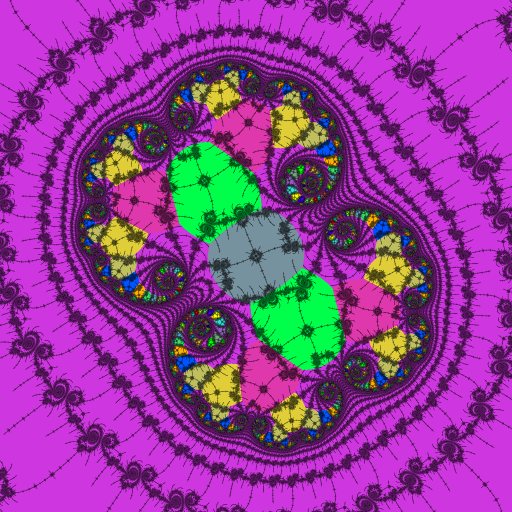
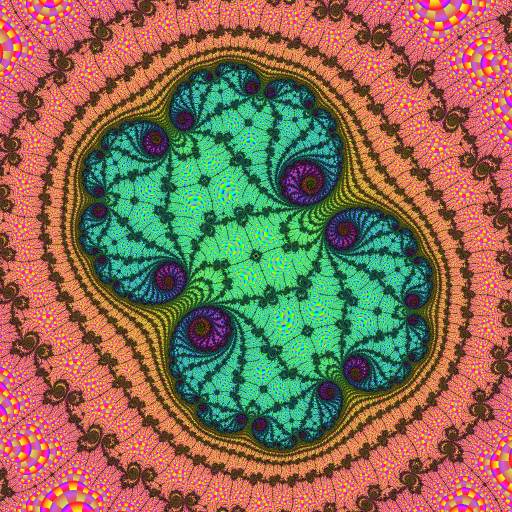Now we arrive at the second-order embedded Julia set. Significant color contrast makes it stand out in the dwell view on the left.
Unlike the "echo" embedded Julia sets above, this time there are lots of new period domains. These show the locations and periods of the nucleus and paramecia. As we proceed further the dominant period will be 2123, the period of the influencing island of this second-order embedded Julia set. This period shows up as blue in the right-hand image.
 | 
|
Another 4-fold "echo" of the original embedded Julia set. Here there is no contrast in either view. The period-domain image is the solid blue of period 2123.
 | 
|
This is the 4-fold symmetric nucleus of the second-order embedded Julia set. This time the dwell values jump significantly (seen by the contrasting colors in the left image) but there is no strong local tuning (evident from the solid blue of the right image).
 | 
|
Now we arrive at the period-2123 island at the center of the second-order embedded Julia set.
Here each of the concentric binary rings that approach the island as their limit has its own set of binary rings.
In the right image, period domains of its child mu-atoms can be seen: the period-4246 .1/2a (red), period-6369 .1/3a (yellow), etc.
See also second-order satellite, 2-fold embedded Julia set, n-fold embedded Julia set.
revisions: 20020418 oldest on record; 20120421 add zoom sequence
From the Mandelbrot Set Glossary and Encyclopedia, by Robert Munafo, (c) 1987-2023. Mu-ency index
This page was written in the "embarrassingly readable" markup language RHTF, and was last updated on 2022 Feb 22.
s.27