Lavaurs Algorithm

Robert P. Munafo, 2023 Jun 15.

The Lavaurs algorithm is a method for finding the locations of all mu-atoms in relation to each other, ordered by increasing external argument (which increase as one goes counter-clockwise around the Mandelbrot set).

The algorithm is most often described in terms of fractions n/d where the denominator d is a number of the form 2^p-1 for some period p. As described in the external argument article these fractions occur in pairs, with both fractions in a pair leading to the cusp of a mu-atom of period p. The continent seed is special, being the only mu-atom of period 1. Its denominator is 2¹-1 = 1, and there are two fractions 0/1 and 1/1 that are treated as being equivalent.

The Lavaurs algorithm was described in English for the first time by Prof. Bodil Branner in a talk to the AMS Chaos and Fractals conference in Providence, RI, USA in August 1988. That description is:

Lavaurs algorithm. We represent a t ∈ ]0,1[ as the point e^2πit on the unit circle S¹. If two rationals with odd denominator are equivalent, then we connect the two corresponding points in S¹ by an arc of a circle in D perpendicular to the boundary S¹. Recursively, using the period k of the rationals, we can construct the equivalence classes as follows:
   1. Connect 1/3 and 2/3.
   2. Suppose all points corresponding to rationals of period l for 2 ≤ l < k have been connected. Then points corresponding to rationals of period k are connected pairwise following the two rules:
   (i) all arcs are disjoint,
   (ii) if t₁ is the smallest rational in ]0,1[ of period k which has not yet been connected, then connect t₁ to the smallest possible t₂ > t₁ observing rule (i).
   The proof of the algorithm is a detailed analysis of the order of periodic points in Julia sets and the order of hyperbolic components in the Mandelbrot set.

I met with Prof. Branner later the same day and learned about the algorithm. It is simplified by the (non-obvious) fact that any "rational with odd denominator" can be expressed as a fraction with a denominator 2^p-1 (using Euler's theorem). These are not the "two rationals [that] are equivalent"; that phrase instead refers to the two rationals whose external rays lead to the same cusp of a mu-atom (see the "External Angles of Cusps" section in the external argument article).

For a fraction with denominator 2^p-1 (provided that the fraction does not reduce to something with a smaller denominator 2^f-1), the number p is the period found by iterating the process of doubling modulo 1, that is, starting with x equal to the fraction and repeatedly transforming x to a new value x' by the function:

x → 2x if x<1/2
2x-1 otherwise

until a cycle is found, with p being the number of steps in the cycle¹.

Because all fractions with odd denominator are equivalent to fractions with denominator 2^p-1, and because the algorithm as stated instructs one to start with period 2 and proceed to period 3, then 4, then 5 and so on, denominators other than 2^p-1 can be ignored. In addition, the fractions 1/3 and 2/3 do not need to have their own step in the instructions, as they fit into the general procedure (those fractions have period 2 under the doubling function, and 3=2²-1). Lastly, there is no particular reason to place the fractions on "a circle S¹"; a simple line stretching from 0 to 1 will do, and makes it easier to work out on paper.

Here I translate Lavaurs into a more direct and obvious description:

Start with the fractions 0/1 and 1/1. Mark these at endpoints of a line which can be interpreted as going from 0 to 1, or from 0.00000... to 0.11111.... if expressed as external argument binary expansions. All external arguments fall somewhere in between. This line represents the first "pair", the fractions 0/1 and 1/1.

Follow the rest of the steps in order of increasing period p, starting with p=2, then p=3, then p=4, and so on.

For each period p, add points on the line that correspond to all fractions with denominator 2^p-1, and numerators from 1 through 2^p-2; but do not add any fraxtions if they are equal to a fraction that was added previously (for example, 5/15 is the same as 1/3, so we'll add 1/3 when working on period 2, but we'll skip 5/15 when we get to period 4).

Match up the new fractions by connecting them in pairs, with each pair being joined by a curved line or "arc" that lies entirely above the line segment between the two fractions being joined.
     - Do not connect to any fractions that already have arcs connecting them.
     - Do this starting from the lowest of the new fractions and proceeding towards the highest. After forming each pair, continue with the lowest remaining unpaired fraction.
     - Do not allow arcs to cross, but always choose the lowest available pair that can be reached without crossing. For example 6/15 cannot be connected to 7/15 because that would require crossing the existing arc from 3/7 to 4/7. Instead 6/15 must be paired with 9/15.

Illustration

Here the "arcs" will be drawn in ASCII graphics.

We start with a line going from 0 to 1:

0.....................................................1 - - 0 1

Start with period 2. The denominator is 2²-1=3. Add the fractions 1/3 and 2/3 to the line:

0.................1.................2.................1 - - - - 0 3 3 1

Pair up the two fractions by connecting them with an arc:

,-----------. / \ / \ / \ 0.................1.................2.................1 - - - - 0 3 3 1

Proceed to period 3, and denominator 2³-1=7. Add the fractions with denominator 7 to the line:

,-----------. / \ / \ / \ 0.......1.......2.1....3.......4....2.5.......6.......1 - - - - - - - - - - 0 7 7 3 7 7 3 7 7 1

Pair up each of these fractions in the obvious way:

,-----------. / \ ,-----. / ,-----. \ .-----. / \ / / \ \ / \ 0.......1.......2.1....3.......4....2.5.......6.......1 - - - - - - - - - - 0 7 7 3 7 7 3 7 7 1

Proceed to period 4, and denominator 2⁴-1=15. Add the fractions with denominator 15 to the line, except for 5/15 which is the same as 1/3 and 10/15 which is the same as 2/3:

,-----------. / \ ,-----. / ,-----. \ .-----. / \ / / \ \ / \ 0 .1..2.1..3..4.2.1..6.3..7..8.4..9.2.5.11.12.6.13.14.1 - - - - - - - - -- - -- -- - -- - - -- -- - -- -- - 0 15 15 7 15 15 7 3 15 7 15 15 7 15 3 7 15 15 7 15 15 1

The first two pairs are easy:

,-----------. / \ ,-----. / ,-----. \ .-----. ,--. / ,--. \ / / \ \ / \ 0 .1..2.1..3..4.2.1..6.3..7..8.4..9.2.5.11.12.6.13.14.1 - - - - - - - - -- - -- -- - -- - - -- -- - -- -- - 0 15 15 7 15 15 7 3 15 7 15 15 7 15 3 7 15 15 7 15 15 1

The next fraction 6/15 must be matched up with something. We can't draw an arc from it to 7/15 (or to 8/15) because the existing arc from 3/7 to 4/7 is in the way. So instead, we connect 6/15 with 9/15:

,-----------. / ,-------. \ ,-----. / / ,-----. \ \ .-----. ,--. / ,--. \ / / / \ \ \ / \ 0 .1..2.1..3..4.2.1..6.3..7..8.4..9.2.5.11.12.6.13.14.1 - - - - - - - - -- - -- -- - -- - - -- -- - -- -- - 0 15 15 7 15 15 7 3 15 7 15 15 7 15 3 7 15 15 7 15 15 1

Match up the remaining fractions: 7/15 with 8/15, 11/15 with 12/15, and 13/15 with 14/15. The result is:

,-----------. / ,-------. \ ,-----. / / ,-----. \ \ .-----. ,--. / ,--. \ / / / ,--. \ \ \ / ,-. \ ,-. 0 .1..2.1..3..4.2.1..6.3..7..8.4..9.2.5.11.12.6.13.14.1 - - - - - - - - -- - -- -- - -- - - -- -- - -- -- - 0 15 15 7 15 15 7 3 15 7 15 15 7 15 3 7 15 15 7 15 15 1

Here is the same information "sideways", with a 6-digit decimal expansion for each fraction.

0.000000 0/1 0.066667 1/15. 0.133333 2/15' 0.142857 1/7---. 0.200000 3/15. | 0.266667 4/15' | 0.285714 2/7---' 0.333333 1/3-------. 0.400000 6/15----. | 0.428571 3/7---. | | 0.466667 7/15. | | | 0.533333 8/15' | | | 0.571429 4/7---' | | 0.600000 9/15----' | 0.666667 2/3-------' 0.714286 5/7---. 0.733333 11/15. | 0.800000 12/15' | 0.857143 6/7---' 0.866667 13/15. 0.933333 14/15' 0.999999 1/1

Circle Representation

Although the line layouts illustrated above are simplest to draw, it is more common to see the fractions arranged around a circle with the arcs internal to it.

Starting with the horizontal line layout, this is done by bending the right end of the line up so that 1/1 is at the "3-o-clock" position on a circle, leaving 11/15 at the bottom "6-o-clock" position, and bringing the rest of the line around so that 7/15 and 8/15 are at the "9-o-clock" position, 4/15 is at the top, and 0/1 meets up with 1/1 to complete the circle. The result is the left figure here:

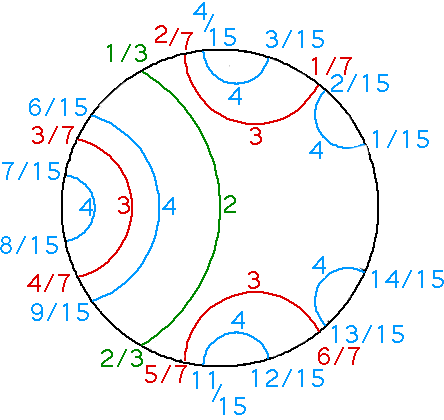
Lavaurs arcs for periods 2, 3, and 4

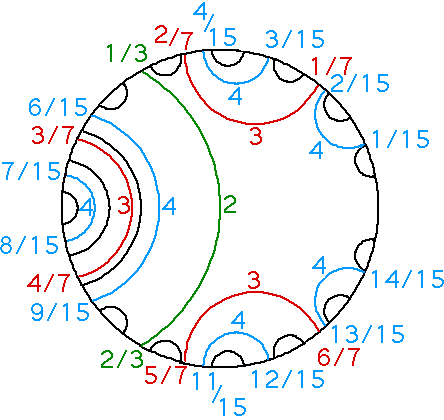
Lavaurs diagram with period-5 arcs in black

both are modified from the original by Michael Frame

The right figure shows the result after adding arcs for the fractions with 31 in the denominator.

Topological Equivalence to the Mandelbrot Set

Notice that the circle has been divided into segments by the arcs. Two segments are "neighbors" if they share one of the arcs as a boundary.

Each arc corresponds to two external rays that meet at a cusp of a mu-atom. Because the rays meet each other, the two points they lead to are the same point.

This suggests that we could "shrink" all the arcs down to zero length, by bringing the endpoints of each arc together, and adjusting everything else as necessary so that neighboring segments still touch each other (but now touching at only one point). Branner states this as follows:

The Abstract Mandelbrot Set. From the equivalence relation on rationals we can get a model of an abstract Mandelbrot set on a pinched disc: each connecting arc is pinched to a point. One can prove that the abstract Mandelbrot set is homeomorphic to M if and only if M is locally connected.²

The regions into which the circle has been divided correspond to mu-atoms. For example, the largest region that is bounded partly by one green 2 arc, two red 3 arcs and two blue 4 arcs is the continent seed, and the region that lies between a blue 4 arc and the green 2 arc is the period 2 mu-atom R2.1/2a.

If this is done with all of the arcs (an infinite number of arcs!) and if the all-important MLC conjecture is true², the result would be topologically equivalent to the Mandelbrot set in all of its infinite detail. Points on the circle itself correspond to the filament structure.

Enumeration of Features

The Lavaurs algorithm gives a way to identify all of the mu-atoms, and a way to count how many there are of each period; furthermore it lets us locate them in relation to each other. This is similar to the results of the algorithms presented in the enumeration of features article; however those algorithms only give total statistics, such as the number of islands and non-island mu-atoms of period 5 (11 and 4 respectively).

See also the Farey addition article, which shows how to get the ordering of a set of child mu-atoms that share a parent.

footnotes

1 : The doubling function is relevant because of the way that the Julia set's squaring iteration z → z²+c affects the two sets of p external rays, corresponding to the iterated x values as their angles. There are two sets, one for each of the external arguments that meet each other at the cusp of a mu-atom. The rays with these 2p different external angles can be traced in the plane of the Julia set whose parameter c is the location of that mu-atom cusp. In the Julia plane for parameter c, the 2p rays lead in pairs to p different points. The pairs of rays form boundaries that partition the complex plane into nonintersecting regions that each contain one of the p points in the limit cycle for c.

2 : The question of Mandelbrot set local connectivity is still an open conjecture, called "MLC". Much work has been done over more than 35 years, and pieces of the conjecture (e.g. at points that satisfy certain restricted definitions) have been proven.

Mu-ency main page — index — recent changes — DEMZ

This page was written in the "embarrassingly readable" markup language RHTF, and was last updated on 2023 Jun 17.

s.27