Farey Addition
Farey tree
Robert P. Munafo, 2023 Jul 23.
An operation performed on two rational numbers (expressed as reduced fractions) in which you add the numerators together and add the denominators together (or, as your children might say, adding fractions the way you always wanted to!1). The standard name for this operation is mediant, and it's also called "freshman addition". The name "Farey addition" is from Robert Devaney, see 2.
The result of a Farey addition is always somewhere between the two original fractions.
If the two original fractions have no fraction between them with a smaller denominator (example: there is no fraction between 1/3 and 1/2 whose denominator is smaller than 2) then the result of the Farey addition is the fraction with smallest denominator between them (in this example, 2/5).
The Farey Tree
The simple fractions (those that are reduced and lie between 0 and 1) can be arranged into a binary tree graph following the rule that each fraction has two children that are computed by performing Farey addition between the parent (on one side) and an earlier ancestor (on the other side), illustrated approximately like this:
1/2 / \ 1/3 2/3 / \ | \ 1/4 2/5 3/5 3/4 / \ / \ / \ / \ 1 2 3 3 4 5 5 4 - - - - - - - - 5 7 8 7 7 8 7 5 . . . (etc.) . . .For example, to get "4/7" in the bottom row we are "Farey-adding" 1/2 and 3/5.
Applications
If the two original fractions are the internal angles (that is, they are each reduced fractions, see relatively prime) of two mu-atoms with the same parent, then Farey addition gives the internal angle of the inner neighbor of those two mu-atoms.
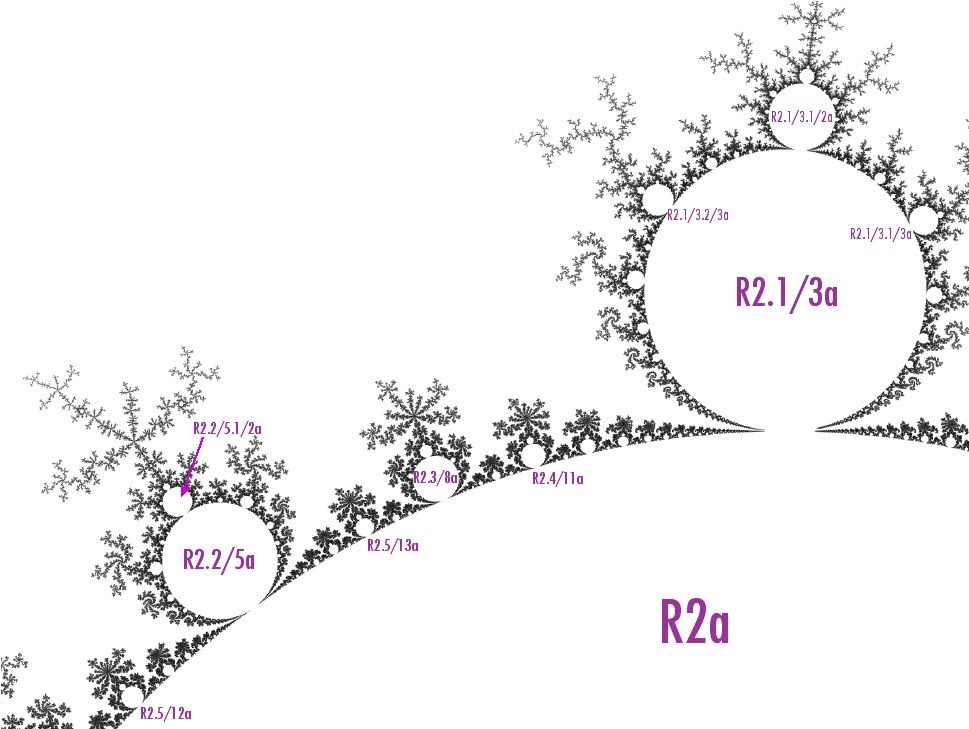
some mu-atoms that serve as examples of Farey addition
In this figure, the two two mu-atoms R2.2/5a and R2.1/3a have internal angles 2/5 and 1/3 (respectively). Their inner neighbor is R2.3/8a, and its internal angle is 3/8, which is the "Farey sum" of 2/5 and 1/3.
Similarly, the inner neighbor of R2.2/5a and R2.3/8a is R2.5/13a. Again, its internal angle 5/13 is the "Farey sum" of 2/5 and 3/8.
There is an efficient algorithm for "finding" a mu-atom with a given internal angle. See binary search for internal angle.
See also smaller neighbor, larger neighbor.
Related Algorithms
Given a mu-atom of interest (the "parent"), it has an infinite set of child mu-atoms all of which have a period that is a multiple of the parent's period. The enumeration of features article discusses how to count how many there are of each eligible period.
The Lavaurs algorithm provides a way to locate all mu-atoms of all periods, and gives a geometrical relationship between them; however it does not make obvious the discinctions of which ones have the same parent and which are e.g. islands in attached filaments.
Sources
1 : The phrase "adding fractions the way you always wanted to!" is from Robert Devaney's How to Count and How to Add.
revisions: 20090510 oldest on record; 20120406 add Devaney credit and mediant link; 20120414 link to binary search for internal angle; 20120416 add figure; 20230615 link to related algorithms 20230723 link to bibliography
From the Mandelbrot Set Glossary and Encyclopedia, by Robert Munafo, (c) 1987-2024.
Mu-ency main page — index — recent changes — DEMZ
This page was written in the "embarrassingly readable" markup language RHTF, and was last updated on 2024 May 10.
 s.27
s.27