Rubik's Cube and other Cuboid Puzzles (page 3) at MROB

First page . . . Back to page 2 . . . Forward to page 4 . . . Last page (page 6)

Solution:

1. Hold the puzzle so the proper Up color shows in the center square of the 3×3 face, and the proper Front color is in the middle edge facing you.

2. Get the corners into place just as you would on the 1×2×3 (see above). Start with one corner and work your way around either clockwise or counter-clockwise so you can put the next corner in place without disturbing the ones already solved.

3. Now either two or four edges are flipped over.

3a. The two edges at F and R can be flipped with R²F² R²F² R²F² (6f). To flip a different pair of edges, the same moves will work with R and F changed to any two adjacent sides. (Note that this is an algorithm from the 1×2×3, and also serves as a useful operator on the 2×3×3 and larger puzzles).

3b. If all four edges happen to be flipped, the 1×3×3 superflip, R²F²L²B² F²L² F²L² (8f) will set them right in 8 turns. (This happens to be the only position on a 1×3×3 that needs 8 moves to solve).

1×3×4

Ola Jansson made the first 1×3×4 in 2010; pictures here.

1x4x4

Ola Jansson also made the first 1x4x4 in 2010; pictures here.

Permutation-Only 2×2×2

This is a 2×2×2 that is limited to moves that keep two opposite colors (white and yellow in the pictured examples) on the U and D faces. In other words, L², F², R² and B² are allowed but L, F, R and B are not. Enforcing this on a normal 2×2×2 requires a complex physical modification, but it can be simulated easily with a bandaged 6×6×6 whose two middle layers are ignored:

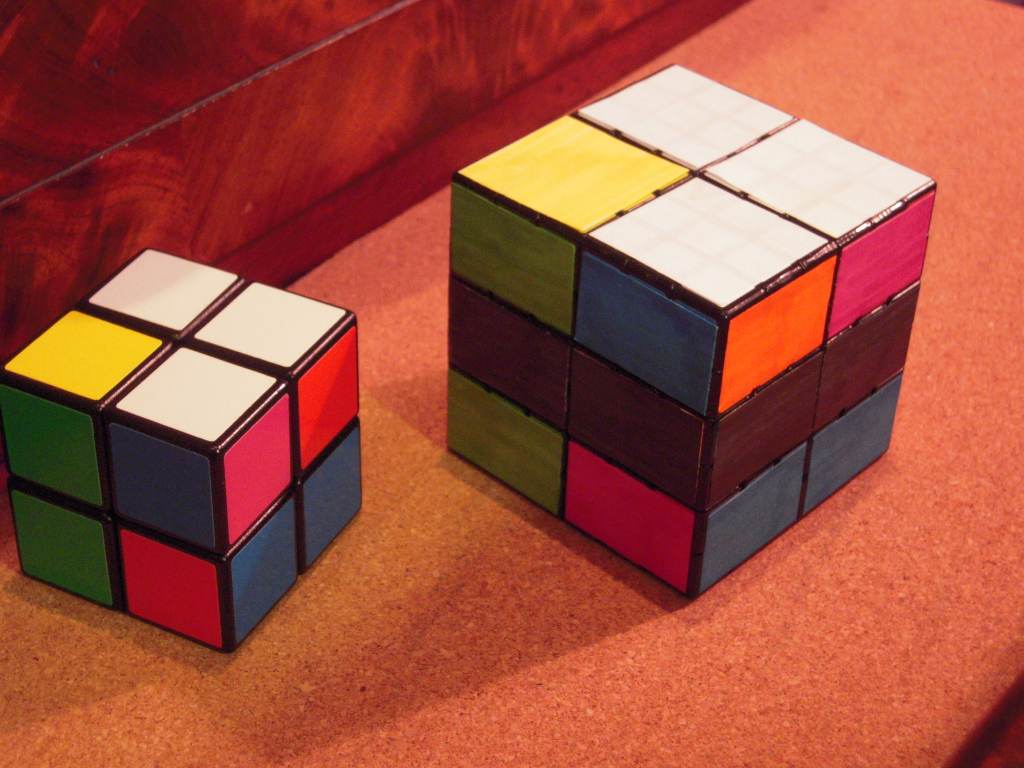
The restricted 2×2×2 can be emulated by bandaging a 6×6×6

The permutation-only 2×2×2 is the most important subgroup of the 2×2×2 because its algorithms are applicable to many other cuboids with a similarly restricted move set, including the 2×2×3, the 2×2×4, the 2×3×3, the 3×3×4, and any other cuboid in which two (but not all three) of the dimensions are equal. It also appears as an intermediate step in the 4-stage Thistlethwaite algorithm for solving the 3×3×3.

Computer searches show that the maximum number of moves required to reach any position is 13, and the average is 8.85. Some of the 13-move states are pair swap algorithms identical to the "dedge flip" on the 2×2×4, 3×4×4, 4×4×4 and similar swaps of two edge pieces on larger cubes. Here is an example, which exchanges URF with DFR:

UR² UF² U²R² UR² D² F² U' R² D (13f)

The same manipulation can be accomplished on the normal (unrestricted) 2×2×2 in 11 moves:

R' F R² D F' D' F' R² F' R D (11f)

Number of Combinations : Any single pair swap can be performed (see above), so the 8 pieces can be permuted into any position. There is no fixed orientation, so we can assume that one piece (say the DLB piece) is already solved, or turn the whole puzzle until it is. That leaves 7!=5040 combinations for positioning the other 7 pieces.

Solution : I present two methods, both are designed to demonstrate a lot of algorithms which are applicable to larger puzzles. If you learn all these algorithms you can solve many puzzles more efficiently.

Method 1 : This method uses reduction to the 1×2×2 case by grouping the pieces into U-D matched pairs.

1. Match each U piece with its corresponding D piece.

1a. Turn D until at least one piece on the U layer matches a piece on the D layer, or if that is not possible turn R² first, then turn D until at least one pair matches.

1b. Put the solved pair at BL, then look at the piece in UFL. Find its matching piece. Turn R² if necessary to put it on the F face. (If the matching piece is already in DFL, you have another matched pair already).

If the piece is at UFR, use U' F² U F² U (5f).

If the piece is at DFR, use R² U F² U' (4f)

1c. Get a third (and therefore, the 4^th) matched pair. Turn the puzzle so the two matched pairs are on the back. If the other two pairs are not matched up yet, one of the following will be required (notice they are each other's inverse: both algorithms are a 3-cycle of the pieces in UFR, DFR and DFL):

To match UFL with UFR, use U' R² U' R² U F² U' R² U² (9f)

To match UFL with DFR, use U² R² U F² U' R² U R² U (9f)

2. Solve as far as possible using the algorithm for the 1×2×2 above (in other words, alternate R² and F², and stop when it is as solved as it can get).

3. Solve the rest of the way.

3a. To swap the two FL pieces with the two FR pieces, use R² U' R² U² F² U' R² (7f).

3b. To swap URF with DRF, use U R² U F² U² R² U R² D² F² U' R² D (13f) (This is essentially the same algorithm as the 13-move dedge flip for the 2×2×4, 3×3×4, 4×4×4 and larger cubes.)

Method 2 : This method starts by getting the top and bottom faces to a solid color.

1. Get all U pieces onto the U layer.

1a. Usually you can get at least 3 onto the top with intutive moves.

1b. To get the rest onto the top layer, turn D to put a desired piece in DRF, and turn U to put an unwanted piece in URF, then exchange UFR with DFR using @R²D'R²DR² (5f).

2. Match each U piece with its corresponding D piece.

2a. Turn D until at least one piece matches.

2b. To 3-cycle (UFL → UFR → URB), use F² U' R² U R² F² U F² U' R² (10f)

2c. To swap the pair at UFL and UFR, use U' R² U F² R² U R² U' F² U F² (11f).

3. Solve the rest of the way.

3a. To swap the two FL pieces with the two BR pieces, use R²F²R² (3f).

3b. To swap the two FL pieces with the two FR pieces, use R² U' R² U² F² U' R² (7f).

2×2×2

Although factory-made 2×2×2's are readily available, this size has also been a popular custom project.

Here is the paper 2×2×2 cube by creptrbot: watch

As described in one of the old Scientific American articles, the 2×2×2 can be built from a 3×3×3 by affixing large extensions to each of the corners. Exactly one of the corners should also be attached to the three adjacent edge pieces (to prevent the center slices from turning partway and jamming further turns on another axis). Before the keychain 3×3×3 cube was available the result was a very large 2×2×2, such as the one seen here.

Here is a Java emulator: http://www.speedcubing.com/CubeSolver/MiniCubeSolver.html

My work with the 2×2×2 goes back to 1982, and is discussed extensively above. I will just summarize a few key points here:

All results regarding achievable positions on the 2×2×2 apply directly to the 8 corners of a 3×3×3, 4×4×4 or any larger NxNxN puzzle.
Because there are no fixed pieces, the first corner can be solved by turning the whole cube around. The rest can be arbitrarily arranged, giving 7!=5040 position combinations; they can also be rotated but only by an aggregate total that adds up to a multiple of 360^o, so there are 3⁶ rotation combinations; the total number of combinations on the 2×2×2 is therefore 7!×3⁶ = 3674160.
When 180^o turns are allowed, any position can be reached from any other position in 11 turns or less, and the average is 8.76.
One of the "local maxima" patterns is the 4-checkerboards pattern, R² U² R² F² (4f).

Solution: The 2×2×2 is the smallest puzzle that involves corner orientation.

1. Get 4 corners in place. I just use a typical "first layer solve" technique for this.

2. Orient the corners. I hold the cube with the good side (from step 1) up as the U face, and use R' D' R D' R' D² R D² (8f), which turns the DRF, DRB and DLB corners counter-clockwise. The goal is to get the D color on all 4 D facelets. Use the algorithm one or more times to accomplish this.

3. Position the last two corners. Turn the cube over and perform U one or more times until two corners are in place (this is always possible). Then use one or more of the following to solve the rest (any one of these can be used to solve any situation, but sometimes less efficiently).

3a. If there are two adjacent corners out of place, hold the cube so they are at UFL and UFR and do R² F R F' R² F U' R U F² (10f).

3b. If there are two opposite corners out of place, hold the cube so they are at UFL and UBR and do R² U' R F' R' U R² U F U F' (11f)

3c. You may also wish to perform a 3-cycle on corners. To cycle (ULF → URF → URB), use F'LF' R² FL'F' R² F² (9f)

(My normal method, because it is easiest to remember, uses only 1, 2, and 3c of the above)

2×2×3

This puzzle is fairly easy to make from a keychain 3×3×3 and cubies from a full-sized 3×3×3. My own building tutorial is here, and a video summary of the procedure is here.

There are two ways to bandage normal cubes to emulate the 2×2×3. Both are pictured here. On the left is a 4×4×4 bandaged by 4→1+2+1→3 on the vertical axis and by 4→2+2→2 on the other two axes. The other is a 3×3×3 with black stickers on all centers and eight edges. This latter cube is not really a "bandaged" cube, because it does not physically enforce the 2×2×3 dimensions of the puzzle you're emulating, but if you wish you can use a piece of tape to secure the U center to the UF and UL edge pieces, which will at least partially prevent illegal turns (although it will do little to prevent your 3×3×3 from getting its invisible edges scrambled when you manipulate it like a 2×2×3). Here are the two emulated cubes, in an equivalent scrambled state:

A real 2×2×3, and two ways to emulate it

Locked Shapeshifted State : When half (a 2×3 portion) of a 2×2×3 is turned just 90^o, the puzzle is in a "locked shape-shifted" state like that shown here:

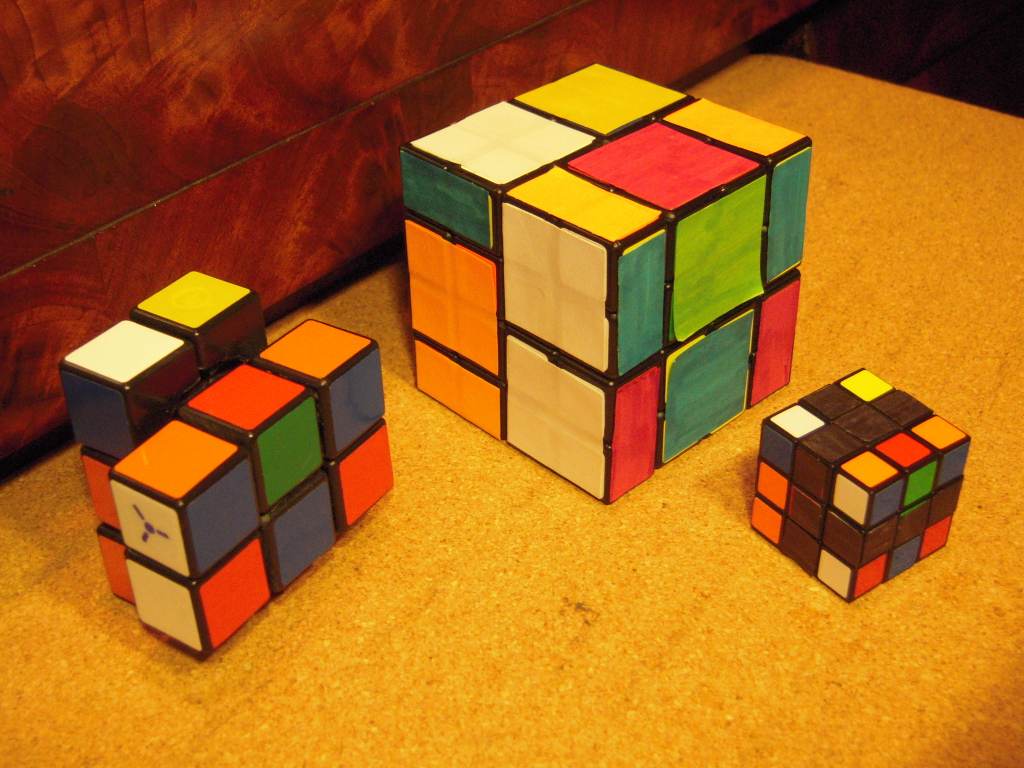
The 2×2×3 in a locked shape-shifted state

From this position, nothing can be done except to un-do the 90^o turn or to continue it for another 90^o. This restriction is properly simulated by the bandaged 4×4×4 cube in the photo, but not by the blacked-out 3×3×3.

Number of Combinations : There are 8 corner pieces and 4 edge pieces. One of the edge pieces can be assumed to be solved, and the other 3 edges can be arranged arbitrarily, as can all 8 corners. As with the 1×2×2, the edge pieces can be flipped but not independently of their position. The orientation of the corner pieces is also fixed by their position. This gives a total of 8!×6=241920 positions.

Alternatively, we can assume one of the corners remains fixed (in this discussion that will be the DLB corner). The other corners can still be arranged in any position, giving 7!=5040 for the corners. The central slice can now be turned, allowing the 4 edge pieces to be put in any of the 4!=24 combinations, however the 1×2×2 constraint on orientation still exists: when a pair of edges is swapped by F² or R², both pieces' orientations are also flipped. If a piece is an even number of steps from "home", it will be upright, otherwise upside-down. However, since the layer can be rotated, you could turn the layer 90^o and have all your pieces 1 step from home and still upright. Alternately you can move them all one space clockwise (with a flip because it is one space from home) and then do a single turn to get all 4 edge pieces flipped in their home position — this is the 2×2×3 superflip operator, U' R² U₂' U² R² U₂' U² R² U₁₂' (9f). Either way, this effectively doubles the number of combinations in the central layer to 24×2=48. Combined with the corners, this gives the same answer, 48×5040=241920 positions.

My computer analysis shows that any position can be reached from any other in at most 14 turns. The average is 9.74.

It may seem a bit counterintuitive that this puzzle has more pieces than the 2×2×2 but far fewer positions. The reason is because of the fixed orientations of the pieces. Every corner piece has three hidden "faces": two of these touch neighboring corners, and the third touches a neighboring edge. This third side will always touch an edge, no matter how you turn the puzzle — so the corners are always oriented the same way. Another way to see this is that the white and yellow facelets on the top and bottom will always be on either the top or the bottom.

By contrast, the corner pieces on a 2×2×2 (or any true cube-shaped puzzle) have greater symmetry — all three of their sides touch a side of another corner (and on a 3×3×3, every side of a corner touches a side of an edge piece). This greater symmetry gives each piece more choices on how to be oriented.

Notation: We will imagine the puzzle is positioned as pictured above, showing the U, F and R faces. The U face is the one with 2x2 squares, and the other two faces are 2x3. We'll use standard 3×3×3 Singmaster notation: F², R², B² and L² for 180^o rotations of the 2x3 slabs, and U, U', U², D, D', D² for the top and bottom. In addition there is the central slice or "equator". U₂ will signify turning this slice 90^o clockwise as viewed from above, and U₂', U₂² have similar interpretations.

The top four pieces are corner pieces, named (starting from the back-left) UBL, UBR, UFR and UFL. Directly below these are the middle pieces, also called edge pieces or edge-centers: BL, BR, FR and FL. Below these are the bottom corners, DBL, DBR, DFR and DFL.

Commutator Algorithms

The 2×2×3 cannot (in general) be solved by someone who knows how to solve the 3×3×3 Rubik's Cube, because the lack of 90^o turns on four of the faces makes almost all of the 3×3×3 algorithms impossible. This offers an opportunity for otherwise experienced cubist to derive new algorithms from scratch. Here is an example of how to create an algorithm to swap a pair of corners:

First, we want to find a way to change just one piece on a side. We're trying to swap corners, so we need to find a way to replace one of the corners on the top (U) layer with another piece. Here is one way to do that:

put one pair on the bottom : R²
break up the pair : D R²
move the piece that is currently on the bottom : D
bring it back to its proper place : R² D² R²

The above sequence of 7 moves changes just one piece on the U layer, the one at URB, by replacing it with the piece that was formerly at DRB. It also messes up the pieces on the bottom layer.

Imagine now that you have done these 7 moves, and then you un-do them by performing the opposite turns in the reverse order (R² D² R² D' R² D' R²). This will put everything back the way it was.

But imagine instead that you turn the U face before un-doing the 7 moves, and then turn U back. This will almost put everything back — except, instead of returning the DRB piece to where it belongs, another U piece will be put there instead. Also, the piece originally at URB will be returned there, but when we turn U again at the end, the URB piece will be turned to, and end up where that other U piece came from.

This sequence, which has a total of 16 turns, is called a commutator. It is an algorithm to move 3 pieces, leaving everything else unchanged:

R² D R² D R² D² R² U² R² D² R² D' R² D' R² U²

The commutator has a structure, or a sort of symmetry to it, which is normally expressed as P Q P' Q'. The P section is the set of 7 moves that moves URB to the bottom layer. Q is a single 180^o turn of the U face. P' is the reverse of P, and Q' is the reverse of Q, which happens to the same as Q because all 180^o turns are their own inverse.

This algorithm performs a 3-cycle of corners: it moves URB to ULF, it moves ULF to DRB, and it moves DRB to URB. Once we have a 3-cycle algorithm, we can make it into a different algorithm by bracketing it with set-up moves. For example, if we add the moves L² D' L² to the beginning, then the ULF and ULB pieces are moved to DRB and ULF, respectively. if we then do the 16-move algorithm, and then un-do the setup moves, we have an algorithm to 3-cycle the pieces at URB, ULF and ULB:

L² D' L² R²DR²DR²D²R² U² R²D²R²D'R²D'R² U² L² D L²

This algorithm moves ULB to ULF, which moves to URB, which moves to ULB. It is particularly useful, because if we follow it with just one more U, we have a pair swap of the pieces at ULF and URF.

Solutions: To demonstrate the technique of reduction, which is used extensively in solutions for the 4×4×4 and larger regular cubes, I present two solutions for the 2×2×3 that work by "reducing the problem" to a smaller, previously-solved puzzle.

Method 1 : We start by pairing up corner pieces.

1. Get the first pair. Usually there is already a pair of corners that are matched. Otherwise, look for a corner piece on the U side with a neighbor on the D side, turn U and D to put them at ULF and at DRB, then either R² or F² will bring them together (depending on which half of the pair is which — just try R², and if they aren't matched up properly, then do R²F²).

2. Turn the cube so the good pair is at ULB-ULF. Now look at the piece at URF and find a second piece that would match it if that second piece were at ULF. Put that second piece at DBL and do R²D. Now there is a second matched pair at DBL-DFL. (If the needed second piece is at URB, get another piece into URF, e.g. by doing R² or DR², and try again.)

3. Hold the cube so the good pairs are at ULB-ULF and at DBL-DFL, and look at the remaining four corners. These might already be paired up, but if not, there are two possibilities:

3a. The third pair are both on the top, but paired backwards: do U to put them at UFL-UFR, then do R² F² U R² U' F² U R² D' F² (11f) Now look at the bottom, if there is still one mismatched pair (which will be at DRF-DLF) do F² to put it on top, then repeat the algorithm.

3b. One of each pair is on top. Turn D until the piece matching UFR is at DFR, then do U² R² U R² U² F² U R² U² F² U F² U (13f) After this, the other pair will be together but they might be paired backwards; if so use step 3a to fix it (re-orienting the cube if necessary).

4. Pair up the center-edge pieces. The two edge pieces at FR and BR can be swapped with R² U² R² U² R² U² (6f).

5. Now all the pieces are in pairs. Turn U, U₂ and D as needed so there are three matched pairs on the left and three on the right.

6. Use the method for the 1×2×3 to join the pairs into complete layers of 4 pieces each. (Note that in my 1×2×3 solution I hold the puzzle with a 2×3 side facing up.).

7. All three layers are complete. The puzzle can now be solved like a 1×1×3.

Method 2 : This method for the 2×2×3 works by layers.

1. Pick a side with at least two of the Up color, and hold the puzzle so that side is up. To get the rest of the pieces with the Up color to the Up layer: turn D to put one of the needed pieces at DFR, and turn U to put an unwanted (Bottom) piece at UFR, then do F² D F² D' F² (5f). Repeat if needed. This step also puts all the D pieces on the bottom.

2. Put top and bottom pieces in proper positions:

2a. Find a pair to swap on the upper layer and turn U to put these two at UFL and UFR. Find a pair on the bottom that needs to swap and turn D to put them at DFL and DFR. Then do R² U F² U² R² U R² (7f).

2b. If there is only one pair of corners left to swap, use one of the following:

Adjacent pair: hold the puzzle so the pair is at UFL and UFR, and use R² F² U R² U' F² U R² D' F² D (11f)

Diagonally opposite pair: hold the puzzle so the pair is at ULB and UFR, and use U F² U² R² D' F² U² R² U F² U² R² (12s)

2c. An algorithm to cycle the 3 corners (URF → URB → ULB): L²D R²D'R²DR² U' R²D'R²DR² U D'L² (16s)

3. Fix the middle layer.

3a. Start by turning U₂ to get at least one edge to agree with the top and bottom layers.

3b. If none of the edges can line up (with both of its colors at the same time) use the superflip: U' R² U' D' F² U' D' R² U' (9f)

3c. To fix the rest of the middle layer, turn U₂ to put two edges that need to be swapped at FL and FR, then use F² D² F² D² F² (5f). Repeat if necessary.

4. All three layers are complete. The puzzle can now be solved like a 1×1×3.

First page . . . Back to page 2 . . . Forward to page 4 . . . Last page (page 6)

s.27