Rubik's Cube and other Cuboid Puzzles (page 5) at MROB

First page . . . Back to page 4 . . . Forward to page 6

3×3×3

The original Bűvös kocka (Hungarian, "Magic cube"), invented in 1974 and exported for a while by specialty shops before being mass-marketed by Ideal Toy Corporation.

The 3×3×3 emulated on a 1989 5×5×5 and a modern Eastsheen 4×4×4

Construction of the original Ideal Toy Corp. 3×3×3

Here is a Java emulator: http://www.speedcubing.com/CubeSolver/CubeSolver.html

Solution: Here is my current 3×3×3 solution technique, derived mainly from the algorithms I developed and learned from friends in 1981 and 1982.

1. Get the first layer. I used to do this by the intuitive technique, but I now start with the white cross just as speedsolvers do, because I hope to teach myself some of Fridrich-style F2L algorithms soon.

1b. Position edges on the middle layer. I sometimes flip a pair as well.

2. Position and orient the other 4 corners. I hold the now-complete F2L facing up, and use the corner algorithms from my 2×2×2 technique (see above), all of which move edges on the D layer only.

2a. To cycle (DRF → DLF → DLB), use F'RF' L² FR'F' L² F² (9f)

2b. To exchange the corners at DFL and DFR, use L² B D B' L² F U' F U F² (10f)

2c. To exchange the corners at DRF and DLB, use L² U' R F' R' U L² D B D B' (11f)

2c. To rotate the corners at DRF, DRB and DLB, use R'D'RD' R'D²RD² (8f)

2d. If there are exactly two corners rotated properly, I position them and a third corner at DRF, DRB and DLB, and use the previous algorithm once or twice until there is exactly one corner oriented properly, then turn D until that corner is at DFL and use the algorithm again one or two more times.

3. Position the remaining edges. 3a. To cycle (UF, FR, FL), use R₂F R₂'F² R₂F

R₂' (7s)

3b. To swap two pairs (UR, DR) and (UF, DF), use (R²F²)³ (6f).

4. There may be one or two pairs of edges to flip.

4a. To flip edges at DF and DR, use R₂'D²R₂D'R₂'D R₂D² R₂'D²R₂D R₂'D'R₂D² (16s).

4b. To flip edges at UF and UB, use (R₂U)² R₂U² (R₂'U)² R₂'U² (12s)

The Centerless 3×3×3 "Void Cube"

The Void Cube is a 3×3×3 with no center pieces or core — it has actual physical holes going right through the middle in all three dimensions. It works just like a 3×3×3, due to an ingeneous mechanism that is even more surprising to those who understand how a normal 3×3×3 mechanism works.

The void cube can be emulated on a 3×3×3 simply by covering the centers with black:

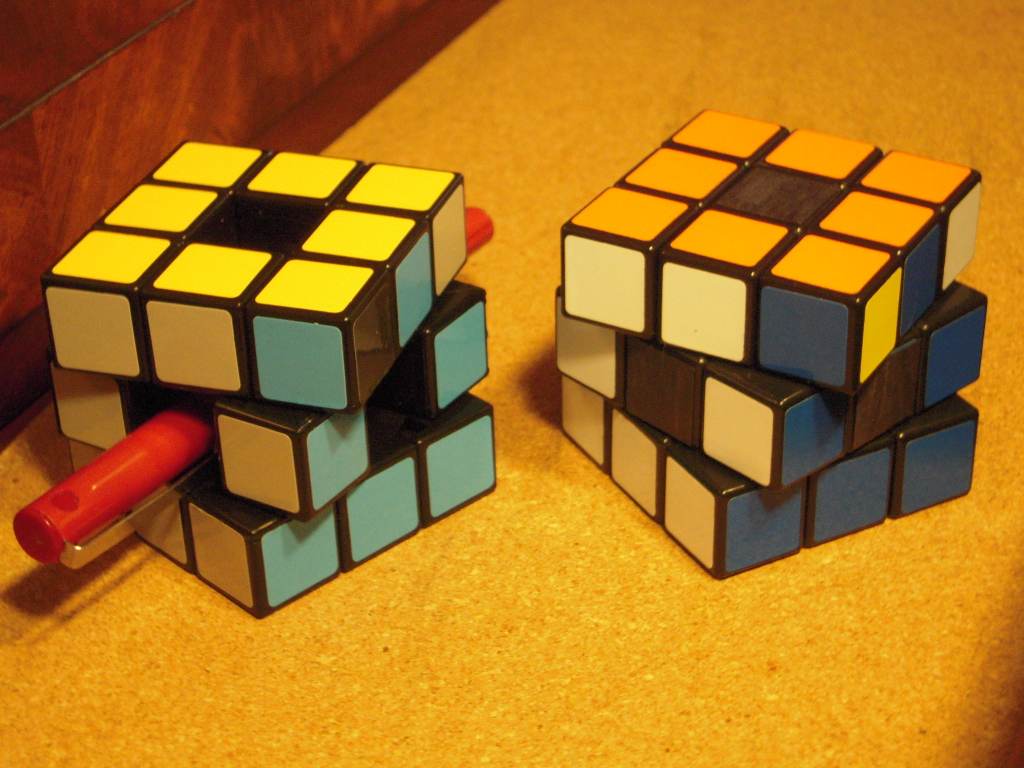
Void Cube emulated by a 3×3×3

As shown here, apparent parity errors can arise on the void cube: the entire cube is solved, except for a single swapped pair of corners. A single swapped pair of edges is also possible.

Number of Combinations: Assuming a single corner as a fixed reference, the corners alone have the same number of combinations as the 2×2×2, which is 7!×3⁶ = 3674160. Because any center slice turn creates an odd permutation of edges, the edges can be permuted into any of the 12! combinations. As on the normal 3×3×3 cube, they can also be flipped in pairs, giving 12!×2¹¹ = 980995276800. Combined, the Void Cube has 7!×3⁶ × 12!×2¹¹ = 3604333606207488000 ≈ 3.6×10¹⁸ combinations.

Solution: I use corners as the orientation reference when solving a Void cube.

1. Get the first 4 corners in place using normal intuitive "first layer" techniques.

1a. (You might also choose to get the first layer edges too, as it does no harm to do them now.)

2. Solve the other four corners using the algorithms from the 2×2×2 above.

3. Solve the rest of the edges as far as possible.

3a. I use the edge movement algorithms shown in the following discussion of the 3×3×3.

3b. Try to notice a pair-swap parity error as soon as possible. It is best to try to notice this when there are 4 left to put in place, then check if the 4 edges are out of place in a cycle of 4, rather than as two swapped pairs. If this happens, there will definitely be a parity problem. If you reach a point where there are exactly 3 edges out of place, then there will definitely not be a parity problem.

4. Fix edge parity, if any. This is done by making any single slice turn: L₂, R₂, F₂, B₂, U₂, or D₂. If possible, choose one that will cause one of the edges to be moved to where it belongs. The rest can then be solved with one or two 3-cycles or a double-pair swap.

3×3×4

As of summer 2009, the 3×3×4 is in commercial production; it can also be emulated easily by a bandaged 4×4×4:

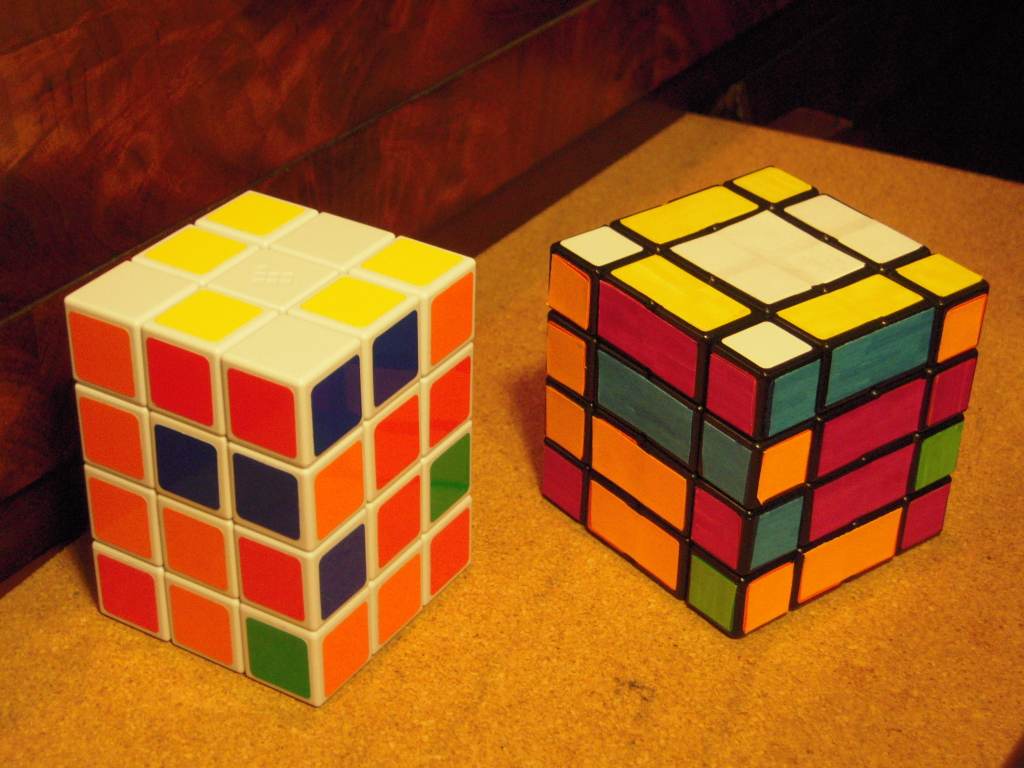
A real 3×3×4 can be emulated by a 4×4×4

Watch Tony Fisher's 3×3×4; another video here. There are photos here.

Here is another that also shows part of the internal mechanism. This video shows a 3×3×4 being assembled from a kit.

Since this cube has two odd-numbered axes, a full six-face checkerboard pattern is possible (so long as you do the two odd-number axes first: F₂²R₂²U₂₄² works, but F₂²U₂₄²R₂² and U₂₄²F₂²R₂² put stripes on two and four faces respectively)

The corners of this puzzle are equivalent to the permutation-only 2×2×2. Like the 2×2×3, it cannot be turned further after one of the side faces (L, F, R or B) is turned 90^o:

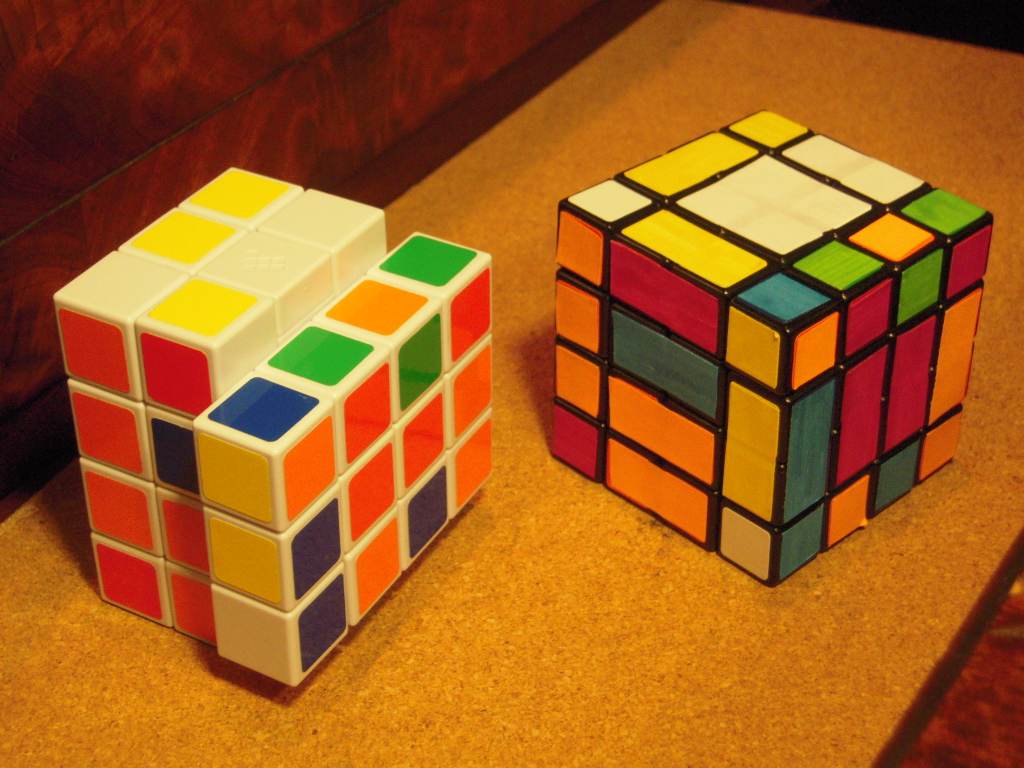
The 3×3×4 in a locked position

This cube has eight single edge pieces, located on the 3×3 faces, and four pairs of double-edges that behave like the edges of the 4×4×4, located on the 4×4 faces. The algorithm for flipping a double-edge on the 3×3×4 is also the best known algorithm for erforming the same task on a 4×4×4.

This puzzle can emulate the 2×3×3 by bandaging the 1^st layer to the 2^nd and the 3^rd to the 4^th.

Notation: This puzzle has the ability to emulate a normal Rubik's Cube with the restriction that four faces can only be turned by 180^o turns. When emulating a 3×3×3 this way, the 3×3×4 is oriented with the 3×3 faces Up and Down, and the four 3×4 faces as the Left, Front, Right and Back faces.

In addition to the previously used notation for face turns, I use two more turns for the middle two layers. If the U layer is the 1^st layer and the D layer is the 4^th layer, then U₂ means turning the 2^nd layer in the same direction as U, and D₂ means turning the 3^rd layer in the same direction as D. The 2 subscript refers to the 2^nd layer away from the face that is named by the letter, so U₂ means Up, layer 2. We can also use a 3 subscript, to refer to the 3^rd layer away from the face, and so U₃ means the same as D₂'.

Pieces on the U and D layers can be named the same way as on the 3×3×3 cube, but the pieces on the other two layers need more unique names. There are two face-center pieces on the F face, named F_U and F_D. The two edge pieces between the F and R faces are FR_U and FR_D. They can also be referred to as RF_U and RF_D. If an edge piece moves from one location to the other, the name can be chosen to make it clear the piece has also flipped: for example, if FR_U and FR_D exchange places, we say that FR_U moved to RF_D and FR_D moved to RF_U.

Number of Combinations: If bandaged like a 2×3×3, the puzzle can be put in the same number of combinations as that puzzle, which is 8!×8!/4 = 406425600. The inner two layers have distinguishable edge pieces (corresponding to the corners on an inner 2×3×3) and 4 pairs of indistinguishable centers. In addition, parity of the 2^nd and 3^rd layer edge pieces is linked to that of the corners, so it is impossible to get an odd permutation of one without having an odd permutation of the other. The same relationship holds true for the centers and the 1^st and 4^th layer edge pieces, however the ability to make an invisible swap of center pieces nullifies this restriction. (These points is is described near the end of this assembly video.) This makes the number of combinations (8!×8!)/(4×4×2) × 8!×8!/2⁴ = 5161930260480000 ≈ 5.16×10¹⁵.

Solution: Here is the solution I came up with right after gettng my 3×3×4:

1. Pair up the center edge pieces into dedges.

1a. Use R², F² and/or U₂ to get at least one pair matched (you can usually get two).

1b. Use L², F², and/or R² to get two edges that need to be matched into the FL and FR columns.

To join the pair at FL_U and FR_D, and also join the pair at FL_D and FR_U, use R² D₂ R² D₂' (4s)

To join the pair at FL_U and FR_U, and also join the pair at FL_D and FR_D, use U₂ F² D₂ B² D₂' F² D₂ B² D₂' U₂' (10s)

2. Solve the dedges and corners as on a 2×2×3.

2a. You might be left with one or more dedges in position but flipped:

Double dedge flip: To flip the dedges at FL and FR, use R² D₂² U₂ F² U₂' D₂' F² D₂' R² (9s)

To swap the two edge pieces at FR_U and FR_D, use U₂ R² U₂ F² U₂² R² U₂ R² D₂² F² U₂' R² D₂ (13s)

3. If necessary, match the U and D centers with the corners by doing F₂² or R₂².

4. Solve the F,R,B and L centers.

To exchange both of the F centers with both of the B centers, use (D₂²R₂²)²) (4s)

To 3-cycle (F_D → F_U → R_U), use D₂' F₂² D₂ F² D₂' F₂² D₂ F² (8s)

5. Solve the U and D edge pieces.

To exchange (UL, DL) and (UR, DR), use (R²F₂²)² (4s)

To exchange (UF, UB) and (DF, DB), use (D²F₂²)² (4s)

To exchange (UF, DF) and (UR, DR), use (R²F²)³ (6s)

To 3-cycle (UR → UF → UL), use F² U' R²F²R² U² R²F²R² U' F² (11s)

To 3-cycle (UR → FD → DR), use (R²DR²D')⁵ (20s)

Single pair swap: To exchange UL and UR, use F² D₂² R² F² D₂² F² R² U² D₂² F² U² F² U² (13s)

Other Algorithms

Pure dedge flip: to swap the two edge pieces at FR_U and FR_D without affecting the rest of the cube, use D₂' R² D₂ R² U₂' R² U₂² F² D₂ F² U₂' R² F² D₂² F² (15s). (This algorithm is also applicable to the 4×4×4.)

3×3×5

5×5×5 emulating a 3×3×5

Here is a video of Tony Fisher's 3×3×5 in action. here are some photos. It is made from an Eastsheen 5×5×5 cube core, bandaged into a 3×3×5 (using the 5→2+1+2→3 bandaging on two axes, like that pictured here). The result has 9+8+8+8+9=42 externally visible pieces. This bandaging and the design of the Eastsheen 5×5×5 allow the edge and corner pieces to be cut fairly deeply, allowing for a modification like that used for the 2×2×3.

The 3×3×5 is the smallest three-axis shapeshifting puzzle with odd dimensions.

The surprising thing with this puzzle is that, when rotated 90^o into a non-rectangular shape, the central three slices still rotate and the puzzle behaves like a 3×3×3 with extra cubical protrusions. This makes the puzzle appear to be just a 3×3×3 with extra cubes glued on, until you return it to the pure rectangular shape and discover that now the 1^st and 5^th layers turn too.

This behavior is duplicated exactly by the bandaged version shown here. Since none of the bandages connect to any central slice, the central three layers can always rotate with respect to each other.

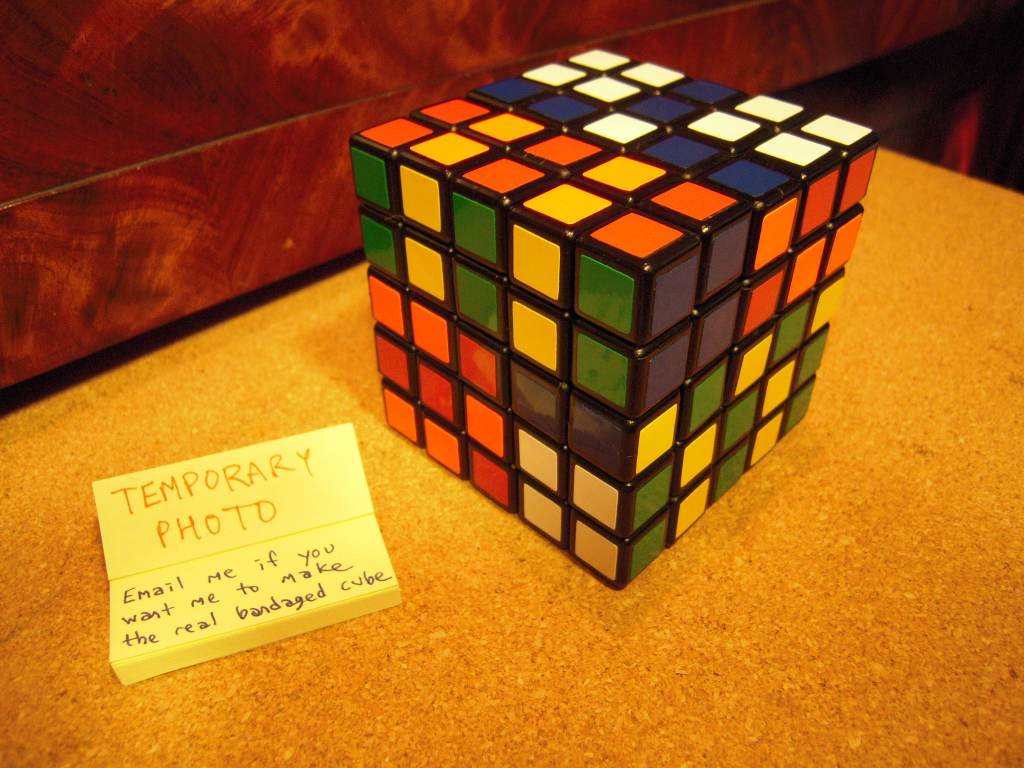
bandaged cube in a pattern corresponding to a shapeshifted form of the real 3×3×5

A real cube with proportions similar to the bandaged 5×5×5 is pictured here.

Therefore, by necessity, solving it involves first solving it as if it were a 3×3×3, then dealing with the 1^st and 5^th layers. As seen in his solving video, some of Tony Fisher's algorithms for restoring these layers involve temporarily putting the cube into an odd shape.

Here is another 3×3×5 construction; according to the author this one was made from 3×3×3 cubes, presumably adding the 1^st and 5^th layers by a technique similar to the 2×2×4. It is also able to shape-shift after 90^o turns.

This is the first in a series (not yet complete as of this writing) on how to build one.

Number of Combinations : As with the 2×2×4, we can consider the outermost layers (the 1^st and 5^th layers) to be decorations on a 3×3×3, with 8!×8! combinations (this differs from the 2×3×3 because different orientations can be distinguished by using the face centers as a reference). The central three layers are like a 3×3×3, however 4 pairs of "edge" pieces are now center pieces that are indistinguishable from each other. These pieces do permit making what appears to be an odd permutation of the corners and the other (normal) edges. So the number of combinations for those 3 layers is 8!×3⁷×12!×2¹¹/2⁴. This gives (8!)³×3⁷×12!×2¹¹/2⁴ = 8789360691018252209356800000 ≈ 8.7894×10²⁷.

3×3×6

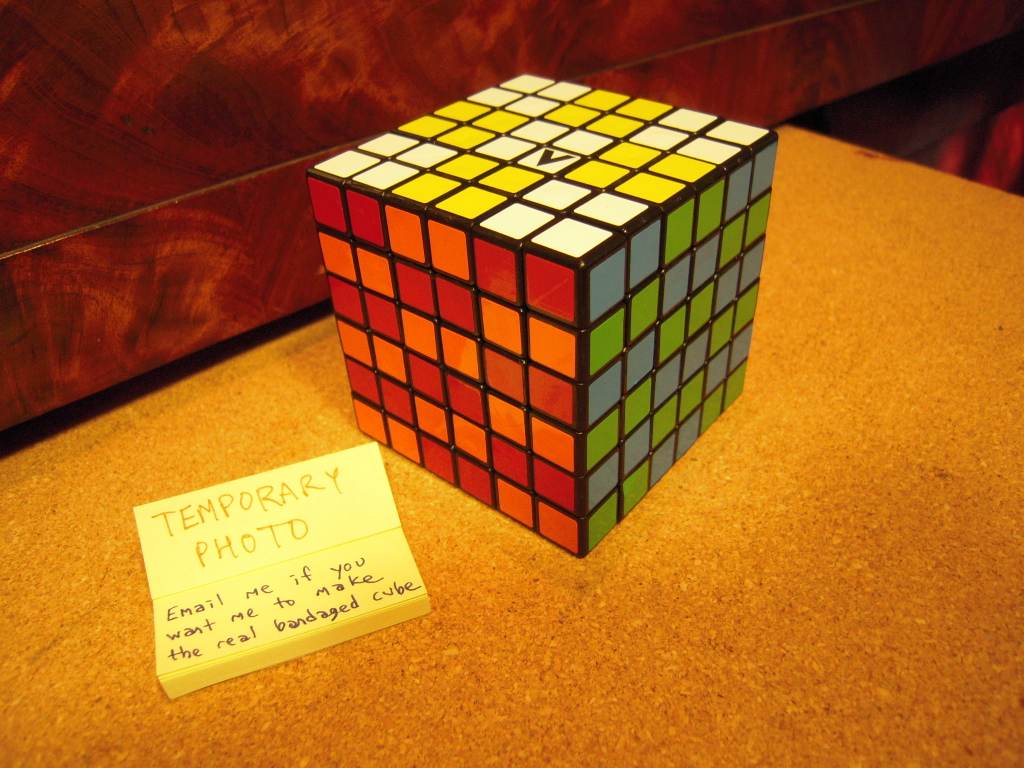
6×6×6 emulating a 3×3×6

Note that with the bandaged version shown here, impossible patterns can be created (similar to shapeshifted patterns, see the 3×3×5, but shapeshifting cannot occur in a real cube because the midplane of the 6-number axis would cut the center slice of cubies on either of the 3-number axes).

As with the 3×3×4, a full six-face checkerboard pattern is possible, provided you do the two odd-number axes first: F₂²R₂²U₂₄₆².

http://www.youtube.com/watch?v=iRD2zKh_24s&feature=related

http://www.youtube.com/watch?v=0eYqfi12-ck&feature=related

3×3×7

This video shows a fully functional 3×3×7 in action; here is another.

3×4×4

"Jin/neochronius" has made a 3×4×4; photos are here. A video of it in action is here.

3×4×5

6×6×6 emulating a 3×4×5

This puzzle can shape-shift. Hold it with a 3x5 side facing up, then do (for example) U F₁₂² U₁₂.

This page shows a design for a 3×4×5 that was made with CAD-CAM prototyping tools, the results are seen here and here.

3×5×5

This video shows a 3×5×5 in action. It shape-shifts, because like the bandaged-emulated version, the central 3×3×3 part is able to function even after one of the 3x5 layers has been turned only 90^o.

4×4×4

In most 4×4×4 solutions, emulating a 3×3×3 on a 4×4×4 is used as the basis of a large portion of the solving time. The edges are grouped together and the cube (or perhaps a portion of it, such as the first 3 layers, or everything but the centers) is solved as if the 4×4×4 were bandaged to emulate a 3×3×3 or a void cube.

However, on the 4×4×4 it is also possible to flip a single dedge and exchange a single pair of dedges, two things that cannot be done on a 3×3×3.

Notation: I use my extended Singmaster piece labeling and move notation from 1982, described above.

Solution: Here is my current 4×4×4 solution technique, most dating back to May 1982 when I worked it out for myself.

1. Find a center that already has most of the same color on the 4 center pieces; if there is none do a few moves to create one. I use this as the reference "Up" side during the edge-pairing.

2. Pair up edges

2a. I start by positioning four edge-pairs around the "equator" (U₂ and U₃ slices) chosen in such a way that a single U₂ or U₂' turn will create three matched pairs. Then I "store" these matched pairs on the U or D face, and continue finding more pairs to match up. 8 pairs can be created this way, and then a 9^th pair can be created from what remains on the "equator".

2b. To pair up the last few pairs of edges, I use the following algorithms:

Place two pairs to be fixed in the UL and UR positions. The edge at UL_B should match the one at UR_F. If the pair at UR is oriented the wrong way for this to work, flip it over with something like R'UF'U'.

To exchange UL_F with UR_F, use R²F₂ R²F₂' R² (5s). (NOTE: This is just my original 1982 algorithm B²R₂B²R₂'B² moved to different faces)

The pair at UL is now matched; if there is another broken pair repeat the previous steps again.

3. Solve like a 3×3×3 (ignoring the centers). If you know how to solve the Void Cube, this is essentially the same thing, although you may get a single flipped edge at the end.

3a. My method is here; the important point being that I solve all the corners before the last several edges.

3b. Because there is no reference for the centers, you may get a single swapped edge pair (or corner pair, if you solve the corners last) just like on the void cube. For a corner swap, perform a single quarter-turn of a face that contains the swapped pair of corners, then use 3-cycles to fix the 3 corners that are now out of place and as many edges as possible; a swapped pair of edges will be left.

4. Fix edge "parity". As discussed above, one of the following may be necessary:

4a. To exchange the UR and DR dedges, use F₂²R² F₂²R₁₂² F₂²R₂² (7s)

4b. To flip the dedge at FR, use U₂ R² U₂ F² U₂² R² U₂ R² D₂² F² U₂' R² D₂ (13s)

5. Put the centers in place. I use many variations on the following "commutator" algorithms, all of which fit a pattern which you will probably see if you try each of them on a cube (hint: apply tiny sticky-notes to each of the named facelets, or pairs of facelets in the 3^rd example, do the algorithm, and watch where they move.) Notice that two center facelets can be solved at once this way.

L₂U₂L₂' U L₂U₂'L₂' U' (8s) : 3-cycle of (R_UF → U_LB → U_LF)

R₂'D₂'R₂ U² R₂'D₂R₂ U² (8s) : 3-cycle of (R_DB → U_FR → U_LB)

L₂U₂₃L₂' U² L₂U₂₃'L₂' U² (8s) : Cycles 3 pairs (R_F → U_L → U_R)

More Algorithms: Here are some more algorithms for the 4×4×4, most of them of the "pure" variety that produce no side-effects (except perhaps exchanging identical centers on an otherwise-solved cube).

To cycle the edges (UF_L, FU_R, UB_R), use R₃'UF₂ D'R₃UR₃'DR₃U' R₃'F₂'U'R₃ (14s)

Dedge flip without altering centers: D₂'R²D₂R² U₂'R²U₂² F²D₂F²U₂' R²F²D₂²F² (15s)

A few more can be found here.

First page . . . Back to page 4 . . . Forward to page 6

s.27