Building the 2x2x3 Cuboid Puzzle

2×2×3 Building Made Easy
This page shows the simplified technique with which I built my 2×2×3 "slim tower". (If you just want to solve a 2×2×3, look here.)
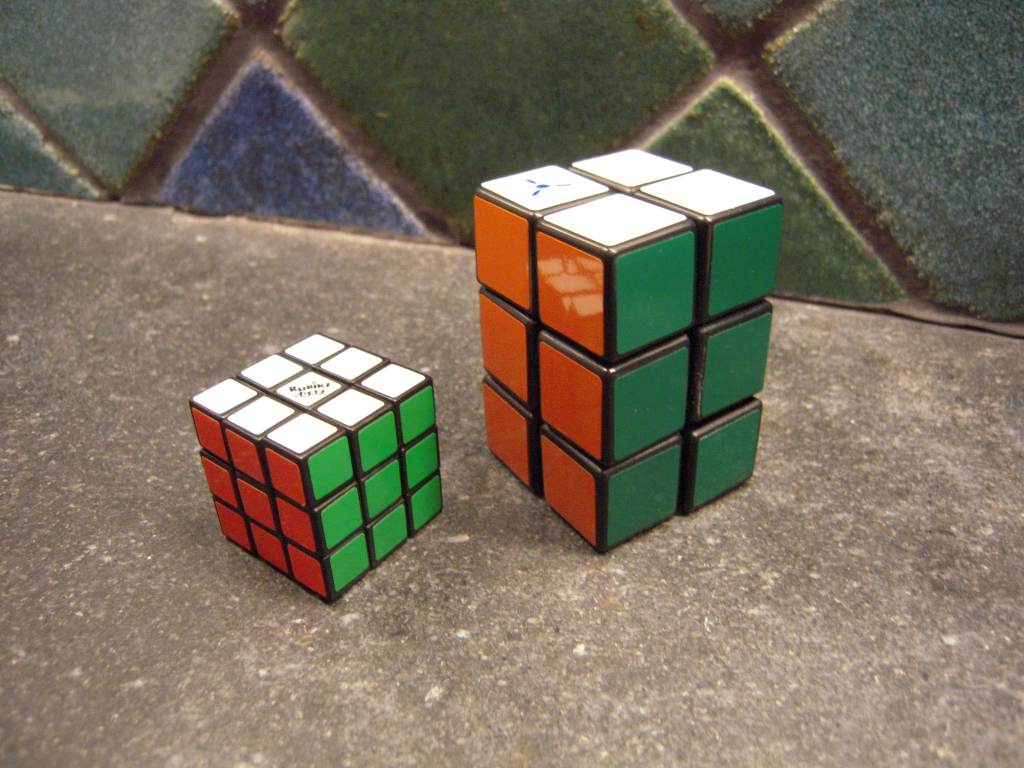
My 2×2×3 next to a keychain 3×3×3
I built the 2×2×3 shown here in a couple of days. The basic design originates with Tony Fisher of Ipswich UK, and can be seen in this article. It was a fairly easy project and my first foray into custom-made puzzles; my (significantly improved) technique for construction is outlined below. Here is my tutorial video:
History
The core ideas behind this method were described by Hofstadter[1], near the end of the article:
Various people have made 2×2×2 cubes, and such cubes may go on sale one day. You can make your own by gluing little three-cornered hats over each of the eight corners of a 3×3×3 cube.
Since then, the same method has been adapted to making the 2×2×3 and 2×3×3, as well as (occasionally) smaller puzzles like the 1x2x3.
Particularly notable among such work is that of Tony Fisher, who has been doing cube modifications at least as far back as 1982 (siamese cubes, see [2] page 10). He refined the basic technique of attaching "little hats" to the pieces of a Cube to create the "maxi cube" (a 3×3×3 enlarged to roughly twice its original size in each dimension). Once this has been figured out, it is a fairly simple matter to adapt the technique to create the 2×2×3 "slim tower" and the 2×3×3 (a Magic Domino with colored stickers instead of domino spots).
Fisher's original designs for these three modifications are described on this webpage. Some specific examples and discussion by other recent builders can be found here and here.
Overview of My Technique
Here is a diagram and scale models that show a modified "keychain" 3×3×3 cube that serves as the core and the 4 full-size 3×3×3 edge pieces that are the first to be attached to it. On the model of the modified cube, the green lines represent glue where 4 pieces are fused together, and the red lines show where parts of pieces have been cut away:

Models of core and 4 edge pieces
In order to position the edge pieces properly, two dimensions A and B need to be measured:
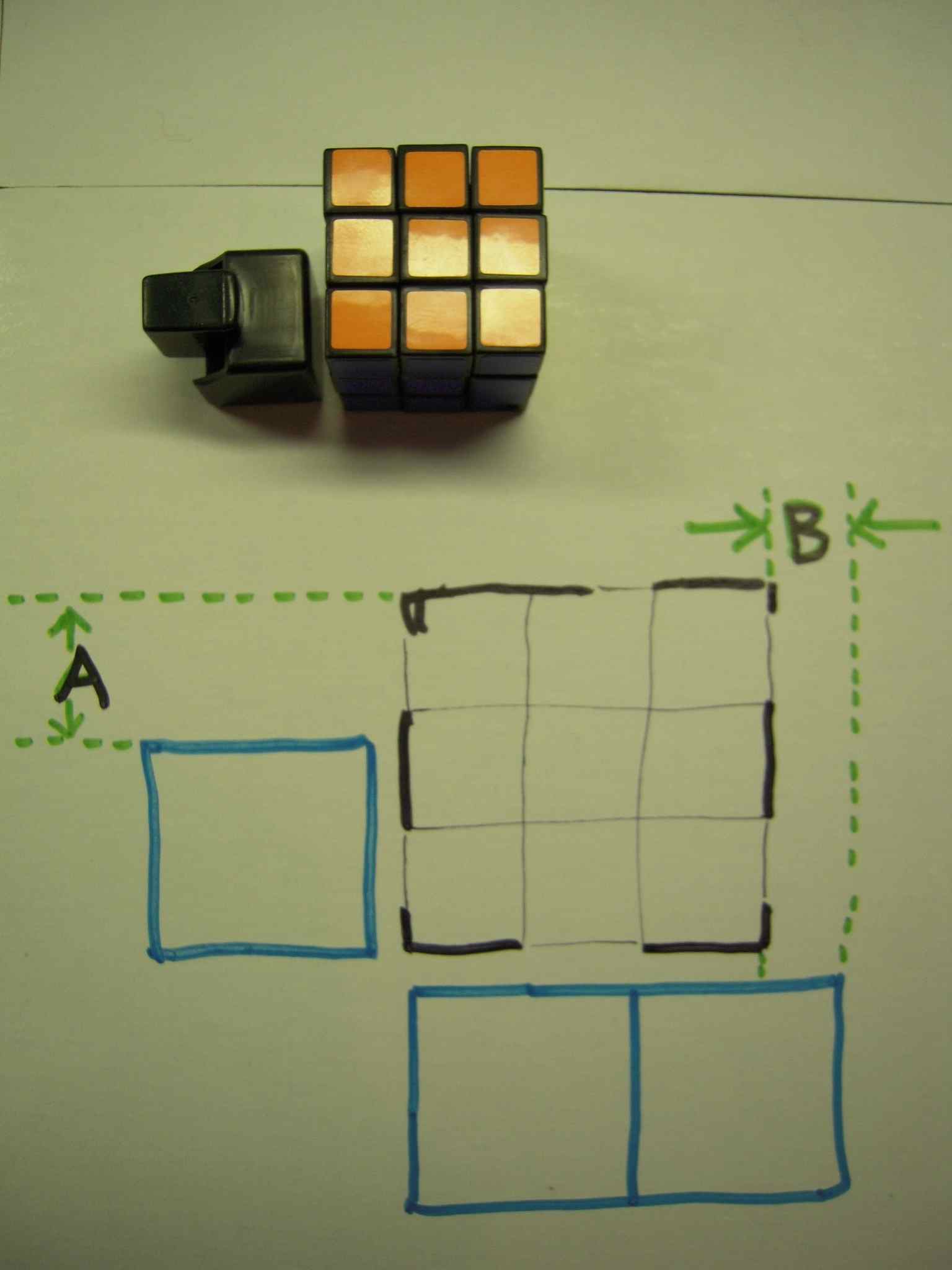
The critical dimensions A and B
These dimensions are used to align the edges as illustrated here:

How the first 4 pieces are aligned
The 4 edges are aligned in all 3 dimensions all at once using a set of eight sticky-note pads arranged as shown here:

The "pinwheel" arrangement of sticky-note pads
Once the edges are in place, and using the same setup, it is a simple matter to attach the corners.
Here is the completed puzzle with a few pieces taken out:

The 2×2×3 partially disassembled
Here are all the pieces of the puzzle I built: One corner with the core mechanism and two internal edges glued together, 6 normal corners, one removable corner in two pieces with a screw, 6 internal edge pieces, and 4 normal edge pieces:

The 2×2×3 fully disassembled
Step-by-step Instructions
Note that the center pieces on the keychain cube are a little higher than the rest. In order to do our measurements, we need the top and bottom of the keychain cube to be flat. Disassemble the keychain cube, sand down 2 opposite center pieces, these will be the top and bottom sides. Look at the edge and corner pieces and locate which way the "hollow" part is. Reassemble the cube with all the hollow parts of the edges on the top (U) layer facing down, and the hollow parts on the bottom (D) layer facing up.
Before doing any more modifications to the keychain cube, create sticky-note pads whose thickness is exactly equal to dimensions A and B. This is done by creating an arrangement like this:
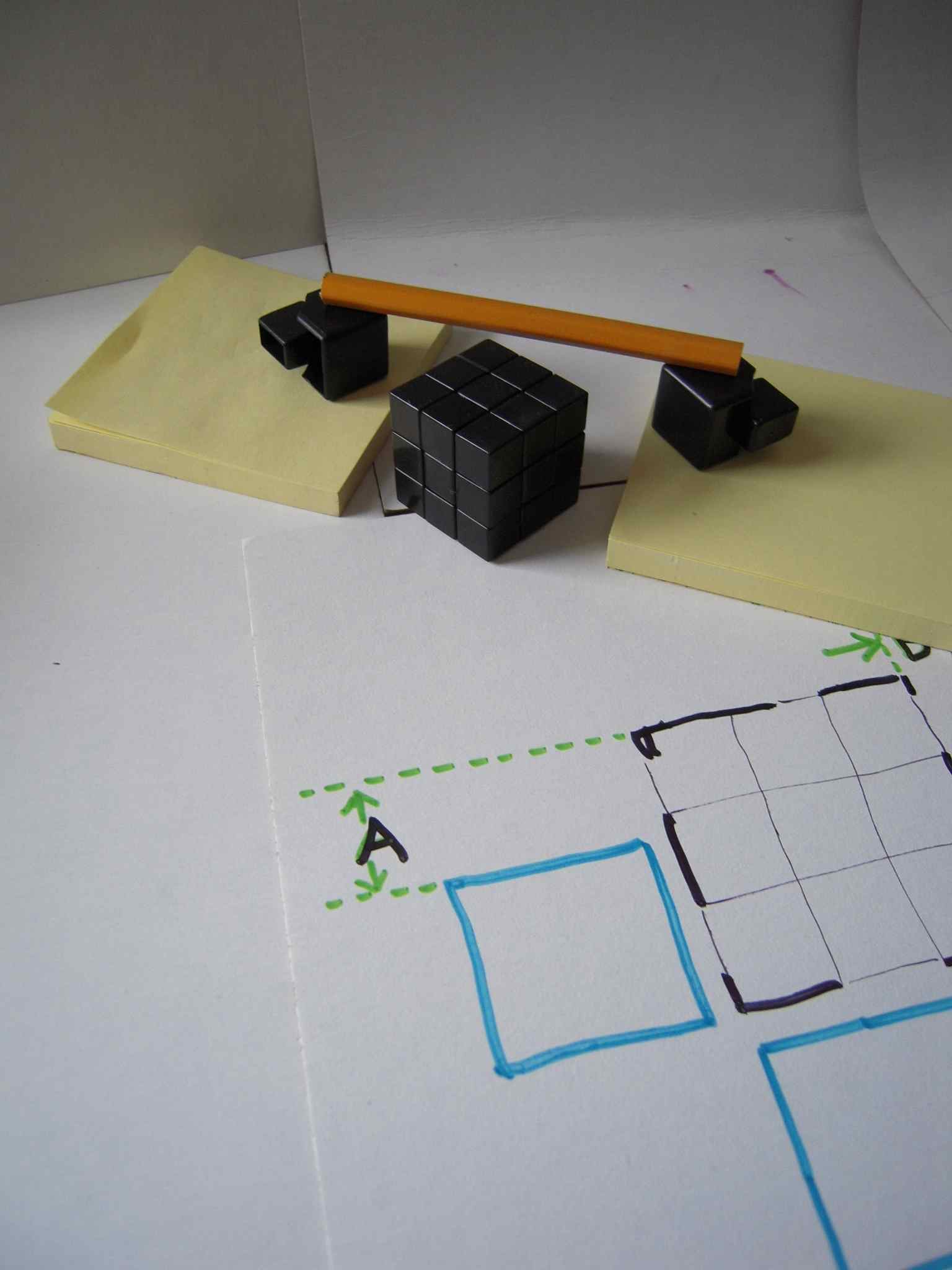
How to measure dimension A
Adjust the height of the pads of paper by adding and/or removing sheets. Get it so the keychain cube just barely slides under the pencil without knocking it off. Make sure both pads are the same height each time you measure — this can be done by comparing both to a third pad whose thickness is also adjusted at the same time.
When you have done this, both pads are of height A. Take one of them and divide it in half into two pads. Move sheets from one to the other until they are the same height. Now you have two pads of height A/2. Do this with the other pad so you end up with four pads of height A/2.
Using a similar technique, measure the difference between the height of two full-size edge cubies and the height of the keychain cube. This time you need to have the two full-size cubies on the table and the keychain cube sitting on a single sticky-note pad:
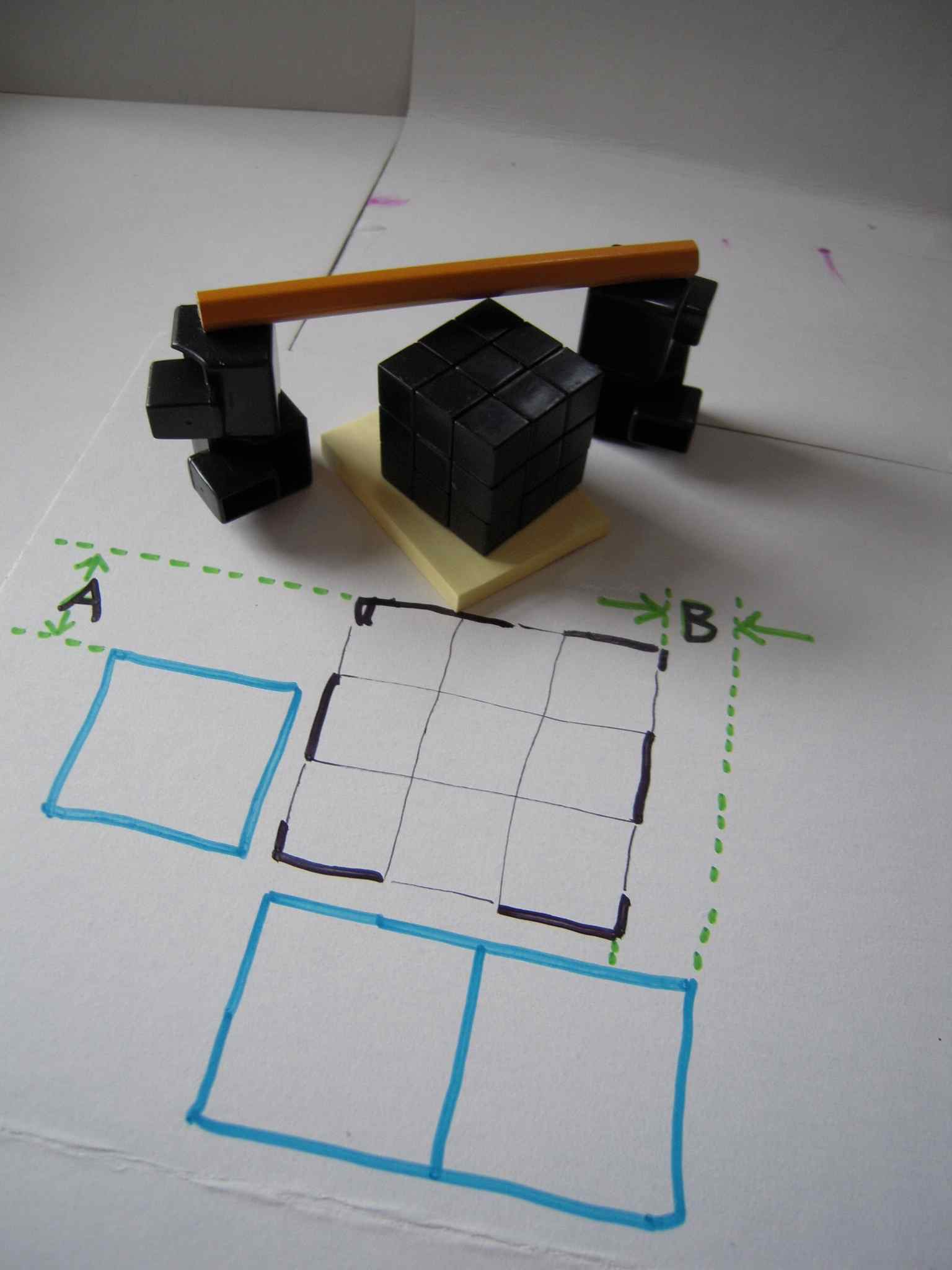
How to measure dimension B
This is dimension "B". Again, it needs to be divided in half. This time you need to keep only one of the resulting B/2 pads.
A total of 9 sticky-note pads are used: four of thickness A/2, one of thickness B/2, and four that are about half the height of one of the full-size edge pieces.
A jig will be made of two overlapping pinwheel shims. The bottom layer looks like this, with the central square space being exactly the size of the keychain cube:

Building the jig (step 1)
Here is a schematic view from the top looking down. C represents the central hole; A/2 is the thickness of each of the four sticky note pads:
+------+ | A/2 | +-----| | | A/2 |---------+ | | C | | +---------| A/2 | | |-----+ | A/2 | +------+Now stick the B/2 sticky-note pad on the side of the keychain cube. This will provide the horizontal positioning for the second layer. Start the second layer like this (note the thickness of these pads does not matter):

Building the jig (step 2)
Turn the keychain cube 90o and then add the next sticky-note pad:

Building the jig (step 3)
Continue all the way around until it looks like this:

The finished jig
The spaces on the inside form a two-layer terraced arrangement of two concentric square wells, one that precisely fits the keychain cube "core" and one that precisely fits four of the full-size cube pieces that are glued to it. It holds all the pieces in just the right places, with the sole exception of possible rotations of the 3 layers of the small 3×3×3 cube (which is handled below).
Modifying the Keychain Cube
Once the jig is assembled, the central core can be modified. Cut down the eight U and D edge pieces, cut away at the eight corner pieces, and reassemble. Test to make sure it still turns well. Fix any turning problems by removing pieces and sanding off any surface irregularities. Then glue the DLB corner and the DL and DB edge pieces to the D center. (See my pictures above; another drawing of the modified core is here.) After the glue dries, reassemble.
Modify the full-size corner and edge pieces in the normal way (as shown here and here and here). You might also cut the "caps" of the corners into a quarter-arc shape which could be glued back into place after the puzzle is complete, to make the corners look more pure. (In my project, it turned out that there wasn't quite enough clearance for these to fit in without further cutting away at the small inner corner pieces, and I decided not to bother with it. Whether that happens for you will depend on the type/brand of mini and full-size 3×3×3 cubes you used for this project.)
To secure the X and Y axis rotation planes, turn the core's top layer 45o to ensure the three layers are all flat. To secure the Z axis rotation for the central slice, slide small strips of a hard, thin material (I use tiny bits of aluminum soda can) in the vertical cracks in the bottom layers. Try to fit 4 strips, one on each side. These have to be very small to not interfere with the edge pieces that are being glued on, and you also have to have a bit sticking out so you can pull them out later. Here is a picture:

The core prepared for gluing on the edges
You can just make out the tips of two of the aluminum strips near the left side of the core. The top layer is turned 45o.
The four edge pieces can all be glued at once, using a small bit of putty. First tape them together like this, and make sure they all sit evenly on a flat surface:

Tape the 4 edge pieces together
Then, using 4 small blobs of epoxy putty or some other sticky and stretchy type of adhesive material, attach the 4 full-size edges to the core, and then carefully work the assembly into the mold until all the pieces sit level and snug within the mold:

Glue hardening on the 4 edge pieces
Wait until the epoxy putty has hardened enough to handle the puzzle, and take it out of the "mold". Remove the thin strips, and use the moves (F2R2)3 to test alignment. While doing this, look for consistent spacing and alignment between the pieces that have just been glued on.
If it looks good, disassemble and add more epoxy, super-glue or whatever seems appropriate to make the newly glued pieces stronger.
At this point you might also choose to fill the rest of the core's edge and center pieces with epoxy putty and let them cure at the same time. This is generally done to make the puzzle heavier and can also sometimes help it turn more smoothly. (I chose not to do this for my first model because it was working just fine).
Gluing on the corners is a very similar process. Before doing the corners it is good to fill in the central hole of the mold like this — a rectangular piece of several layers of paper or cardboard. This will help the corners sit level:

Extra insert for the corners
The core can be prepared in exactly the same way (see the photo above), at least for the first 4 corners. For the last 4 corners it might be a good idea not to use the little aluminum strips because they can be hard to remove afterwards. (I used a more elaborate solution: a removable corner, described below)
Glue each set of corners on by putting the 4 corners in the "mold" with the rest of the puzzle on top, like this:

Adding the first 4 corners
After each set of 4 corners is attached, test the alignment by turning the puzzle in different ways, and when you are satisfied, add more glue to make the new pieces stronger.
I built my puzzle with one "removable" corner that is in two pieces connected with a small screw; this required some extra steps which you can work out on your own. The 2×2×3 can be disassembled easily without this, but I think the removable corner made it easier for me to build the puzzle, because I could use it to reach inside and remove the little aluminum strips after the last 4 corners had been attached.
Other Ways to Build the 2×2×3
Here is the first part of the turorial by "neochronius" that got me interested in developing this improved process.
Large 2×2×3's can also be made from a bandaged and extended 4×4×4. This video outlines two different ways.
Here is Kenneth Brandon's 2×2×3 being scrambled and solved, with a few pictures of the building process.
Footnotes
[1] Douglas R. Hofstadter, Magic Cubology, column for the March 1981 issue of Scientific American. Now available as chapter 14 of Hofstadter's 1985 book[3].
[2] David Singmaster, Cubic Circular, issues 3-4, summer 1982. Now available here.
[3] Douglas R. Hofstadter, Metamagical Themas, book collecting several articles from the Scientific American column of the same name, BasicBooks (1985), ISBN 0-465-04540-5.
Rubik® and Rubik's Cube® are registered trademarks of Seven Towns, Ltd. These pages are not endorsed or sponsored by the owner(s) of any trademarks.
This page was written in the "embarrassingly readable" markup language RHTF, and was last updated on 2010 Nov 09.
 s.27
s.27