Rubik's Cube and other Cuboid Puzzles

Robert's Cubehacking Pages
Contents:
This page is organised in a roughly chronological manner, because I am trying to document my own history with the cubes. I tried to develop my own solution techniques and this resulted in non-optimal, but nevertheless interesting, solutions.
After the "chronological" section is a collection of notes that are specific to each cuboid size, like 2×3×4. There are solution techniques, but none is particularly fast; instead I prefer to use smaller cuboid solutions as building blocks for larger ones. For example, the 2×3×3 solution includes "solve it like a 1×3×3" as a middle step, and that in turn invokes the 1×2×3 solution. The 2×3×3 could be solved in far fewer turns using a Fridrich-like Speedcubing method.
Those unfamiliar with the basics of these puzzles or how they work can read the Wikipedia entry on Rubik's Cube.
1981: The 3×3×3 Cube
This is the original "Rubik's Cube" from the early 1980's. I learned about it from the first Hofstadter article on the topic (in Scientific American, March 1981); I and a few friends at school got the cubes that spring.
The article introduced the "Singmaster notation" (also described in [1]) which is fairly obvious and easy to learn (and therefore has persisted). In this notation the 6 sides of the cube are named after the first letters of the English words Up, Down, Front, Back, Left, and Right. A letter by itself means to turn that side of the cube clockwise by 90o (and only one "layer", that is, turning 1/3 of the cube while holding the other 2/3 still). A 180o turn is indicated with a superscript 2, thus F2 means to turn the front side 180 degrees. A 90^[o} counter-clockwise turn is indicated with a "prime" or single quote character, so L' means to turn the left side "away" from you.
Singmaster's notation also names the pieces of the cube (or more accurately, the positions they occupy when solved). Each piece is named with 1, 2 or 3 letters corresponding to the color or colors that appear on that piece (but with letters still indicating the sides of the cube, not the actual names of colors). Thus, for example, the corner piece in the upper-right-front corner is caleld URF, and the edge piece along the left side of the front face is called FL. The order of these letters is important too: FL and LF are the same piece, but in opposite orientations. A corner piece has three possible orientations, like URF, RFU and FUR. By convention the three parts of the corner piece are named in clockwise order (as if viewed with that corner pointing directly towards you).
My work in 1982
I augmented the Singmaster notation in two ways:
- A letter inside brackets means to rotate the whole cube. For example, [R] means turn the whole cube 90o clockwise as seen from the right side.
- I needed a way to describe a middle "slice" of the cube in a more abbreviated way than (for example) [R]R'L. I decided to use Rs for this. This is notably different from Singmaster's "Rs", which means RL'.
First Solving Methods
I began by trying to work out as much of the puzzle as I could on my own. This resulted in an initial solving method that used five algorithms of my own design/discovery plus one from another student, most of them rather long and cumbersome to use. Using these I could solve the cube in about 6 minutes.
If you're actually trying to solve a cube right now,
go to my Updated Table of Algorithms
|
* These 4 algorithms were used in my original solving technique, which took about 6 minutes.
+ These 6 algorithms were used in my later 3-minute solving technique.
Apple ][ Cube Emulator
Around the same time I was developing the 3×3×3 technique, I created this emulator for the 3×3×3 cube that ran on an Apple II. The coloring reflects that of the original Ideal Toy version of the cube, which has blue opposite white, yellow opposite green, and red opposite orange, with yellow/red/blue in clockwise order.

My Apple II cube emulator
The 2×2×2 Cube
This puzzle came out in the summer of 1982 under the name "Rubik's Pocket Cube", also by Ideal Toy Corp. The present-day "Rubik's Ice Cube" and the "Junior Cube" are physically equivalent. Solving is equivalent to just the corners of a 3×3×3 cube. You can swap a single pair of corners, but the rotations must add up to a multiple of 360o.
Notation is similar: R, F, U, etc. indicate turning one side (half of the puzzle) clockwise 90o. There is no fixed orientation because there are no centers, and a move sequence like RL' moves the whole cube without changing its pattern.
I got the Pocket Cube as soon as it was available. I didn't do much with it except try to find a pretty pattern similar to the Pons Asinorum (checkerboards on all six sides). I did not find one, but did discover the four-checkerboard pattern produced by (for example) F2R2F2U2.
The 4×4×4 Cube
The 4×4×4 puzzle also became available in 1982, under the name "Rubik's Revenge", again by Ideal Toy Corp. It became available on the east coast of the U.S. before the west coast. (Bernard S Greenberg reported that the puzzle was available for $15 at Games People Play in Cambridge MA, in a message to the Cube-Lovers at MIT-MC mailing list on May 13th.) I bought mine on May 21st, at the Tech Coop shop at M.I.T. Since I was a high school student with no contact with anyone else who had this puzzle, I developed my own notation and solving algorithm. I explain how I did this in this video tutorial.
Extended Singmaster Notation
For the 4×4×4 cube, I added to the existing Singmaster notation for the 3×3×3 cube in a way that accommodates the 4×4×4 and anticipated future 5×5×5 or larger puzzles.
Turns
R = Rotate the rightmost layer (1/4 of the cube) clockwise as seen
from the right side
R1 = same as R
R2 = rotate the second-to-rightmost layer (again, 1/4 of the cube)
clockwise as seen from the right
R12 = Rotate R1 and R2 layers together (i.e. turning the
right half of the cube)
R1234 = Rotate the whole cube, same as [R] (clockwise 90o
as seen from the right, i.e. the D face will become F, and the R
face stays in the same direction.)
R', R1', R2' = Inverse of R, R1, and R2 respectively
(turning a slice in the other direction)
R3 = same as L2'
In addition, for the 3×3×3 cube:
Rs = RL' as used by Singmaster, discarding my earlier use of "Rs" which is now replaced by R2.
Later I added:
Rw = Turn the whole cube 90o along the same axis as an R move. ("w" for "whole cube"; Rw is the same as my older "[R]")
Pieces
UFR = the "up-front-right" corner UF = the "up-front" edge piece (on a 3×3×3) or the corresponding
pair of edges on a 4×4×4.
UFR = the half of UF closer to the right side, i.e. the single UF edge piece that is next to UFR.
U = the "up" center piece on a 3×3×3, or all four U centers on a 4×4×4.
UF = the frontward half of U, i.e. the two U centers that are next to UF.
UFR = the front-right part of U, i.e. the U center that is closest to UFR.
I still use this notation today. It is similar to the Dan Hoey notation[3] and more easily adapted to larger puzzles than the more recent system using lowercase letters.
I decided to pair up the edges first, then solve like a 3×3×3 cube (ignoring the centers) and fix the centers last. As a result I ended up developing algorithms to move the centers without disrupting anything else, and my edge-pairing technique does not bother to preserve the centers. My method was similar to what is now known as the "cage method", except I didn't even solve one center to start.
Munafo's Rubik's Revenge solution technique (from 1982)
1. Pair up the edges. [ 2 edge pair swap: B2R2B2R2'B2 (5s) ]
2. Solve in 3×3×3 emulation mode (ignore the centers, and use the corner pieces to figure out which color belongs on each side).
3. (if necessary) Swap single edge pair: [ (R22B2)2R22 (5s) ]
4. (if necessary) Single edge pair flip [ use (R2BR2'B)4R2 then U2R2U2R2'U2 (26s total) and go back to step 2 ]
5. Group centers in twos, then in fours [ (R2B2R2'B2)5 (20s) and (R22F22)2 (4s) ]
This technique was not too efficient, and took me 25:46, 16:51 and 14:04 the 2nd, 3rd and 4th times I used it.
1989: My 2nd period of work
In 1989 I was living in Boston permanently and decided to take up the Cube again. I bought a second Rubik's Revenge so I would have spare parts (My first had broken twice in the same way, indicating a weakness in the design. Having a second cube gave me spare parts.) {After 20 more years, none of my new cubes have broken, so I suspect the problem was isolated to the early Revenge cubes.}
During this period I added to the notebook I originally used for my 1982 notes, using pages 62-64.
On Feb 13th I created my second computer program, RubikHack. This was a random search of positions on the 2×2×2 cube. I made it to search specifically for a "pons asinorum" pattern. After much searching, in which it only found the 4-checkerboard patterns, I realised that the pattern I sought was impossible.
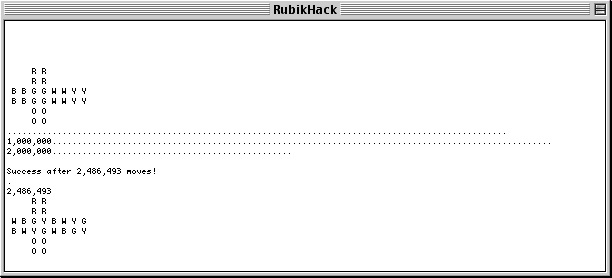
RubikHack reporting a match
Six-checkerboard Pattern on Even Cubes
A pattern analogous to Pons Asinorum is not possible in the 2×2×2 case. This is because the only methodical way to assign faces to colors is to leave 4 corners in their start position, and to move the others as a unit (the corners of a tetrahedron). There are 12 ways to do this (4 corners of a tetrahedron, 3 orientations once the corner has been chosen), but 2 out of 3 are illegal rotations (sum of corner twists is non-integral). The remaining 4 positions are I, F2R2B2D2, D2R2U2B2, and U2F2D2R2.
Naming System for the 4×4×4 Cube
- Corners are named the same way as on the 3×3×3.
- For backwards compatibility with the 3×3×3, the old names for edges are used to refer to two edges of the 4×4×4 taken together. {When solved, they are a matched pair.}
- Edges taken alone are named with a subscript, e.g. URF, URB for the front and back halves of UR.
- Center pieces are similarly named, e.g. ULF, URF, etc.
- When an edge piece moves, it is often flipped by necessity to occupy its new position. This is represented in a manner analogous to Singmaster's notation, e.g. when URF and URB exchange places, it is indicated by (URF, RUB). Note that this is the same as (UR)+, because all of the 3×3×3 notation has meaning in the 4×4×4 as well.
R2'U2R2 U R2'U2'R2 U' = (URB, ULB, RUB)
R2'U3R2 U R2'U3'R2 U' = (URF, URB, RDB)
R2'D'R2 U R2'DR2 U' = (UFR, URB, RDB)
R2F2R2F2' = (ULF, RDB, URB, DRF, RUF) (ULF, RBD) (URF, RBU)
(Useful for "pairing up edges": we desire to move ULF and URB together, which in fact we do. We also put ULB and URF together; so in this sense we are swapping a pair of edge pieces.)
Number of combinations of the 4×4×4 cube
= 8! permutation of corners
× 24! permutation of edges
× 24! permutation of centers
/ 2 combination of permutations must be even
× 38 orientations of corners
/ 3 total orientation of corners must be zero
× 1 (orientations of edges and centers are determined by their position)
/ 24 no particular orientation of the cube is "special"; alternatively
we can assume that the orientation is special by leaving one
corner piece fixed
/ (4!)6 each of the four center pieces of a given color is
indistinguishable
× 2 due to the fact that center pieces are indistinguishable, we can
achieve what appears to be an odd permutation of the other pieces
in the cube by "hiding" a transposition within the center pieces
of one face.
= 7 40119 68415 64901 86987 40939 74498 57433 60000 00000
≈ 7.4012×1045
(24! = 620448401733239439360000)
More algorithms that affect edge pieces
F22R2F22R2F22 = (URF,DRB)(URB,DRF) (also moves 4 centers)
U2'RU2R = (FLU, RBD, RFU, RFD, RBU, DRB, URF, URB, DRF) (4-cycle of corners) (even permutation of centers) {My original handwritten notes omit "RFU" from this list}
R2'D'R2UR2'DR2U' = (URB, DRB, UFR) {This is a simple adaptation of a similar algorithm on the 3×3×3}
R2'D'R2UR2'DR2U' R2 R3'D'R3UR3'DR3U' R2 = (UFR, UFL, DRB)
R2'U2B'R' {This was clearly meant to be the beginning of a longer algorithm}
R3'UF2R3 R3'D'R3UR3'DR3U' R3'F2'U'R3 = (UFL, FUr, UBr)
F2 LF UR3'D'R3U'R3'DR3 F'L' = (DRF, LDF) (lots of centers moved)
U' R3D' R2'D'R2UR2'DR2U' DR3' U = (ULF, UFR, URB)
(The following algorithm uses F2U2L'F2'LF22 to place URF and URB in positions DRF, LDF)
(F2U2L'F2'LF22) F2 LF UR3'D'R3U'R3'DR3 F'L' (F22L'F2LU2F2') = F2U2L'F2'LF2' LF UR3'D'R3U'R3'DR3 F'L' F22L'F2LU2F2' = (URF, RUB) (lots of centers moved) {This is a single-edge-pair flip, although there are much shorter ways to do this and that don't move the centers}
1991: 3rd period of work
4×4×4 "pretty patterns"
(R132U1234)3F1234'R132 — produces checkerboard pattern on 4 faces
There are lots of pretty patterns in the "13-generator" group [R13, L13, U13, D13, F13, B13]. All look like the following figure on each face:
+---+---+---+---+ | a | b | a | b | +---+---+---+---+ | c | d | c | d | +---+---+---+---+ | a | b | a | b | +---+---+---+---+ | c | d | c | d | +---+---+---+---+although the correspondence between one face and another is essentially arbitrary. In fact, the patterns generated by this group correspond exactly to the patterns generated by the [R, L, U, D, F, B] group on a 2×2×2 cube. Warning: If you apply randomly-selected 13-generator moves, you will get a pattern which is difficult to solve within the 13-generator group. Solving a random 13-generator pattern is essentially equivalent to solving the corresponding pattern on a 2×2×2 cube.
1995: 4th period of work
Although the 5×5×5 had been avaialble for a while, 1995 was the first time I saw it in local shop. I bought 5×5×5 cubes on May 25th and June 20th. (The second cube was mainly for spare parts in case the first one broke). I also ordered the book [6].
I began adding a bit to my 1989 search program, with the goal of being able to search for algorithms, but the effort didn't get very far.
As with the 4×4×4, I created my own notation for the 5×5×5. I was able to continue using the notation for moves that I developed in 1982, but augmented it a bit with the RI and Rn forms.
Notation for the 5×5×5
The pieces and positions on the 5×5×5 are named similarly to the 3×3×3 and 4×4×4. I use lowercase subscripts this time, which allows the names for the 4×4×4's pieces to be used in the same discussion as those of the 5×5×5's pieces without ambiguity. Also, the true centers and central edge pieces have the same names as their counterparts on a 3×3×3 cube. Any algorithm from the 3×3×3 cube, when performed on the 5×5×5, results in exactly the same manipulations of these pieces.
The true (non-moving) center pieces are named with a single uppercase letter, as in the 3×3×3. The central edge pieces (12 in number) are named with two uppercase letters, just like their counterparts on the 3×3×3.
Surrounding each true center on each face are eight more center pieces. The four immediately adjacent to an edge are named with a lowercase subscript, e.g. Ur for the piece that is between U and UR. The four that are closer to the corners are named with two-letter lowercase subscript, like Urf for the piece that is halfway along the diagonal from U to URF.
On either side of a central edge piece are two more edge pieces with the same two colors. These are named with a single lowercase letter subscript, e.g. URf for the piece that is between UR and URF.
Moves are named as described above for the 4×4×4, only now a 5th layer exists. R1 or R is a normal turn of the outermost slice. R2 turns the next slice in, and R3, also called RS, turns the central slice. R4=L2' and R5=L'.
As before, multiple parallel slices can be combined together, for example R24 = R2R4.
Moving the entire cube can be indicated by R12345, which is abbreviated RI. (The "I" is for "identity" because such a move does not change the pattern on the cube.) This abbreviated notation allows whole-cube moves to be included in algorithms that are not specific to a particular size of cube.
The 3×3×3 can be emulated either by using moves from the set [R, L, F, B, U, D] or from [R12, L12, F12, B12, U12, D12]. The latter can also be thought of as a "dirty" emulation of the 2×2×2; it is "dirty" because you have to ignore all the center-slice pieces.
2002: 5th period of work
Although I made a note of having picked up the Cube again in 2002, I did not record any other details.
. . . Forward to page 2 . . . Last page (page 6)
This page was written in the "embarrassingly readable" markup language RHTF, and some sections were last updated on 2023 Oct 22.
 s.27
s.27