Power MANDELZOOM
Robert P. Munafo, 2023 Jul 1.
Power MANDELZOOM is a PowerPC Macintosh program for viewing the Mandelbrot Set.
History
Power MANDELZOOM began as a PowerPC port of Color MANDELZOOM.
With Apple's introduction of PowerPC Macintosh models, I added superscalar optimized iteration routines, which delivered more than 1.5 floating-point operations per clock cycle. Combined with the same adjacency optimizations and user-interface features of its predecessors, Power MANDELZOOM was the fastest and most efficient way to explore the Mandelbrot set on any Macintosh until the advent of XaoS.
The highest-precision hardware floating-point on PowerPC is IEEE binary64, with a 52-bit mantissa fraction. This was less than the 64-bit fraction given by the 68040's extended-precision floating point, and so Power MANDELZOOM's extended-precision was less: about 100 bits (30 decimal digits). To address this, in 2002 precision I implemented a "triple-double" format giving 150 bits (45 decimal digits) of precision.
In 2007, I re-implemented all of the extended-precision algorithms for greater efficiency, and added a "quad-double" precision giving 215 bits (64 decimal digits) of accuracy.
Using Power MANDELZOOM
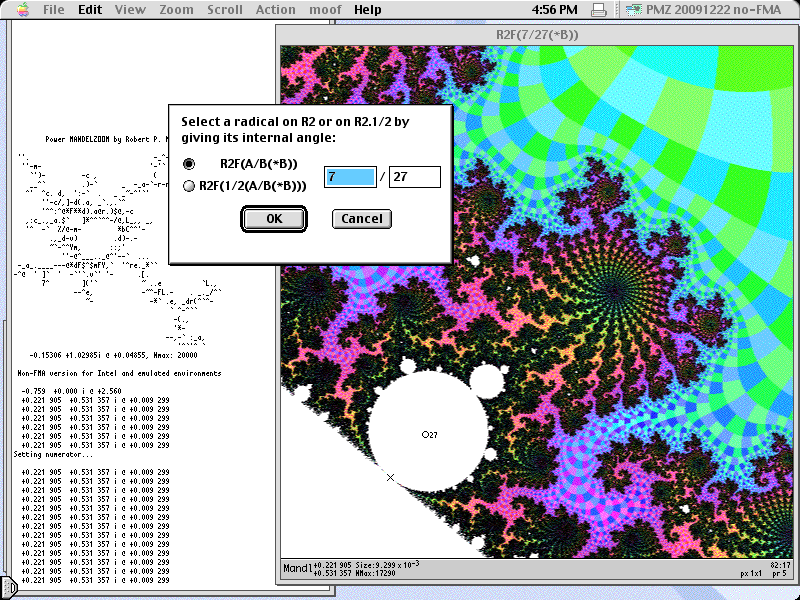
Locating a mu-unit by its internal angle
There are 5 different sets of iterator routines: 32-bit and 64-bit native floating-point, and three extended precisions using the algorithms on my F161 page. The resolution (mantissa precision) of these five modes are 24, 53, 107, 161, and 215 bits. Each is faster than the next, and the program automatically selects whichever is the lowest number of bits that will work at the current magnification level.
Power MANDELZOOM includes all of the user interface features of Super MANDELZOOM, matching the keyboard and mouse commands whenever possible. It can copy the image to the clipboard in graphic or ASCII Graphics formats, or just the coordinates. It can also produce large poster-size images and QuickTime zoom movies, rendering one chunk/frame at a time. Poster rendering can be suspended and restarted, even after an unexpected power failure.
As in Super MANDELZOOM, the image is created by a Successive Refinement algorithm with full Adjacency Optimization. The user sees a coarse image right away, then after a few seconds a somewhat finer image, then finer again after a while more, etc. Power MANDELZOOM enhances the experience in several ways:
- Pixels are divided in half on each pass: in addition to the normal 16×16, 8×8, 4×4, etc. rendering passes, there are additional passes for 16×8, 8×4, etc. This produces a smoother tradeoff between elapsed time and image quality.
- Each refinement pass begins in the center of the view and moves out towards the edges (rather than scanning from top to bottom), because the area of greatest interest is more likely to be in the center.
- The calculation precision is automatically switched when needed, and this decision is made between refinement passes. For example, the first few passes might be done in 64-bit floating point, then the remainder done in 107-bit.
When operating in the two native floating-point modes, pixels are evaluated two at a time in parallel; this gives a significant performance boost, which is possible on PowerPC because there are enough registers and pipeline bandwidth to support it. Whenever a pixel is finished, it is plotted and another iteration takes its place — so at all times there are two pixels at some stage of iteration. (See the benchmarks below)
As in Super MANDELZOOM a rectangular area can be given priority, and its pixels will be refined before the remainder of the image. In addition, the rectangular region remains selected so the refinement command can be given again more easily.

Refinement has been performed several times in the upper-left and is currently under way in the upper-right
By default Power MANDELZOOM renders the image in a rich coloring system that combines dwell, external angle, and distance estimate information in a single view. Each of these can be turned on and off to produce views that only show one or two of these. Views without dwell bands are monochrome; the program also performs dithering on lower-depth displays.
There is a greatly enhanced period detection algorithm (using the jordan curve method) that locates islands in the view even if they are far too small to see at the current magnification level.

Dithered 16-color display; showing periods and approximate locations of islands
This command creates marks in the current view which can then be used as zoom targets with more accuracy than is possible by clicking with the mouse. This makes it easy to locate the exact center of a deep embedded Julia set.
The Query function adds significantly to that of SMZ. In addition to the coordinates, period or dwell and distance estimate, Query also traces the external angle of a selected point:

Tracing an external argument
The external angle is converted to a series of fractions using the continued fraction method. In the pictured example, the final fraction 115043768/268435455 is one of the external angles leading to the cusp of the pictured island; note that the island's period is 28 and 228-1=268435455. Also, the intermediate approximation 3/7 is one of the external arguments of the cusp of R2F(1/2B1)S, which is the influencing island of the embedded Julia set surrounding this period-28 island.
Download Link
This is a disk image containing versions of Color MANDELZOOM and Power MANDELZOOM suitable for all environments from the original color Macs (under system 7) to the last PowerPC systems that had MacOS X 10.4 and its Classic environment. If you have a newer Mac (or another type of computer) and are curious, these programs also work in emulators such as BasiliskII and SheepShaver.
The URL is http://www.mrob.com/images/bin/Power-MANDELZOOM-2012.dmg or use this link:
DMG file (which contains both Power MANDELZOOM and Color MANDELZOOM)
(Right-click or Control-click the link, and "Save As..." or "Save Link As...")
Benchmarks
These benchmarks show the relative performance of the two versions of Power MANDELZOOM, running on various real Macs and emulators. (There are also benchmarks of the 68K version)
The following labels and abbreviations are used:
Versions of the program:
PPC+FMA : This refers to the standard version of Power MANDELZOOM designed to run on real PowerPC processors (not emulators), using the FMA (Multiply-accumulate operation) to improve the speed of the extended-precision calculations.
Non-FMA : This refers to the version of Power MANDELZOOM designed to be used on PowerPC emulators (like SheepShaver) running on Intel hardware; it does not use FMA operations.
Column labels:
Precision : 24 and 53 are single and double precision floating-point. 24x2 and 53x2 are special optimized loops that iterate two points in parellel (available for Dwell imaging only, not DEM/M). 107, 161 and 215 are the three extended-precision types; there is no "x2" loop for these types. 104 and 156 are earlier, far less efficient versions of 107 and 161 respectively.
Dwell : Calculating an image that shows the dwell bands, but not the filaments.
DEM : Calculating an image that shows both the dwell bands and the filaments, using the DEM/M algorithm.
ips : Iterations per second: number of times per second the calculation Z=Z2+C is being performed.
flops : number of floating-point operations per second. The ratio of ips/flops is 7 for Dwell calculation and 18 for DEM calculation.
Other abbreviations:
K, M, G : These are precisely 1000, 106 and 109.
PPC+FMA version, running on a dual 2.0 GHz PowerPC G5 970fx (a "PowerMac7,3" system from mid-2004):
prec- Dwell DEM ision ips... flops. ips... flops. 24 148 M 1.04 G 81.8 M 1.47 G 24x2 320 M 2.24 G 53 151 M 1.05 G 79.0 M 1.42 G 53x2 316 M 2.21 G 107 11.9 M 83.8 M 9.40 M 169 M 161 2.95 M 20.6 M 2.12 M 38.3 M 215 1.42 M 10.0 M 1.12 M 20.2 MNon-FMA version, running on the same 2.0 GHz PowerPC G5:
As seen by comparing to the FMA version, the use of FMA instructions
only impacts the extended-precision modes.
PPC+FMA version running on a mid-2002 iMac G4 (800-MHz PowerPC G4):
prec- Dwell DEM ision ips... flops. ips... flops. 24 45.8 M 321 M 19.1 M 345 M 24x2 123 M 863 M 53 45.2 M 316 M 19.1 M 344 M 53x2 123 M 863 M 107 4.55 M 31.8 M 2.56 M 46.1 M 161 964 K 6.74 M 770 K 13.8 M 215 496 K 3.47 M 401 K 7.22 MNon-FMA version, running under Mac OS 9 within the SheepShaver emulator, on a 2.2 GHz Intel Core i7-2720QM (Sandy Bridge, a "MacBookPro8.3" system from early 2011):
prec- --Dwell-- ---DEM--- ision ips... flops. ips... flops. 24 25.1 M 175 M 9.97 M 179 M 24x2 63.1 M 442 M 53 29.5 M 206 M 11.2 M 201 M 53x2 81.7 M 572 M 107 1.78 M 12.5 M 1.09 M 19.6 M 161 694 K 4.86 M 517 K 9.32 M 215 340 K 2.38 M 266 K 4.79 MNon-FMA version, running under Mac OS 9 within the SheepShaver emulator, on a 2.33 GHz Intel Core 2 Duo T7600 (a "MacBookPro2,1" system from late 2006):
prec- Dwell DEM ision ips... flops. ips... flops. 24 20.7 M 145 M 7.00 M 126 M 24x2 31.4 M 220 M 53 24.5 M 171 M 7.56 M 136 M 53x2 47.1 M 329 M 107 1.41 M 9.87 M 909 K 16.3 M 161 522 K 3.65 M 392 K 7.05 M 215 236 K 1.65 M 189 K 3.41 MNon-FMA version, running under Mac OS 9 within the SheepShaver emulator, on a Dual 2.26 GHz Intel Xeon E5520 (8-core "Nehalem" early 2009 Mac Pro, a "MacPro4,1" system):
prec- Dwell DEM ision ips... flops. ips... flops. 24 18.4 M 129 M 5.50 M 99.1 M 24x2 42.0 M 294 M 53 21.3 M 149 M 6.05 M 109 M 53x2 55.4 M 388 M 107 1.28 M 9.01 M 796 K 14.3 M 161 470 K 3.29 M 354 K 6.37 M 215 236 K 1.65 M 180 K 3.24 MAn early PPC version (May 3 2002) running on a 233-MHz PowerPC "beige
Power Mac G3" from late 1997:
Compare these figures to the
SheepShaver on Core 2 Duo above, and note in particular the 24x2
and 53x2 lines. In 24-bit precision this native G3-233 outperforms
the emulator; in 53-bit precision the emulator outperforms the native
machine. (The 107/161 figures do not compare directly to the 104/156
figures because the latter were an earlier and much less efficient
implementation of extended precision.)
An early PPC version (May 1 2002) running on an 80-MHz PowerPC 601 (comparable to the 1995 Power Mac 7100):
prec- Dwell DEM ision ips... flops. ips... flops. 24 1.43 M 25.7 M 24x2 15.5 M 109 M 53 1.29 M 23.1 M 53x2 9.56 M 66.9 M 104 15.7 K 110 K 6.23 K 112 K 156 9.67 K 67.7 K 3.85 K 69.3 KArtistic Bugs
I implemented many new algorithms and features during the Power MANDELZOOM period, and as such I have many images resulting from errors or bugs.

Sierpinski in the Mandelbrot set?!? |
Developing the double-double maths |
See more of my Mac software.
revisions: 20100912 original; 20100917 added benchmarks and download link; 20100918 updated disk image, add a few Wikipedia links; 20100921 added history section; 20101101 added external angle description; 20110809 added Core i7-2720QM benchmark; 20120313 add CMZ picture and expand history; 20120314 CMZ content moved to its own article; 20230701 add "artistic bug" images
From the Mandelbrot Set Glossary and Encyclopedia, by Robert Munafo, (c) 1987-2024.
Mu-ency main page — index — recent changes — DEMZ
This page was written in the "embarrassingly readable" markup language RHTF, and was last updated on 2023 Jul 01.
 s.27
s.27