Mu Atom Sizes

Robert P. Munafo, 2012 Apr 16.

As described in the entry on secondary continental mu-atoms, there is a relation between sizes of mu-atoms and their period. This relation applies to all secondary mu-atoms (those directly attached to a cardioid) and can be generalized to:

radius ≅ P sin(2π N / M) / M² for children of cardioids

where N/M is the internal angle of the child and P is the size of the parent, measured (roughly) from its cusp to the bond point with its .1/2 child.

For tertiary and all higher-order mu-atoms (that is, any mu-atoms whose parent is "circular") the formula is simpler:

radius ≅ P / M²

where P is the radius of the parent.

Examples

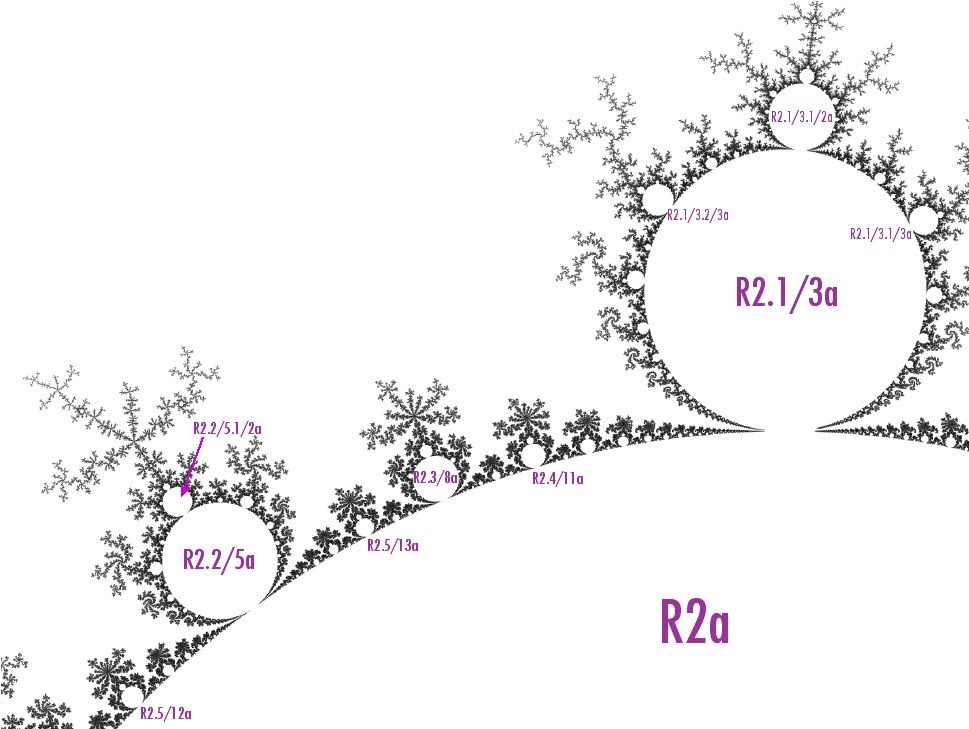
various continental mu-atoms

In this figure are several secondary continental mu-atoms, the ones that have just a single rational fraction in their R2-names. For these mu-atoms the parent is R2a, and the value of P is the distance from the elephant valley cusp R2.C(0) to the seahorse valley cusp R2.C(1/2), which is 1/4 - -3/4 = 1.0.

The largest of these is R2.1/3a. Applying the first formula above to it, we get:

radius ≅ P sin(2π/3) / 3² ≅ 0.866../9 ≅ 0.0962

which means that the "diameter" of R2.1/3a would be about twice this, or about 0.192. Actual measurements are around 0.189.

Now to compute the radius of a tertiary mu-atom, take R2.1/3.1/3a as an example. Using 0.0962 as the value of P in the second formula above, and 3 for M (because that is the denominator of the fraction 1/3), we get

radius ≅ 0.0962 / 3² ≅ 0.01069...

or a "diameter" of 0.0214. Actual measurements of the "diameter" of R2.1/3.1/3a are around 0.0193. Using the same formula the "diameter" of R2.1/3.2/3a should be the same, but measurements of it are larger: around 0.0212. That's because the distortion of the mu-unit R2.1/3 (see the mu-unit article) makes R2.1/3.2/3a be a little larger than R2.1/3.1/3a. You might be able to just barely see this difference in the figure above.

There is also a general relationship between mu-atom sizes and periods. If you compare the sizes of R2.1/3.1/3a and R2.1/3.2/3a (both of which have a period of 9) to the nearby secondary mu-atoms, you can see that both are a bit smaller than R2.3/8a (which has period 8) and a bit bigger than R2.4/11a (which has period 11).

revisions: 20030927 oldest on record; 20120416 add illustrated examples

Mu-ency main page — index — recent changes — DEMZ

This page was written in the "embarrassingly readable" markup language RHTF, and was last updated on 2012 May 14.

s.27