Notable Properties of Specific Numbers
First page . . . Back to page 16 . . . Forward to page 18 . . . Last page (page 25)
This is 86400 × 134774, the difference (in seconds) between the Windows NT epoch and the UNIX epoch. Windows NT measures time in units of 100 nanoseconds since January 1, 1601 (using the Gregorian calendar, which began in 1582) and UNIX measures time in seconds since January 1, 1970. The number of days between the two epochs is 365×(1970-1601)+89 = 134774. There were 89 leap years (because (1972-1604)/4 = 92, and 1700, 1800 and 1900 were not leap years) and the Windows NT definition uses the Gregorian calendar throughout the epoch (unlike e.g. the British Empire, which was still using Julian until 1752), so there is no subtraction of 10 or 11 days to account for any calendar change.
To convert a numeric UNIX date to the equivalent Window NT value you add 134774×86400 = 11644473600, and multiply by 107. If you allow negative numbers you can convert both ways for dates prior to the UNIX epoch (and use the proleptic Gregorian calendar if applicable).
I have also seen these "Epoch 1601" dates appear in units of 106 per second (i.e. microseconds), for example 12977910000000000 for 20120403.03:00:00.
See also 49.710269..., 978307200, 3061152000, and 2147483647.
This number's appearance in a 9th-century document from India helps prove that our place-value number system originated there. The description reads "ekâdishadantâni kramena hînâni", translated "beginning with one [which then grows] until it reaches six then decreases in reverse order". We know that the number being described is 12345654321 because it follows a description of the calculation of 111111×111111.
See also 1.234321.
13750000000 ± 11000000 = 13.75(11)×109
(age of the visible universe in years)
Current estimate of the age of the universe in years. This number comes out of calculations from data gathered by the WMAP mission, which observed the cosmic background radiation very accurately. It also assumes the Lambda-CDM model of the universe, which is the simplest model consistent with everything that has been observed so far (as of mid 2010). This model also requires the existence of dark energy and dark matter, and several predictions of cosmic inflation including a nearly-flat universe far larger than the observable universe. If all this is true, then the figure (13.75 billion years) is known to be accurate to within 0.8 percent. See also 4.6×1010, 1040 and 8.03×1060.
14182439040 = 27×34×5×7×112×17×19, and is the smallest 5-perfect number: Its divisors add up to exactly 5 times the number itself. See also 30240 and 154345556085770649600.
18426689288 is a taxicab number because 25143+13643 = 24983 + 14163 = 18426689288. Also, 18426689289 is 26413 + 1823. This is the smallest case of a taxicab number that is one less than another sum of two cubes. (from Giovanni Resta) See also 854.
The number of positions that can be reached on an ordinary 3×3×3
Rubik's Cube using any type of turns on the left and right faces, but
only 180o turns of the other four faces. In group theory terms, the
order of the
The Thistlethwaite cube-solving algorithm from 1981 [151] solves Rubik's cube by first manipulating it into a position that is an element of the 21119142223872000-member group, thence to one of the positions in this group; it then restricts all subsequent moves so that the position remains within this group, whilst reducing it to the 663552-element subgroup. See also 43252003274489856000.
The number of days in the Mayan/mesoamerican alautun, which according to Sloane's sequence A081244 is "probably the longest named period in any calendar". The other Mayan names for periods of days are:
|
See also 550420, 1872000 and 10331233010526315789473684112000.
23295638016 = 28563 ≈ 2.329×1010
This is the smallest cube that can be expressed as a sum of a sequence of consecutive cubes in more than one way: 28563 = 2133 + 2143 + ... + 5553 = 2733 + 2743 + ... + 5603. See also 216 and 8000.
This is the length of the day in paramanus, a small unit of time in Hindu mythology. There are many different Hindu time systems that contradict each other; this is one of the more irregular ones.
|
See also 405000, 4665600000000.
This number is polydivisible, meaning that for any N, its first N digits are divisible by N: 3 is divisible by 1, 36 is divisible by 2, 300 is divisible by 3, and so on. 30000600003 is also a palindrome, and it is the largest number with both properties.
See also 381654729 and 3608528850368400786036725.
46000000000 = 4.6×1010 = 46 billion
(radius of the visible universe in light-years)
The radius of the visible universe in light years, assuming the Lambda-CDM model ("standard cosmological model") with parameters that most closely explain the spatial frequency distribution of the cosmic microwave background radiation. This size is 4.45×1026 meters and 2.75×1061 in Planck units.
This is a "comoving distance", a cosmological term which roughly describes a distance one would get if it were possible to measure "instantly" without the effects of relativity. The matter that produced the cosmic background radiation, emitted 13.72 billion years ago, has subsequently traveled away from us (while forming into galaxies) and is now about 47 billion light years from us.
There seems to be a paradox: this is over three times as big as the age of the universe would suggest. Moving at the speed of light, such matter could only have gotten as far as 13.72 billion light years in any direction. The paradox is resolved by the fact that much of the time was spent traveling across a smaller universe; and much of the "extra travel distance" added by the universe's expansion has already been covered by the photons during the younger, smaller universe. So the space can be expanding faster than light (relativity does not limit how fast the space can expand, only the speed at which things inside the space can travel).
I have a long description with "pictures" in plain ASCII graphics like this:
0 sec * 0 cm 1 sec U::;a::;B 2 cm 2 sec U-:-:-:-a-:-:-B-b 4 cm 3 sec U--:--:--:--a--:B-:--:--b 6 cm 4 sec U---:---:---:---B---:---:---:---b 8 cm 5 sec U----:----:----B----a----:----:----:----b 10 cm 6 sec U-----:-----:-B---:-----a-----:-----:-----:-----b 12 cm 7 sec U------:----B-:------:------a------:------:------:------b 14 cm 8 sec U-------:-B-----:-------:-------a-------:-------:-------:-------b 16 cm 9 sec U------B-:--------:--------:--------a--------:--------:--------... 18 cm 10 sec U--B------:---------:---------:---------a---------:---------:--... 20 cm 10.8 s B----------:----------:---------:----------a----------:--------... 21.6 cmRead it for a full explanation of what is called a "nearly empty universe" model.
In reality, due to effects of gravity, energy, dark matter, and dark energy, we would never see all the way to the edge of an infinite space (whether flat Euclidean, or negatively curved hyperbolic). In a critical density model (where there is neither unending expansion nor a reversal to a "big crunch")t the distance we could "see" would be exactly three times as far as the "age" of the universe: 3×13.72 = 41.16 billion light years. In fact, the density is not exactly critical, so the current size of the visible universe is a little bigger, about 47 billion light years.
For a lot more on this, and more accurate diagrams, see Wright's cosmology FAQ [213] as well as the articles by Davis and Lineweaver [190], [194].
See also 4.6×1010, 4.339(35)×1017, 3×1023, 4.45×1026, 1040, 8.03×1060, 1063, 1.1×1089, 1097, 10110, 8.72×10184, 1.75×10245, 1.41×10408, 10500, and 1022650000000.
The largest known triperfect number
61917364224 = 1445 ≈ 6.191×1010
This is the smallest 5th power that is also the sum of four distinct 5th powers: 1445 = 275+845+1105+1335. All bigger solutions up at least as high as 24485 are just multiples of this one. Because 144 is a square, this also happens to be the smallest 10th power that is the sum of four distinct 5th powers. There are plenty of other numbers that set "smallest sum of powers" records; for a long time, searching for such sums was very popular because of their similarity to the Fermat's Last Theorem problem.
What's particularly interesting about this number is the serendipitous way in which it was discovered. In 1966, two mathematicians programmed a computer to find solutions involving a sum of five 5th powers. They had no idea that there might be a solution with only four 5th powers, and in fact Euler had conjectured that there were none. But, due to an error in programming, the computer treated 0 as a valid number, and one of the solutions they found included 05 as one of the five 5th powers. As a result, they were pleasantly surprised to find that they had disproven a conjecture of Euler purely by accident!
Number of particles (protons, neutrons, and electrons) in a bacterium, based on the figure 10-12 for the mass of a bacterium1. See also 713580, 1014 and 5.1843×1022652507173.
An estimate of the total number of people that have ever been born (assuming Darwin and evolution). The number depends highly on the decision on when pre-human apes begin to count as "people". This estimate draws the line at about 55000 BC. See this page for an explanation of the formulas used to compute the number. See also 6771000000, 5×1030, and 117000000000.
100000000000 = 100 billion = 1011
This number is the na-yu-ta (なゆた) of the Lotus Sutra as it appears in e.g. Tendai schools of Japanese Buddhism. In that context it is the "12th of sixty digits" counting from the least significant: the digits are 1's, 10's, 100's, etc. up to the 60th being 1059. The name is descended from the Sanskrit niyuta as used in e.g. the Lalitavistara sutra, but is sometimes used to mean other numbers such as 106. The Hindi name for 1011 is kharab. There are many other powers of 10 that have special names in Sanskrit; see also 1059.
1011 is one of the largest numbers explicitly named in a published music lyric. It is heard in Message in a Bottle by The Police, which has the lines "100 billion bottles / washed up on the shore". Sting is from England, but the song was written well after 1974 when they switched to the short scale, so I am assuming he was referencing billion=109 when writing this lyric. See also 525600, 8675309, 1012, 1027 and 101010.
Earlier (pre-1939) military Enigma machines used only 6 patch cords in the plugboard (see 150738274937250 for a description), providing this many ways to choose letters to swap.
An estimate of the total number of people who have ever lived, used by Tony Padilla in this incorrect answer to two different but similar stated problems about a "number that [no] human has thought of".
See also 96000000000
(the astronomical unit in meters)
An astronomical unit (AU) in meters, which is approximately the distance from the Earth to the Sun. It is a common unit of measurement in astronomy; for example, the distances of extrasolar planets from their parent stars are usually given in AU.
For quite some time an "astronomical unit" was defined as the radius of a circular orbit in which an unperturbed particle of infinitesimal mass would orbit the Sun in one Gaussian year. This is not quite the same as the Earth's semi-major axis mainly because the Gaussian year, computed in 1809, was not entirely accurate and the physical world (in this case, mainly the solar mass) is subject to continual change; see sidereal year. By Gauss' calculations, the AU was this many metres long.
Due to its dependence on constants, this definition of AU ignores any actual changes in the Earth's orbit or the accuracy of our measurements thereof. However, it remains dependent on the solar mass and the gravitational constant (or their product which is known more accurately than either of the other two). In 2012, a definition not depending on these, 149597870700 was adopted by the IAU.
Attempts to actually measure the physical size of Earth's orbit have a long history. Classical Greek and Chinese estimates (Aristarchus of Samos, Eratosthenes, Hipparchus, the Zhou Bi Suan Jing and Ptolemy) were based on observations that were subject to measurement errors that made an accurate determination of the true value impossible. Godefroy Wendelin repeated the technique of Aristarchus around 1630 and attained a better value but the magnitude of the error was still at least as large as the value itself. Christiaan Huygens made an estimate based on the notion that Venus and Mars are of similar size to the Earth (but would have had no way of knowing this to be true).
The number was first calculated in a reliable way by Jean Richer and Cassini, who determined the parallax of Mars at opposition in 1672, arriving at an estimate of 21700 Earth radii or 1.38×1011 meters. This estimate stood for about 100 years until 1771, when Jerome Lalande compiled the data from numerous observations of the transit of Venus to get an estimate of 1.53×1011 meters.
Other, better estimates were possible beginning in the late 1800's when accurate non-astronomical methods were used to measure the speed of light. These could be compared to known figures for light travel time from Jupiter (attained by observing eclipses of its moons). In 1900-1901 and again in 1930-1931, parallax observations of asteroid 433 Eros enabled even more accurate measurements of the size of the solar system, giving the best estimate of the astronomical unit until the early 1960s, when radar allowed a direct measurement of the light travel time to Venus and Mars.
See also 8.794143, 149597870700, 5878625373183.6 and 9.46×1015.
As of 2012 Aug 31, by a resolution of the International Astronomical Union (IAU), the official definition of the astronomical unit is this many meters. The current "actual" value is probably closer to 149597870691.
This is 1/4 of 635013559600. If you are dealt 13 cards purely at random out of a standard 4-suit, 52-card deck, the odds of getting all 13 cards of a suit are 1 in 158753389900. See also 2.235197...×1027 and 8.065817...×1067.
The word "SECRET" encoded into numbers using the simple code A=01, B=02, C=03, etc. For examples of encoding words using equations, see my RIES page. See also 13051919010705.
293318625600 is a divisibility record-setter, also called "highly composite". Its factorisation is 26×34×52×72×11×13×17×19 and it has 5040 divisors. Ramanujan studied highly composite numbers, and in 1915 published a substantial list of them — but notably left this one out (the list goes up to 6746328388800 which is about 22× bigger; this is discussed in the Numberphile video "Infinite Anti-Primes").
293318625600 has 5040 divisors, 5040 itself has 60 divisors, 60 has 12 divisors, 12 has 6 divisors, and 6 has 4 divisors — together these make up a chain with 6 distinct values, all highly composite. This is the longest such sequence given the requirement that all members of the chain are divisibility record-setters. 4 has 3 divisors but 3 is not highly composite; extending the chain in the other direction gives (6.700591...×1074 which also is not highly composite). There are only a couple larger numbers that are a part of any such "chain" (and 195643523275200 is the largest). (Originally noticed by Raphie Frank98)
Approximate pressure in the centre of the earth, in Pascals (kg/m-s2).
See 3.1418708596056 and 137.035.
Five hundred billion, the largest value I have seen on paper currency: the 500000000000 Dinar note which was issued in Yugoslavia as part of the 1993 series during their civil war and hyper inflation. Here is an image. This hyperinflation was much worse than the German 1923 episode but not as bad as Hungary's experience during World War II. However, the Yugoslavs probably have the record for the largest number on a piece of currency (the Hungarian "100 million B-pengo" represents 1 000 000 000 000 000 000 000 = 1021 Pengo, but the number on the note was "egy-milliard", 1 000 000 000, because the currency had been reissued in units of "B-Pengo" with one B-Pengo equal to 1012 of the older Pengos. If you want to call it the highest-denomination note, then you'd also have to count the Yugoslav 1994 10000000 Dinar note which is equivalent to 1027 pre-1990 Dinars). The Yugoslav currency was re-issued four times, in 1990, 1992, fall 1993 and January 1994, with multiplier factors of 10000, 10, 106 and 109 respectively, thus the 1994 Dinar was worth 100000000000000000000 (1020) pre-1990 Dinars. (For more about record-setting currency, visit this site.)
The number of distinct ways to make a map of the 48 contiguous states of the United States, using 4 colours, such that no two states that share a border are of the same colour, and where the 4!=24 different ways of reassigning the colours do not count as distinct. See 25623183458304 for a full description.
The number of 13-card "hands" selected from a 52-card deck. This is 52!/(39!×13!). To understand the formula, imagine that you first shuffle the cards (52 factorial), then you take the first 13 to make a hand, but it doesn't matter what the order of those 13 is (divide by 13!) nor does it matter what the order of the other 39 cards is (divide by 39!).
See also 158753389900, 2.235197...×1027 and 8.065817...×1067.
Length of Earth's orbit in metres, based on this definition of the astronomical unit.
See also 584058562.475.
(the short-scale trillion)
A trillion in the "short scale" system used in most of the English-speaking world. In the original Chuquet system, a "trillion" was 1018.
This is (as far as I am aware) the largest number explicitly named in any published music lyric. It is heard in Unacceptable by Bad Religion, which talks about chemical pollution, contains the lines "It's one part per trillion... unacceptable / One part per billion... unacceptable / One part per million... unacceptable". There are also indirect references (see 101010) and strings of digits not intended as numbers (see 0118 999 881 999 119 725 3).
The number of distinct ways to make a map of the 48 contiguous states of the United States plus the District of Columbia, using 4 colours, such that no two states that share a border are of the same colour, and where the 4!=24 different ways of reassigning the colours do not count as distinct. See 25623183458304 for a full description.
This is the 61st Fibonacci numbers, and the first one containing each of the digits 0 through 9. See also 1026753849 and 295147905179352825856.
3546146300288 = 27×27704267971
This is the number of possible solution patterns to Sudoku puzzles, if you ignore differences that amount merely to a "relabeling" (like changing all 3s to 7s and vice-versa). See also 362880, 6670903752021072936960, 5524751496156892842531225600.
This is the length of the day in thruti, a small unit of time in Hindu mythology. There are many different Hindu time systems that contradict each other; this one is notable for involving a fairly orderly set of powers of 60, and also seems to involve the largest total ratio between smallest and largest unit.
|
The system can be extended, as I have shown, to longer periods of time. The 60-day ritu is one sixth of the solar year (so is actually closer to 61 days); the seasons are vasant (spring), grishma (summer), varsha (monsoon), sharad (autumn), hemant (dewey), and shishir (winter) 19. There is another Hindu time division system that divides the day into powers of 30. See also 405000, 26244000000.
The number of miles in a light year, both of which are defined precisely making this number exactly 9460730472580800/1609.344.
See also 149597870691, 3.08568025×1016 and 5.8535×1050.
6746328388800 = 26×34×52×72×11×13×17×19×23
The largest highly composite number in a list that Ramanujan published in 1915. See also 293318625600.
This is 327, which can also be expressed 333, 3④3 or 3⑤2. The latter two forms use the hyper4 and hyper5 operators.
The number of ways to pay $1.00 in coins, if the denominations are 1, 5, 10, 25, 50, and 100, and if different orderings are counted as different ways of paying (for example, 25+50+10+10+5 is different from 5+10+50+10+25). (From Andrew Neitsch, related to the problem 1.3333398333445...×1031; see also 293).
A light year in kilometers.
The number of distinct ways to make a map of the 48 contiguous states of the United States, using 4 colours, such that no two states that share a border are of the same colour. See 25623183458304 for a full description.
The word "MESSAGE" encoded into numbers using the simple code A=01, B=02, C=03, etc. For examples of encoding words using equations, see my RIES page. See also 190503180520.
This number's digits are the same as those of its prime factorisation when expressed in the usual way: 13×532×3853×96179 = 13532385396179. It is the first known counterexample to J.H. Conway's "Climb to a Prime" conjecture (one of Conway's so-called $1000 problems), and was found by James Davis in 2017.
Davis conjectured a counterexample in the form of a number that maps onto itself; in particular, one whose largest prime factor is to the 1st power, meaning that the number's final digits are the same as this largest factor (96179 in this case). That means that the number has to be of the form (m×10y+1)×p where p is that largest prime factor (in this case, m=1407, y=5, and we have 1407×105+1 = 140700001 and 140700001×96179 = 13532385396179.) Expressing n in the form (m×10y+1)×p made it a lot quicker to search for a satisfactory m and p and thereby find an n for Davis' conjecture and thus the counterexample for Conway's.
Numberphile discuss this in their video named (appropriately, though perhaps not creatively) "13532385396179".
See also 225, 2592, and 35149.
The extraterrestrial population of the Solar System according to Thomas Dick in his 1837 work Celestial Scenery; or, The Wonders of the Planetary System Displayed; Illustrating the Perfection of the Deity and a Plurality of Worlds. Performing a calculation similar to that of Christiaan Huygens, he estimated the surface area of all the known bodies in the solar system (including even the rings of Saturn), multiplied by the population density of England at the time (280 per square mile) and concluded that there would be roughly 2.19×1013 extraterrestrial beings. The gas giants accounted for over 99% of the total, and only Vesta was given a population less than that of Earth.
See also 6.0573×1022.
The number of distinct ways to make a map of the 48 contiguous states of the United States plus the District of Columbia, using 4 colours, such that no two states that share a border are of the same colour. States that meet only at a single point (Utah and New Mexico, and Arizona and Colorado; see Four Corners) are not considered to "share a border". The answer, and a description of algorithms used to calculate it, are in Knuth [169] section 7.1.4 (Binary Decision Diagrams), (p. 233 in the 2011 edition). Without DC the number is 12811591729152.
See also 68656026, 533816322048, and 1067632644096.
The CATENATIVE DOOMSDAY DICE CASCADER rolls a 1!!!
(gross world product in dollars, 2008)
An estimate of the 2008 Gross world product, in 2000 US dollars, based on the following estimates: the value for the year 2000 of $4.1×1013 in 2000 US Dollars (from the Wikipedia page), an annual growth rate of 3.56% (based on the average of five consecutive estimated growth rates for 2005-2009 from the same Wikipedia page). Another more current estimate comes from the per-capita figure of $10,500 (from the same Wikipedia page) times the world population, giving $7.1×1013 in 2008 dollars. See also 2.315×1016
(cells in a human body)
(bacteria living in and on a human body)
Estimates of the number of cells in a typical human's body range from 1013 to 1014.
1014 is also an estimate of the number of bacteria living on or in a human body.2 Another source123 gives the value 6.5×1013. Most of these are either in the skin or somewhere inside the digestive tract (mouth, intestine etc.) and provide essential support to digestion and other vital functions. See also 6771000000, 75250000000, 1019 and 5×1030.
1014 is also an estimate of the computing rate (in floating-point operations per second) needed to simulate a human brain. See 1019.
150738274937250 = 26!/(6!×10!×210)
The various Enigma machines used during World War II had the ability to swap pairs of letters during the encryption process, and the pairs of letters to swap were selected by connecting pairs of electrical terminals with patch cords. There were 10 cords allowing 10 pairs of letters to be chosen, and 26 terminals. For p pairs of letters there are 26!/((26-2p)!×p!×2p) possible configurations. p=6 gives 100391791500, and p=10 gives this number 150738274937250. See also 105456, 1.59×1020, and 9.26×1022.
195643523275200 = 26×34×52×72×11×13×17×19×23×29
This is the largest highly composite number for which the number of divisors (in this case, 20160=26×32×5×7) is itself a highly composite number. The number of divisors of 20160 is 84, which is not highly composite. See also 5040, 293318625600, 8.976124...×1017, and 6.700591...×1074.
This is 8! / 4! = 1!×2!×3! × 5!×6!×7!×8!, and it is a perfect square: 145152002 = 210691031040000. We can see why it is a perfect square by considering the product of all eight factorials, with 4! included:
1! x 2! x 3! x 4! x 5! x 6! x 7! x 8! = 1 x 1 x 2 x 1 x 2 x 3 x 1 x 2 x 3 x 4 x 1 x 2 x 3 x 4 x 5 x 1 x 2 x 3 x 4 x 5 x 6 x 1 x 2 x 3 x 4 x 5 x 6 x 7 x 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8This product cannot possibly be a square, because there are six 3's in one column and three 6's, meaning that it is a multiple of 39. Other similar problems result from it having columns of odd height. But if we remove all the even numbers from the main diagonal:
1! x 2! x 3! x 4! x 5! x 6! x 7! x 8! / 8!! = 1 x 1 x 1 x 2 x 3 x 1 x 2 x 3 x 1 x 2 x 3 x 4 x 5 x 1 x 2 x 3 x 4 x 5 x 1 x 2 x 3 x 4 x 5 x 6 x 7 x 1 x 2 x 3 x 4 x 5 x 6 x 7now all columns are of even height, so the product is a square. The numbers that got removed are 8!×6!×4!×2!, which is 8!! (the "double factorial" of 8), and 8!! = 4!×24. Since 24 is a square, we multiply that back in, and see that (1!×2!×3!×4×5!×6!×7!×8!)/8!!)×24 = 1!×2!×3!×5!×6!×7!×8! is a perfect square.
The same holds for any similar product of factorials from 1! to N! where N is a multiple of 4. For a bigger example, see 2.703176857×106940.
The smallest number with a persistence of 11: 2×7×7×7×7×7×7×8×8×8×8×8×8×9×9 = 4996238671872, 4×9×9×6×2×3×8×6×7×1×8×7×2 = 438939648, 4×3×8×9×3×9×6×4×8 = 4478976, 4×4×7×8×9×7×6 = 338688, 3×3×8×6×8×8 = 27648, 2×7×6×4×8 = 2688, 2×6×8×8 = 768, 7×6×8 = 336, 3×3×6 = 54, 5×4 = 20, and 2×0 = 0. As of 2011 it is still unknown whether there is a number with a higher persistence, although it has been proven that there are none less than about 10333 [219].
See also 679 and 77777733332222222222222222222.
This is 248, or 4 to the power of 4! (see also 729).
It is the number of Ethernet MAC addresses (normally expressed at 12 hexadecimal digits), which is enough for thousands of unique numbers for everyone on Earth. Nevertheless, the standards organisation responsible for this detail of the Internet requires that manufacturers use 90% of the numbers allocated to them, and has only planned for "a target lifetime of 100 years" (probably dated from around 2001, the year of the IEEE 802-2001 standard, which notes that "The requirement for the use of 64-bit addresses in new applications is under consideration"). See also 4294967296.
3.1104×1014 = 360×100×2000×(4+3+2+1)×43200
(lifetime of Brahma)
The lifetime of Brahma in Hindu mythology (see Hindu calendar), see 622080000000000 for more details.
This is the product of two primes, 3536123 × 128541727, and also the sum of these two plus all the primes in between: 3536123 + 3536129 + 3536131 + ... + 128541719 + 128541727. Thus it has the "39 property"; it is the 5th number with this property after 10, 39, 155 and 371.
There is also a reasonably good chance that it is the largest, but it's hard to tell. As N gets larger, the odds of this property happening fall off quite quickly. If there is another, it is greater than 3.63 × 1018.
This is an example of a phenomenon that is a counterpart to Guy's Strong Law of Small Numbers (see 91), and unfortunately not called the "Strong Law of Large Numbers" (which is an unrelated and much more formal law of statistics).
If two properties are unrelated, and if the likelihood of occurrence of both properties for any one integer N falls "quickly enough" then the set of such numbers is probably small and finite. (If it were not small and finite, there would be a relation between the two properties.)
Without being rigorous and getting into heavy number theory, you can often make a pretty good guess as to whether a set of numbers is finite or not by a brute-force search. If the numbers found by the brute-force search suggest a probability of less than 1/N for any given integer being in the set, then the set is probably finite. If the probability is 1/N or more, the set is probably infinite.
To give a simple example: consider a hypothetical "search" for powers of 2. The odds of any integer N being a power of 2 can be stated as log2(N)/N, because there are log2(N) powers of 2 spread out over the first N integers. log2(N)/N is bigger than 1/N, so that implies that there are an infinite number of powers of 2. A computer search would "verify" this by showing that for the first N integers there are approximately log2(N) powers of 2.
When the set of numbers is even more rarely distributed, the method isn't really useful. For example, consider integers of the form 22n. For each N the probability is log2(log2(N))/N, only slightly more than 1/N. The numbers are so spread out that a brute-force search doesn't give enough data to make a clear decision. It could spend less than a second finding the first 5, and years before finding the 6th. This is why we can't be too certain that 454539357304421 is the highest number with the "39 property".
An example of a set of numbers that is right "on the edge" of decidability by this method is the Mersenne primes. These are primes (probability roughly 1/ln(N)) that are 1 less than a prime power of 2 (probability log2(N) ln(log2(N))/N). The combined probability is ln(2) ln(log2(N))/N, or ≈ 5 ln(2) ln(log2(N))/N if you account for the fact that Mersenne numbers are known to be relatively prime to all smaller Mersenne numbers. These odds fall only a tiny bit less fast than 1/N — too close to call from a brute-force search alone. In fact, the formula K ln(2) ln(log2(N))/N agrees very closely with the number of known Mersenne primes, although K is somewhat less than 5. The search for more Mersenne primes is ongoing, and much research has yielded neither proof nor disproof that they are infinite in number.
According the Wikipedia, this is the surface area of the Earth in square metres. If the Earth were a perfect sphere with a circumference of 40,000 km (as was intended in the original definition of the metre) this number would be 16×1014/π, about 5.093×1014.
588522607645608 ≈ 5.885226...×1014
This is one in a series of near-misses to Fermat's last theorem discovered by Ramanujan, of which 1729 is the famous first example. In this case we have: 656013 + 674023 = 838023 + 1. This, together with 1729 itself, 1030301000 and 336365328016955757248 are all generated by the same formulae. See this article for details.
See also 635318657.
622080000000000 = 2×100×360×2×1000×4320000
The length of the cycle of existence in Hindu mythology. After each mahayuga (a period of four ages lasting 4320000 years, see 432000) there is a period of another mahayuga during which the world is undifferentiated. 1000 mahayuga make up the kalpa or manvantara, 4320000000 years, called a "day of Brahma", 1 day in the life of the god Brahma. After such a period Brahma sleeps for another equal period, so the day and night of Brahma last 8640000000 years. 360 such day-night periods is the year of Brahma, 3110400000000 of our years (360 × 8640000000). 100 such years is the maha-kalpa, the lifetime of Brahma, 311040000000000 normal years. At this point everything including Brahma ceases to exist for an equal period, then the cycle repeats over and over forever. The length of the whole cycle is 622080000000000=6.2208×1014 years.
A "Cunningham chain" is a sequence of prime numbers where each one is twice the previous one plus one. For example, {2, 5, 11, 23, 47} is the first chain of length 5 and {89, 179, 359, 719, 1439, 2879} is the first of length 6. Gunter Loh found the first chain of length 13, beginning with 758083947856951.
This is noted for being the first number n for which 2n/log(2) is greater than an integer but 2/(2(1/n)-1) is less than the same integer, a property more commonly expressed as an inequality with the floor() function around the 2n/log(2) and ceil() around the other part. This seemingly stunning fact is a little more understandable if we examine some values of the two expressions:
|
The values in the 2n/log(2) column always have the digits of 2/ln(2) = 2.885390081777926814719849... and as we can see 2/(2(1/n)-1) tends towards being less than that by 1. The margin of opportunity for floor(2n/log(2)) to be different from ceil(2/(2(1/n)-1)) narrows as n gets bigger, tending towards 1-ln(2)/(6n). The floor() vs. ceil() inequality will fail when 2n/log(2) is X.999999... and 2/(2(1/n)-1) is X.000000... for some X; and the "game" of finding an n such that this happens has a lower probability as n increases. Such values are listed in OEIS sequence A129935.
(the "smallest zillion")
1015 is a quadrillion in the United States. In France and under the old British system, it is called thousand billion (or sometimes billiard, no relation to the game). Colloquially people use the word zillion to refer to numbers larger than those with familiar names, that is, larger than trillion and therefore this is about the smallest "zillion". See also grillion and 1040.
The smallest (positive) integer whose name (in English) has the vowels A,E,I,O,U, plus Y, in order: "one quAdrillion EIght thOUsand (and) twentY". When answering problems like this we don't count the letters in "and" because not all people agree on when to include an "and". See also 34, 1005, 1025, and 1084.
The first of a set of 1131 consecutive composite numbers: Every number from 1693182318746372 through 1693182318747502 is composite. This is the first time there are 1000 or more composite numbers in a row. See also 370262.
3014170389176410 ≈ 3.01417×1015
The amount (in US dollars) demanded in a lawsuit filed in 2007 by a Katrina victim in Louisiana against the U.S. Army Corps of Engineers. This set a record, which was surpassed in 2009. See also 2×1036.
The value of the Earth, in U.S. dollars, based on the exoplanet value formula developed by Greg Laughlin of UCSC:
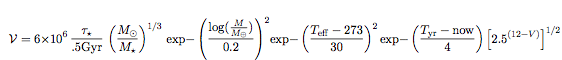
5056584744960000 ~= 5.057×1015
This is "8 superfactorial", 1!×2!×3!×4!×5!×6!×7!×8!. Remove 4! from the product and get 210691031040000, a perfect square.
The value of the Earth (in US dollars) as computed by the History Channel in 2012 October, based on the idea of selling all its component materials (iron, gold, lumber, etc.) at then-market prices. See also 5×1015 and 1.58098×1022.
9007199254740992 = 253 ≈ 9.0072×1015
This is the limit for expressing integers exactly in 64-bit IEEE double precision format. See also 9.22337×1018.
9460730472580800 = 9.4607304725808×1015
(a light year in meters)
The distance (in meters) that light travels in a year, called a light-year. As recommended by the IAU, it is based on the official (defined) speed of light, and the Julian year. Because both of those have precise definitions, the ratio (1 light year)/(1 meter) is exactly the integer shown here.
See also 31557600, 149597870691, 5878625373183.6, 3.08568025×1016 and 5.8535×1050.
According to Richard Crandall [168], the "longest calculation ever performed" to get a yes-or-no answer, is 1016 fundamental operations, to prove that the 22nd Fermat number (2222+1) is composite. They didn't even find any factors — merely a yes-or-no answer that there is a factor. Crandall says this amount of computation is equivalent to that used to produce the entire Pixar-Disney movie Toy Story.
21119142223872000 ≈ 2.1119...×1016
The number of positions that can be reached on an ordinary 3×3×3
Rubik's Cube using only 180o turns of the top and bottom faces,
plus any type of turn of the other 4 faces. In group theory terms, the
order of the
The Thistlethwaite cube-solving algorithm from 1981 [151] solves Rubik's cube by first manipulating it into a position that is an element of this group, then restricting all moves from that point on so that the rest of the moves remain within this group, whilst reducing it to the 19508428800-element subgroup. See also 663552 and 43252003274489856000.
23148855308184500.00 = 2.31488553081845×1016 ≈ 267/6375
This is the amount (in dollars) that was charged to the prepaid debit card of New Hampshire resident Joshua H. Muszynski for a pack of cigarettes purchased at a gas station. The same amount was also charged to "fewer than 13,000" other customers in July 2009 due to a Visa computer programming error[209],[210],[212],[214]. The amount, $23,148,855,308,184,500.00 (over "23 quadrillion" dollars as accurately reported by many headlines), is over 300 times the total gross world product in the year 2008. It can be expressed as 2(64+5)/255 - 3536 cents (rounding down). This interpretation is a clue to the likely programming error: 2314885530818450000 in base 2 is 0010000000100000001000000010000000100000001000000001001001010000. It had been pointed out that if interpreted as a 64-bit quantity, and taken in groups of 8, the top 6 groups of 8 are each equal to 001000002=3210, the ASCII value for a blank space. For the same reasons that 1/999 = 0.001001001..., a bit-pattern like this will occur in binary arithmetic when you take a power of two (like 269) and divide by 255=28-1.
See also 2425, 10137 and 102.96216823...×101542.
(the parsec in meters)
The length in meters of a "parsec", a unit of distance used in astronomy that is roughly 3.26 light years. This distance is equal to the radius of a circle whose circumference is 360×60×60 times the mean distance from the Earth to the Sun. See also 5878625373183.6 and 3.08568025×1022.
89875517873681764 = 2997924582 ≈ 8.987552×1016
The square of the speed of light, in m2/s2. This value is exact, by definition (see 299792458).
This is the ratio between mass and energy in the famous equation E=mc2 commonly associated with Albert Einstein. Expressed as a ratio of mass to energy, the units are in kilograms per joule, and since a joule is a kg.m/s2, the units cancel out. However, simply having the units cancel out doesn't make it a law (see 3.14187). Any velocity would work, say the speed of an electron orbiting an atom in the Rutherford-Bohr model. However, the speed of light is special and a mass-energy equivalence using c2 as the ratio is essential for consistency of physical laws.
The first evidence of this came in the 1860's, when Maxwell's equations were developed to describe the interactions between the forces of electricity and magnetism. This was the first field unification in physics, and the only one to be accomplished with classical mathematics. The equations, which predicted the existence of radio waves (and were shown to be a perfect model thereof) stipulated that charged matter interacted over a distance, mediated by a wavelike phenomenon traveling at a fixed velocity, which Maxwell identified in 1864 as being the same velocity as the speed of light. (See 299792458 for the related and earlier history of how the speed of light was measured).
Maxwell was aware of various experiments involving magnets and charged objects attracting and repelling each other. His description of the electro-magnetic waves explained all these experiments. A simple example is two objects with like charge repelling each other. Using modern notation (a Feynman diagram) an interaction between two charged particles looks like this (two electrons represented by e1, e2 exchange a photon represented by y) :
time e1 e2 : | | : | | : | .~_)\ : | .~_) \ : | .~_) \ : | ,~_) y \ : |_) \ : / \ : / \ v e1 e2
The thing to notice here is that one electron starts moving to the right before the other one starts moving to the left. In order to comply with the law of conservation of momentum, one must conclude that the electromagnetic energy has mass. The determination of how much mass it must have is fairly easy: given that it has a known speed, and given existing laws relating energy, force, acceleration, velocity, inertia and momentum, the ratio between mass and energy has to be c2 so that the center of mass remains fixed.
Physicists were not about to adopt mass-energy equivalence as a law (it was very difficult to imagine, and was not even expressed out loud until Max Abraham in 1903, see [181]), and they spent many years pursuing various luminiferous aether theories to explain how energy could be exchanged non-instantaneously without the need to also exchange mass. However, following efforts by J. J. Thomson, Oliver Heaviside, Wilhelm Wien and George Frederick Charles Searle to relate mass to electromagnetism (see the mass in special relativity article), experiments by Walter Kaufmann with electrons in vacuum tubes established that the electron gains mass in proportion to the amount of energy that has been used to accelerate it to a given velocity. Also, the Nichols radiometer experiment in 1901 showed that light does indeed impart momentum (radiation pressure).
Various early versions of mass-energy formulas during this period had terms expressing a change in mass as a ratio between energy and c2. The terms had extra factors of 2 and of 4/3 that came from incomplete understandings of electromagnetic self-energy or from the complexities added to mediate force transfer through the luminiferous aether, so the formulas contain things like "8E/3c2" or "4E/3c2".
Einstein's contribution was to explain everything in ways that completely eliminated the need for the luminiferous aether. He used thought experiments involving moving bodies that emit two bursts of light each carrying energy E/2 in opposite directions; calculations based on the doppler shift of the light, considered from two different reference frames, show that momentum is conserved only if the object's mass diminishes by E/c2.
An estimate of the number of words printed on paper during the first 500 years of the printing press (roughly 1456 to 1956). (From Straight Dope)
111007923832370565 ≈ 1.11×1017
This is the number of possible BINGO cards, of the standard type having a 5×5 grid in which each column has five numbers drawn from a set of 15, except the centre column with four numbers and a "FREE" square. Each column has its own set of 15 from which to draw its numbers (for example the 2nd column gets numbers from 16 to 30 inclusive) so we can choose numbers for a column without affecting the pool of numbers available to the other columns. Therefore each column has its own probabilities independent of the others, and the columns each have 15×14×13×12×11/(5×4×3×2)=3003 possibilities, except the centre one having 15×14×13×12/(4×3×2)=1365. Matt Parker has a video on the related BINGO Paradox. See also 2.480914...×10109.
This is 6403203 and is just about 744 less than the Ramanujan constant. It appears in the Chudnovsky series approximation of pi.
262537412640768743.9999999999992500725971981... = eπ√163 ≈ 2.625×1017
(the Ramanujan constant)
An example of a "coincidence" that isn't. The value of eπ√n is a near-integer for a few special values of n. There are twelve 9's in a row. The integer approximated by this is 262537412640768744, which is also equal to 6403203 + 744 = (26×3×5×23×29)3 + (23×3×31). The near equality can also be transformed into an approximation of π:
π ≈ ln(6403203+744) / √163
which is correct to 30 digits after the decimal point.
One constant like this is a fluke and almost believable if you look at it statistically, but it becomes more interesting when you know that there are a few other similar, smaller constants:
eπ√67=147197952743.999998662..., approximately equal to
52803 + 744 = (25×3×5×11)3 + 23×3×31
eπ√43=884736743.9997774..., approximately equal to
9603 + 744 = (26×3×5)3 + 23×3×31
eπ√19=885479.7776..., approximately equal to
963 + 744 = (25×3)3 + 23×3×31
eπ√163 is sometimes called the "Ramanujan constant", but that is not historically accurate — there is no record of Ramanujan discussing this number, although he did discuss these, which do not fit into the same pattern of 744 plus a cube:
eπ√58=24591257751.9999998222...,
eπ√37=199148647.99997804....,
eπ√22=2508951.998257...,
There are far more than the statistically-expected number of occurrences of eπ√N falling within 1/100 of an integer for integer N: 11 occurrences for N<100 and 37 occurrences for N<1000. Many are listed in my entry for eπ. The first 11 all fall just below an integer value (giving two 9's after the decimal point), and then we start getting a mix of just-below and just-above values. See OEIS sequence A19296, or here for a list.
You have to get into some very deep mathematics to show why these "almost integers" occur, but the end result is that for certain values of N, if A=eπ√N),
A - 744 + 196884/A - 21493760/A2 + 864299970/A3 - ... = B3
where B is some large integer (such as 96, 960, 5280 and 640320 in the above examples). If A is large enough, then all the terms after the first two are real small and that means that A has to be real close to an integer.
Amazingly, the above expression and its coefficients are related to group theory and Fermat's Last Theorem. The coefficients are OEIS sequence A0521. All of them (except for 744) are related to terms in OEIS sequence A1379, the degrees of irreducible representations of Monster group M: 196884=196883+1; 21493760=21296876+196883+1; 864299970=842609326+21296876+2×(196883+1); ... See also 196883.
See also 0.392699... and 403.428775....
(age of the universe in seconds)
The age of the universe in seconds. See also 8.03×1060.
897612484786617600 ≈ 8.976125×1017
This number is 28×34×52×72×11×13×17×19×23×29×31×37, and it is the first number with more than 100000 divisors (a highly composite number). Specifically, it is the 155th highly-composite number (counting 2, 4, and 6 as the first three).
It came up in a discussion about 195643523275200 with Raphie Frank98. Noticing that it has 103680 divisors, which is 2 less than a Lucas number, he then found each of the following relations, where LN are the Lucas numbers, TN the triangular numbers, HN are the highly-composite numbers (A2182) and d(HN) is the number of divisors of HN :
d(H-1) + d(H-1) = 0+0 = L0-2 = 0
-1 - -1 = 0 = 2T-1 = -12 + -1
d(H30) + d(H30) = 160+160 = L12-2 = 320
30 - 30 = 0 = 2T0 = 02 + 0
d(H24) + d(H36) = 96+224 = L12-2 = 320
36 - 24 = 12 = 2T3 = 32 + 3
d(H-1) + d(H155) = 0+103680 = L24-2 = 103680
155 - -1 = 156 = 2T12 = 122 + 12
Such patterns exist throughout number theory, and Mr. Frank excels at finding some of the lesser-known ones (for example, see his illustrations on Flickr here and here).
Mr. Frank also pointed out that 103682 appears as the (asymptotic) ratio between alternating members of the sequence of numbers that are both triangular and "heptagonal" (Sloane's A46194) — for example, 593128762435 / 5720653 ≈ 103682.003. He then noted some relationships between the Lucas numbers and the lattice sphere-packing numbers (like 24, 240 and 196560) and referred me to the unique regular tiling of heptagons on a finite symmetrical surface, in which 24 heptagons cover the surface of a three-hole torus (or tetrahedral tube cage) known as Klein's Quartic[196]. This is a 2-dimensional surface (manifold) embedded in 4 dimensions, with 24-fold rotational symmetry, and defined by x3y+y3+x=0 with x,y complex.
First page . . . Back to page 16 . . . Forward to page 18 . . . Last page (page 25)
Quick index: if you're looking for a specific number, start with whichever of these is closest: 0.065988... 1 1.618033... 3.141592... 4 12 16 21 24 29 39 46 52 64 68 89 107 137.03599... 158 231 256 365 616 714 1024 1729 4181 10080 45360 262144 1969920 73939133 4294967297 5×1011 1018 5.4×1027 1040 5.21...×1078 1.29...×10865 1040000 109152051 101036 101010100 — — footnotes Also, check out my large numbers and integer sequences pages.
 s.27
s.27