Sequences Related to the Work of Srinivasa Ramanujan
As Matt Parker described in this video, the "taxicab number" 1729 (equal to 103+93, and also to 123+1) appears in "Ramanujan's lost notebook", along with formulas for a lot of similar but larger numbers.
Amazingly, though these formulas have been discussed extensively and some of the formulas have been iterated beyond Ramanujan's examples, half of them have not been extended, including the ones of which 1729 is the first example. See the references section for details.
The "lost notebook" page in question is what I'm calling "page 82", because there is a circled "82" in the upper-right corner. It is p. 341 in the 1988 book [3], and an image is below.
Ramanujan wrote:
|
I'll refer to the terms a0, a1, a2, a3, ... as Ramanujan's "a-series". They are the coefficients of a Taylor series, which is a power series in positive exponents of x that approximates the ratio of polynomials on the left side of equation (i), and which converges when x is near 0. The first three terms are 1, 135, and 11161. Once the first three are known, the rest can be computed by the recurrence relation:
an = 82an-1 + 82an-2 - an-3
For example, 82×11161 + 82×135 - 1 = 926271. The sequence is in Sloane's database as A51028 : 1, 135, 11161, 926271, 76869289, 6379224759, 529398785665, 43933719985479, ...
Since their generating functions have the same denominator 1-82x-82x2+x3, we know that the b and c coefficients can be computed the same way. In the OEIS they are:
A51029 : 2, 138, 11468, 951690, 78978818, 6554290188, 543927106802, 45139395574362, ...
A51030 : 2, 172, 14258, 1183258, 98196140, 8149096378, 676276803218, 56122825570732, ...
As Ramanujan shows in his examples, the a, b, and c numbers can be combined to give equations in which the sum of two cubes is equal to another cube, plus or minus one. For example, 1353 + 1383 = 1723 - 1.
A limited number of terms can also be computed by the "magic decimal digits" method that I describe here, wherein one substitutes a very small power of 10 (like 10-10) for x, and then computes the decimal digits of that ratio of polynomials. For example, the a-series:
if x = 10-10,
(1+53x+9x2) / (1-82x-82x2+x3)
= 1.0000000135000001116100009262710076869289...
The other coefficients, which Ramanujan calls by the Greek letters α, β, and γ, are also power series coefficients, but this time the terms of the power series have negative exponents of x. These power series converge only when x is "near infinity", that is to say, when x is far from 0.
We can think of these coefficients as being the terms of a, b and c that come "before" the terms we computed above, and to do that we just turn the recurrence relation around:
if
an = 82an-1 + 82an-2 - an-3
then
an-3 = 82an-2 + 82an-1 - an
for example to get a-1 we can compute 82a0 + 82a1 - a2 = 82×1 + 82×135 - 11161 = -9. Continuing likewise, the sequence a-1, a-2, a-3, ... is:
αn = -9, -791, -65601, -5444135, -451797561, -37493753471, -3111529740489, -258219474707159, -21429104870953665, ...
These are clearly Ramanujan's α coefficients with minus signs. (Without the signs, they are OEIS sequence A272853.)
Similarly we can compute the β and γ series, except that we do not get minus signs:
βn = 10, 812, 67402, 5593538, 464196268, 38522696690, 3196919629018, 265305806511788, 22017185020849402, ... (A272854)
γn = 12, 1010, 83802, 6954572, 577145658, 47896135058, 3974802064140, 329860675188578, 27374461238587818, ... (A272855)
Combined, the α, β, and γ numbers give us additional examples of two cubes that sum to almost another cube. For example, 7913 + 8123 = 10103 - 1.
Notice that that the β terms come from reversing the c-series:
-14258 + 82×172 + 82×2 = 10
-172 + 82×2 + 82×10 = 812
-2 + 82×10 + 82×812 = 67402
etc.
and similarly, we get the γ terms by reversing the b-series:
-11468 + 82×138 + 82×2 = 12
-138 + 82×2 + 82×12 = 1010
-2 + 82×12 + 82×1010 = 83802
etc.
Using Wolfram Alpha to ask for the Laurent series (put in Series[-1*(2-26x-12x^2)/(1-82*x-82*x^2+x^3), {x, Infinity, 10}] for b, and put in Series[-1*(2+8x-10x^2)/(1-82*x-82*x^2+x^3), {x, Infinity, 10}] for c) also shows this reversal.
Ramanujan seems to have switched β with γ in the final statement, which "should" be:
αn3 + γn3 = βn3 + (-1)n
I say "should", because Ramanujan probably would not have made such a simple mistake, and yet it's clear that, for example, 7913 + 10103 is nowhere near 8123.
To see what happened, let's restore the unexplained minus sign to the α series coefficients, and leave β and γ as Ramanujan wrote them. If we also change the sign before the (-1)3, we get this:
-αn3 + βn3 = γn3 - (-1)n
which is equivalent to the "should be" version above. For example, -7913 + 10103 = 8123 + 1, which is just a different way of saying 7913 + 8123 = 10103 - 1. So Ramanujan was simply rearranging things to avoid the minus sign but forgot to switch the letters.
You can verify this for yourself. First, see the original in Ramanujan's writing.
Then convert the generating functions into a series sum of negative powers of x. There are four ways to do this:
1. Laurent series expansion with symbolic maths software. Use Wolfram|Alpha with the input expressions I gave above. Similar commands should work in Mathematica.
1b. I have Maxima, which generates Laurent series with a command like "taylor((1+53*x+9*x^2)/(1-82*x-82*x^2+x^3),x,inf,10);". This is the same command one would use for a Taylor series, but with inf in place of 0 for the 3rd argument.
2. Reverse the recurrence formulas, as shown above, to derive the terms of the an, bn, and cn series terms for negative n.
3. Perform "long division" to on the polynomials 2-26x-12x2 / by 1-82x-82x2+x3, with the order of the terms reversed so that the highest power of x is on the left:
|
4. The α, β, and γ series terms can also be seen by substituting a large power of 10 for x and evaluating the generating function's polynomials numerically to high precision. For example, if x=1010 we get:
(1+53x+9x2) / (1-82x-82x2+x3) = 0.0000000009000000079100000656010005444135...
(2-26x-12x2) / (1-82x-82x2+x3) = -0.0000000012000000101000000838020006954572...
(2+8x-10x2) / (1-82x-82x2+x3) = -0.0000000010000000081200000674020005593538...
The first set of three highlighted coefficients give the famous relation 93+103=123+1; these and the next two sets are given as examples in Ramanujan's notebook; the 4th set represents the relation:
54441353 + 55935383 = 69545723 - 1
The Mysterious 6th Example
Another oddity is Ramanujan's example "63 + 83 = 93 - 1". It is similar to all of the others, but the numbers 6, 8, and 9 do not appear as coefficients in any of the power series. It is certainly true: 216 plus 512 is 728, one less than 729. Also, we can combine it with the 1729 sum to give the nice identity
63 + 83 + 103 = 123
which is just a slightly-obfuscated way to say 33 + 43 + 53 = 63 (see the 216 entry in my Numbers pages).
Also, Ramanujan does not cite the trivial example "13 + 23 = 23 + 1" which comes from the very first terms of the a, b, and c series but is of no interest as a Fermat near-miss.
Among these references, all that mention Ramanujan pertain only to the a-, b-, and c-series. Amazingly I have found nothing online (except on this page and my numbers pages) about Ramanjuan's α, β, or γ series and that explicitly give terms beyond those in Ramanujan's notebook.
[1] N. B. Mitra, Replies to Questions. The American Mathematical Monthly 32(10) pp. 506-509 (Dec. 1925).
Gives the (α,β,γ) tuples (5444135, 5593538, 6954572) and (451797561, 464196268, 577145658) and the (a,b,c) tuple (76869289, 78978818, 98196140) but without reference to Ramanujan or his formulae.
[2] D. H. Lehmer, On the diophantine equation x3+y3+z3=1. Journal of the London Mathematical Society 31 pp. 275-280 (1956).
Gives the same three tuples as [1], again without reference to Ramanujan or his formulae. Also gives the unrelated huge tuple (1349622603595589672, 1964429523102862535, 2157232752187946774).
[3] S. Ramanujan, The Lost Notebook and Other Unpublished Papers (1988), p. 341. New Delhi (Narosa publ. house).
[4] Michael D. Hirschhorn, An amazing identity of Ramanujan. Mathematics Magazine 68(3) pp.199-201 (Jun 1995). MR1335148
[5] Michael D. Hirschhorn, A Proof in the Spirit of Zeilberger of an Amazing Identity of Ramanujan. Mathematics Magazine 69(4) 267-269 (Oct 1996).
[6] Michael D. Hirschhorn, Ramanujan and Fermat's Last Theorem (2004).
[7] Jung Hun Han and Michael D. Hirschhorn, Another look at an amazing identity of Ramanujan. Mathematics Magazine 79(2) pp. 302-304 (Oct 2006).
Ramanujan's "Lost Notebook", page 82
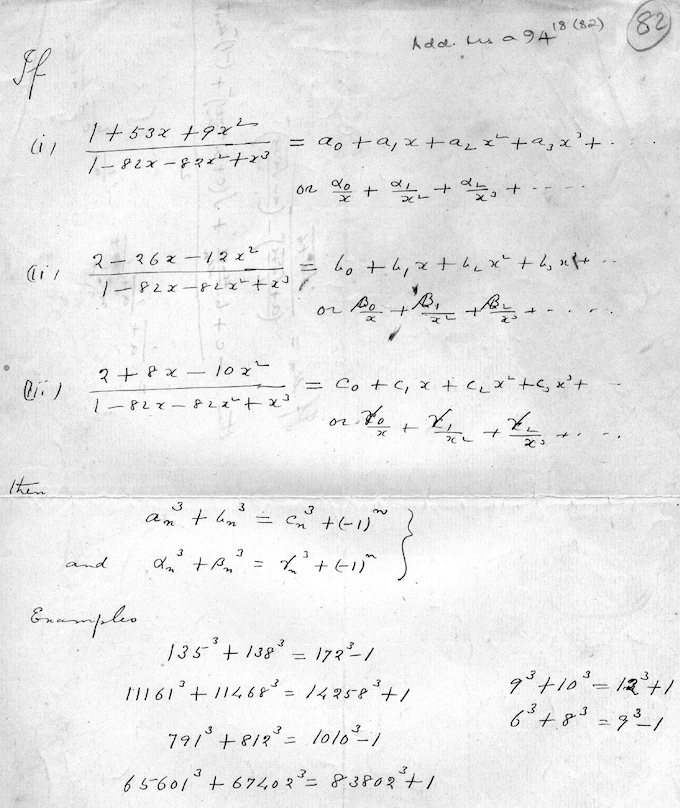
This page was written in the "embarrassingly readable" markup language RHTF, and was last updated on 2022 Mar 28.
 s.30
s.30