U-Skate World, an Instance of the Gray-Scott System
Contents
Early, Middle and Late-stage Evolution
Uskate World in 1 and 3 Dimensions
![]()
The reaction-diffusion hacker emblem
The Gray-Scott system produces a wide variety of interesting patterns and behaviour, such as cells that multiply, self-organising fingerprint patterns and much more. Most of these have some variety, for example I have seen 4 different patterns of cell division.
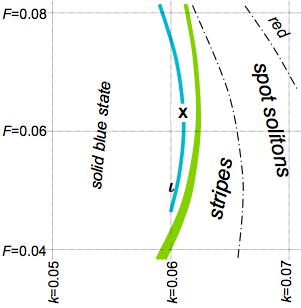
However, one particular area of the parameter space exhibits patterns with at least as much diversity as Conway's Game of Life and similar systems. This region is indicated by the narrow blue line in the figure on the left, which schematically represents a section of the parameter space in Gray-Scott reaction-diffusion systems:
|
The images on this page show some of the more common patterns; there are also some illustrations for my 2009 paper and a fairly large collection of stable patterns here: catalog/gallery of patterns.
I refer to this particular system (Gray-Scott using the Pearson constants and F=0.0620, k=0.0609) as U-skate world because of the skate, the U-shaped, common, persistent moving object seen in some of the examples below.
I showed some of these patterns in a talk at Rutgers as part of their Mathematical Physics seminar series, fall 2010. The slides and notes are avaiable here: Munafo 2010 Stable (Rutgers talk)
The most common stable shape is a negaton, or negative soliton. A true negaton has a circular shape that can exist in any large blue (low U, high V) area. The more common "negative solitons" mentioned in most of my Gray-Scott parameter descriptions (such as here and here) are really just a roughly circular interior of a loop.
First true negatons
Negatons exist at many parameter values near the western (low k) edge of the complex region identified by Pearson. At the very westernmost parameter values they are stable (viable) only if they have one or more other negatons as neighbors. This video shows the behaviour at (F=0.0460, k=0.0594), described more fully here. It is the first place I found true stable negatons.
In the "U-skate world" parameters discussed below, negatons survive indefinitely in isolation, and also tend to clump together in groups. They exhibit a behaviour similar to bubbles in water with "surface tension", moving more quickly when they get close to contact, and holding back the movement of other shapes such as those discussed below.
First convincing evidence of class-4 complexity
Above is a video of the behaviour at (F=0.0620, k=0.0609) that made me believe I would find phenomena as complex as a Wolfram "class 4" cellular automaton.
U-Skate Discovery Video
In the early morning of 2009 March 23rd I saw the U-shaped moving pattern for the first time. This is the first simulation that I made a recording of. (2009 March 23rd at 3:25 AM).
The skate or U-skate is a moving shape that keeps its form and moves indefinitely if unimpeded.
Mapping out the region
The above simulation shows a range of parameter values; higher F is near the top; higher k is near the right. Based on this and some other similar tests, I decided to move down to F=0.0600.
Early, Middle and Late-stage Evolution
Diverse behaviours over different time scales
This is an "accelerating time-lapse" video with a simulation rate that increases progressively: the simulated speed doubles every 7 seconds.
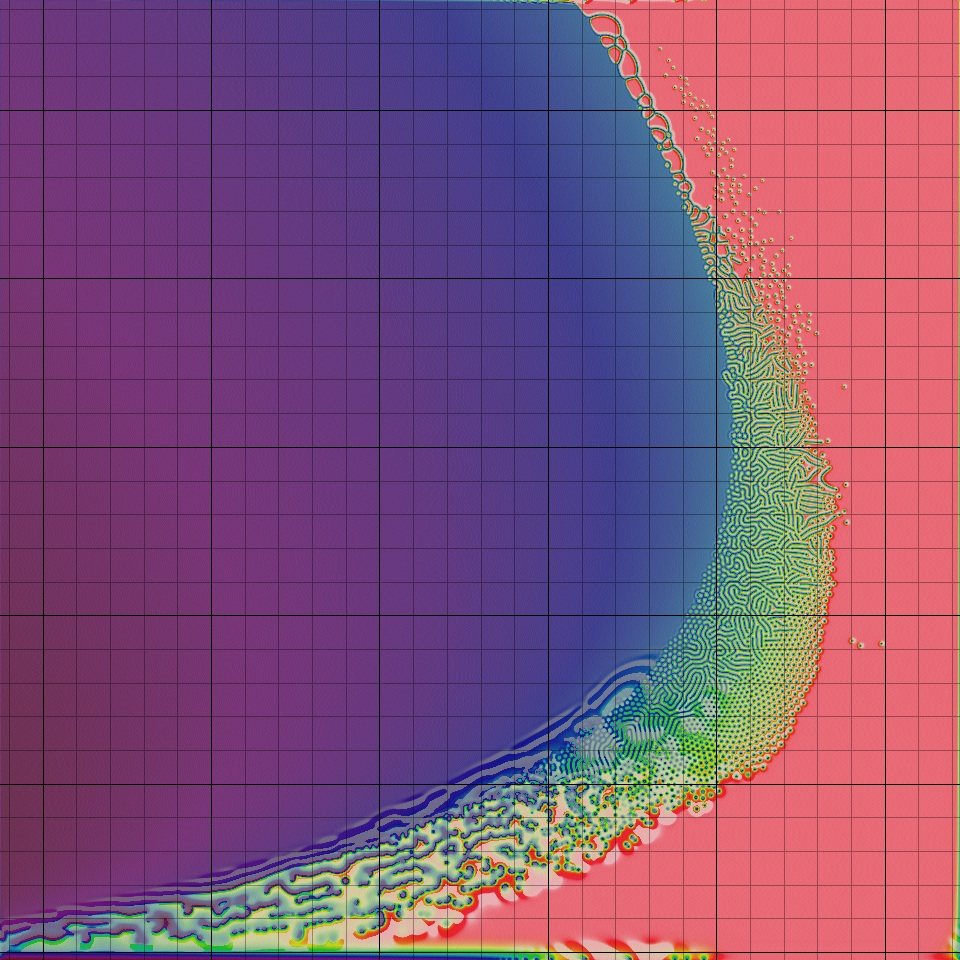
0:00-0:40 Fixed-rate growth : First we see normal growth of blue spots to mostly fill the space, leaving some spots and stripes and a lot of solid blue. Some stripes shrink to spots. This is very similar to the early evolution of Gray-Scott systems at many other F and k parameter values.
0:40-1:15 Complex behaviour, first stage : Once the field is mostly blue with stripes and spots, the pattern starts to evolve in ways that exhibit both orderliness and unpredictability. Any remaining stripes gradually bend, alternately lengthen and shrink, and start to create parallel features. Pause the video at 1:12, and you can see a bunch of closely-spaced yellow stripes in the lower-left, and a pair of yellow stripes at a wider spacing in the bottom-center.
1:15-1:29 Complex behaviour, second stage : At about 1:15 there are few solid blue regions left, and the system switches to a different type of behaviour that is both orderly and unpredictable. Groups of parallel stripes "compete" with one another in complex ways. At times the space is completely filled by stripes and negatons; at other times areas of solid blue open up.
1:29-1:42 Stability : At 1:29, all chaotic activity immediately and permanently stops. This is very similar to the fate of large fields of chaotic activity in cellular automata like Conway's Game of Life. The final state contains stripes, negatons, and a region of solid blue, and it is qualitatively similar to the chaotic states that led up to stability.
The only remaining motion is a continuous "drift". This drift is very slow, but here appears to accelerate because of the accelerating time-lapse nature of the simulation. The direction of drift is related to the shape and orientation of the curved stripes.
Uskate World in 1 and 3 Dimensions
Using the same parameter values, it is possible to create stable moving patterns in 1-, 2- or 3-dimensional Gray-Scott systems. Here is an image comparing 1D and 2D patterns made solely of spots:
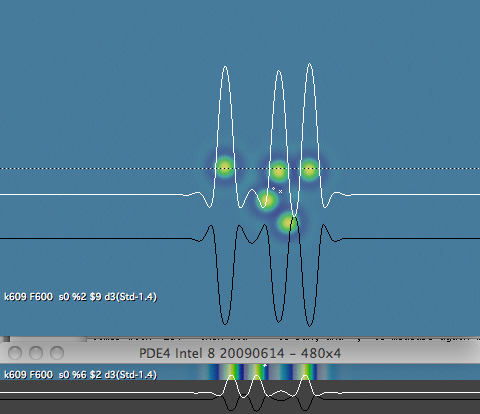
Here are two moving patterns in 3D. The one on the right was discovered by Tim Hutton and moves in a straight line. The other is the same but with just one spot added, which makes it travel in a helical path. As shown here, both are moving up:

Their closest analogues in 2D are these two "halftargets" (from my gallery):

Tim Hutton soon discovered several other patterns, such as these based on the annulus ring and similar to the 2D "target" patterns:
Hutton's 3D ring gliders
This page was written in the "embarrassingly readable" markup language RHTF, and was last updated on 2016 Jul 04.
 s.27
s.27