Correspondence with Ivan Freyman

Subject: Re: Mariani-Silver
From: Robert; Date: 2004 Feb 27

Thanks for writing back!

I could think of only three simple geometric shapes that can be subdivided into smaller copies of themselves. A parallelogram, a triangle, and a square divided into four equal parts with one quarter missing, which forms a six-sided shape.

Take a regular hexagon, draw a line from one vertex to an opposite vertex to divide it into two pieces. Each half is a 4-sided figure, a trapezoid, 4 of which can be joined together into a larger copy. Sometimes at elementary schools, daycare centers or libraries you will see tables shaped like this that have been moved together to make one bigger table. Using a monospace font like Courier or Andale Mono, it looks like this:

________ /\ /\ / \____/ \ / / \ \ /___/______\___\

I think this shape, or a full hexagon made from two of these, would make a beautiful Mariani-Silver fractal.

If you slice the figure vertically down the middle, you get a figure with two half-trapezoids and one intact trapezoid. Divide the remaining intact trapezoid down its axis and you get a figure like this, which is another solution. The edge lengths of the piece are 1, 1, 1/2 and sqrt(3)/2, and the edges of the whole figure (4 pieces) are 2, 2, 1, and sqrt(3):

____ | /\ |__/ \ | \,-'\ |___\___\

There are other similar shapes, all made from multiple equilateral triangles. Such shapes are called "polyiamonds", because two equilateral triangles is a "diamond", so three is a "triamond", etc. Here is the next one that tiles into itself, a hexiamond:

/\ / \ / \ / ___\________ / /\ /\ /___/ \ ____/ \ / \ / \ /__________\/__________\

There are non-integer ways to divide certain triangles. For example, slice an equilateral triangle in two halves; three of these can be made into a larger replica:

.. |\'-. | \ '-. | \ /-. | \ / '-. |____\/_______'-.

Other 6-sided "L" shapes, similar to the one you already found, can be formed that tiles itself. One is a tetromino, its edges, in order clockwise, are length 1, 1, 2, 3, 1, 2. The other is a pentomino, with edges 1, 1, 1, 3, 2, 2:

___ ___ |_ | | | | | | ___|_ | | |_| |_ |_| |___|___ | |___| | | ___| | | | | |_|_____| |___|___|

A trapezoid with sides length 1, 1, sqrt(2), 2, tiles itself. This is a different arrangement from either of the two above trapezoid solutions:

/| / | /| | / |___| | | | |___| | | \ | |______\|

The above shapes, plus the ones you already knew about, and "linear transformations" of these (which includes ordinary stretching along one or both axes, and the transformation that turns a square into a rhombus) comprise all currently-known shapes that replicate themselves by breaking one up into 4 copies. Together they are called "reptiles of order 4".

There are many higher-order reptiles, including orders of n² (like 4 and 9) and others like the above example, the half-equilateral triangle which is an order 3 reptile. Here's just one order-9 example: a polyiamond made from 8 triangles:

____________ / / \ / / \ /\ / \ / \ /__________\ / \ / \ \ / \/ \ \ / / \ /\ /_______/__________\ / \ / \ / \ / \ / \ / \/ \ / \ / \ \ /__________\____/__________\_______\

For more details, go to:

Poly Pages: Reptiles

Cyclomers (2D)

I noticed on your website that you still have the part about Mariani-Silver requiring recursion and a stack of arrays. (See "Best algorithm for the job" [...]

Oh, yes, thank you! It's hard for me to find all the references to a given concept... )-:

Anyway, thanks for having such a great informative site regarding the Mandelbrot set.

You're welcome, and further corrections are always welcome!

(The rest of this message concerned extropianism, theoretical limits on computing, and properties of black holes.)

(several messages omitted)

Subject: Pentagonal Mariani Silver
From: Ivan; Date: 2004 May 6

Hi Rob, this is Ivan. I wrote to you re: the MS algorithm and you provided me with some great self-replicating tile ideas.

So far I've done a square:

http://www.armcorp.us/site/square.gif

an isosceles right triangle:

http://www.armcorp.us/site/TriRight.gif

an equilateral triangle:

http://www.armcorp.us/site/TriEq.gif

a trapezoid:

http://www.armcorp.us/site/trapezoid.gif

and now finally a pentagon. Well, sort of.

As you know, if a regular pentagon is subdivided into five smaller ones, triangular "holes" are left behind. I figured I could fill these holes with Sierpinski triangles. Since a Sierpinski triangle also has holes, I filled them as well to ensure a complete, solid figure.

Anyway, the link below shows four pentagons subdivided in this manner, with successive increments in the number of subdivisions.

http://www.armcorp.us/site/pentagon.gif

I combined that subdivision algorithm with a 4th-degree Newton's method Julia fractal, and got the picture below:

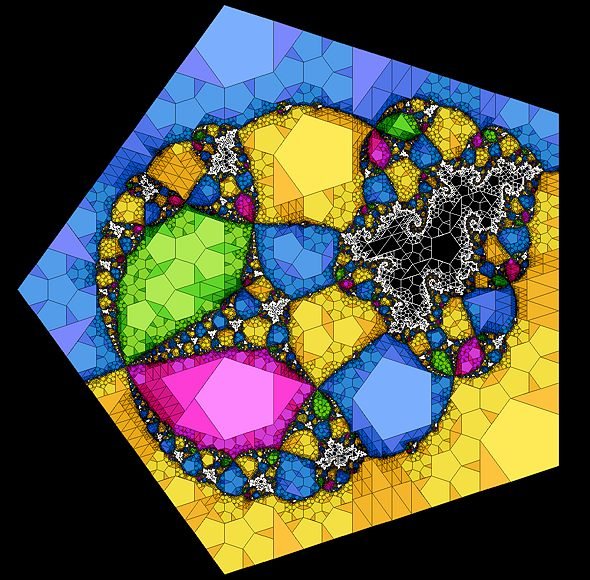
http://www.armcorp.us/site/PentNewt.jpg

I tried replicating your 2nd-order embedded Julia set called "Munafo Minibrot" with the distance-estimator method, but my programming language limits me to 16 digits of precision. Is there some trick for getting a bit more precision without writing an arbitrary-precision routine like in FractInt ?

Thanks.

Ivan's pentagon tiling can be modified by placing the largest possible pentagon inside the 36-72-72 triangle. The result is this 2-rule substitution tiling:

$A simple modification of Ivan's pentagon tiling$
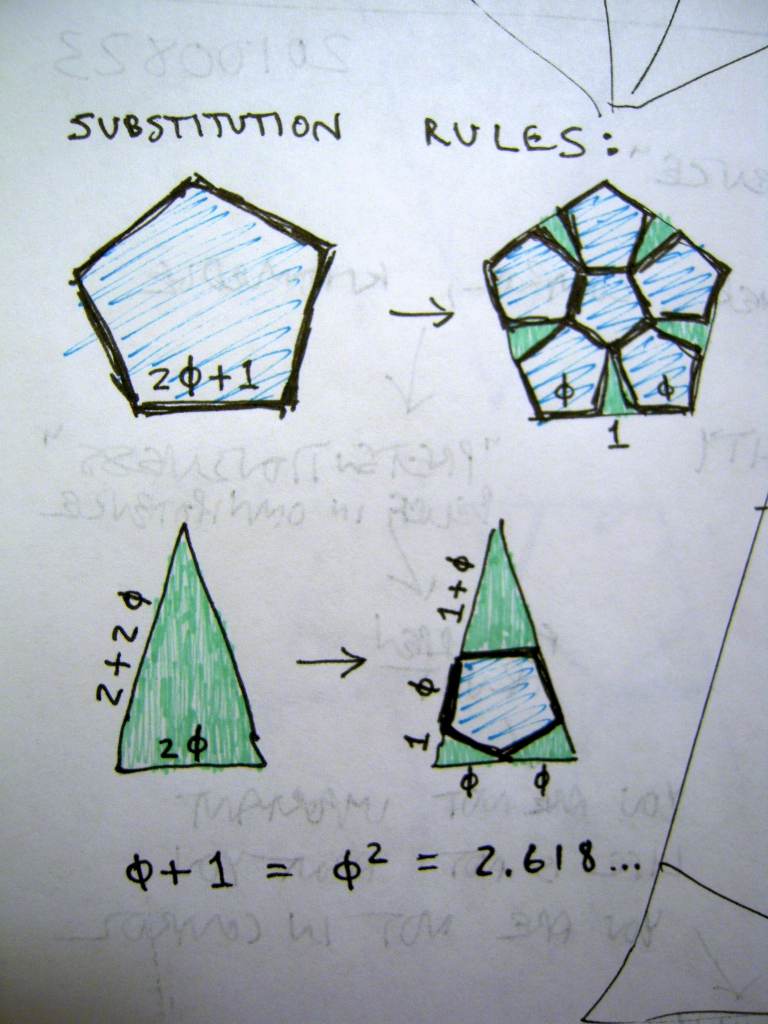
A simple modification of Ivan's pentagon tiling

As the rules are applied numerous times, each edge length is of the form Φ^A2^B with A,B being integers.

Subject: Pentagon tiling
From: Robert; Date: 2004 May 7

Hi Ivan!

Your pentagon tiling is great, and beautiful. I confess that I abandoned my project for something else, and never finished adding the iteration code to make it draw a fractal image on the grid.

If you are interested in a result that includes more pentagons, I would suggest dividing the triangle in a way that includes a pentagon.

Suppose the pentagon you start with has sides of length Φ³ = 4.236. When you divide it you get 6 pentagons with sides length Φ=1.618 and 5 acute icosceles triangles (with sides of length 1, 1.618, 1.618) which I'll call "type A".

You have been dividing the type A's into 4 smaller type A's, with sides half as long (0.5, 0.809, 0.809). Instead I propose you should divide it into 3 smaller type A's (with sides 0.382, 0.618, 0.618), a pentagon (all sides 0.382) and a "type B" triangle, an obtuse isosceles with sides 1, 0.618, 0.618. These are arranged in such a way that the pentagon and the three type A's form a 5-pointed star with two points missing.

The type B triangle is shaped like the top 1/3 of a pentagon and can be further divided in the same way the top part of your original pentagon was divided, which gives a pentagon (sides 0.236), two type A triangles (sides 0.236, 0.382, 0.382), and two smaller type B triangles (sides 0.382, 0.236, 0.236).

$Penrose-related tiling with 3 rules$
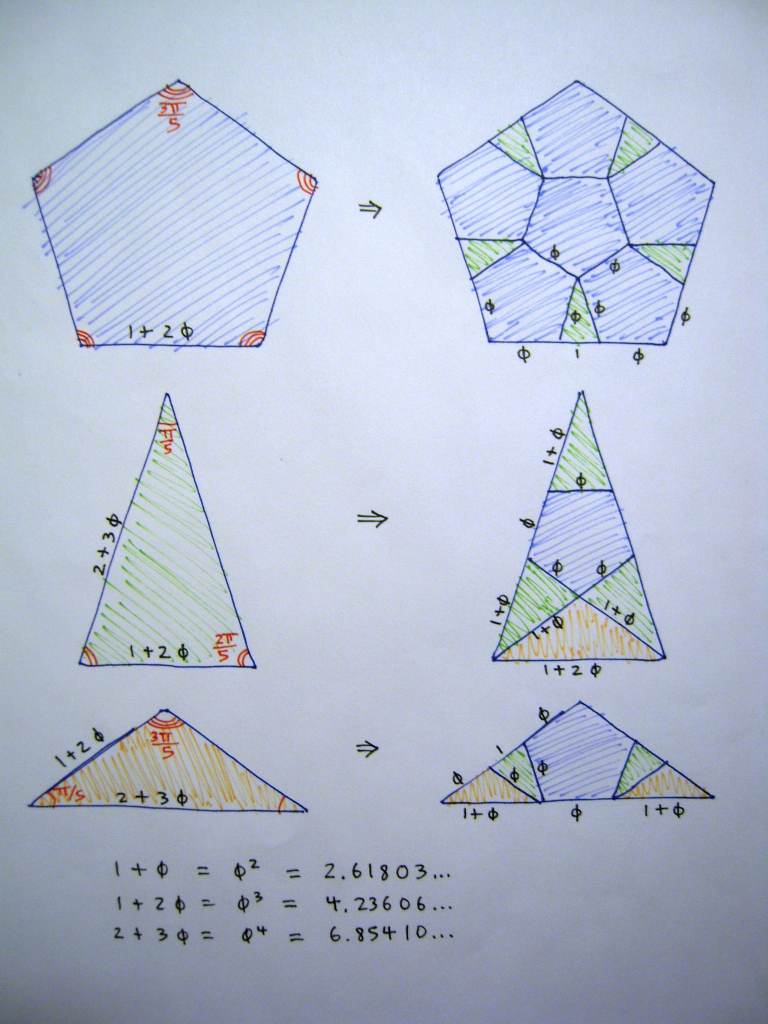
Penrose-related tiling with 3 rules

Notice that all of the numbers I have used here are powers of phi: Φ³, 1.618=Φ, 0.618=1/Φ=Φ^-1, 0.382=Φ^-2, and 0.236=Φ^-3. This is better in my opinion because it avoids involving powers of 1/2 like you get with your system. It also avoids having big regions with no pentagons.

Penrose tilings are the simplest way to get 5-way rotational symmetry. Here are two good pages showing the patterns and the method of generating them:

http://goldennumber.net/penrose.htm

http://www.stephencollins.net/web/penrose/

- Robert

Subject: P.S. (high precision)
From: Robert; Date: 2004 May 7

Hi again — I forgot your other question.

I used an object-oriented language, C++, to make my high-precision programs. I have created two high-precision floating-point data types using C++'s operator overloading. (I also have 64-bit and 128-bit integer data types which I use for certain other things, like my work with integer sequences.)

A followup comment about the pentagon/triangle tiling: The type-A divides into the pentagon and three smaller type-A's which together form three points of a five-pointed star. The other two points are actually present in most cases, because the original type-A triangle is between two pentagons and those pentagons get divided in a way that produces smaller type-A triangles, which end up being the same size as the 3 just mentioned, and positioned properly to complete the 5-pointed star.

- Robert

This page was written in the "embarrassingly readable" markup language RHTF, and was last updated on 2023 Jul 03.

s.27