Integer Sequences Related to 3X+1 Collatz Iteration
(The 3X+1 sequences are also discussed here: A006877, 3X+1 Problem.)
The "3X+1 problem" has been around for a long time, but I learned about it from Douglas Hofstadter's book Gödel,_Escher,_Bach [3]. The Tortoise (in a dialogue with Achilles) presents the problem of determining whether a number is "WONDROUS". He presents the rules thusly:
Choose a starting number X (a positive integer).
If X is ODD, triple it, and add 1,
but if X is EVEN, take half of it;
Repeat this process.
If a starting number eventually reaches 1 then we call it
WONDROUS, and otherwise it is UNWONDROUS.
Achilles chooses the starting number 15 and gets to 1 in 17 steps. The Tortoise, ever the trickster, then suggests starting with 27. The discussion ends with Achilles guessing that as of yet, no one knows of a test for the property of wondrousness which is guaranteed to terminate..
Indeed, such a finite-length test remains unknown, but it would be easy if the Collatz conjecture (posed in the 1930s by Lothar Collatz) could be confirmed.
To formalize the problem a little more,
The starting number is W = X0
If Xn is even, Xn+1 = Xn/2
If Xn is odd, Xn+1 = 3 Xn + 1
The "step count" S(W) is the lowest value of n for which Xn=1, or
(by convention) -1 if there is no such n (OEIS sequence A6577)
The "peak value" P(W) if the highest value of Xn attained
during iteration, or -1 if there is no such highest value (OEIS sequence
A25586)
The central question asks for a proof, or disproof, of the Collatz conjecture which states that the iteration reaches 1 for every (positive integer) starting value.
If that is true, then it means S(W) and P(W) will never be -1.
You might have already noticed that if the conjecture is not true, it could be for either or both of these reasons:
- Some starting value results in iteration that eventually repeats itself, but without reaching 1 (so S(W) would be -1, but P(W) would be defined), and/or
- Some starting value results in iteration that never repeats and therefore keeps going to ever-higher values (so S(W) and P(W) would both be -1)
Let's try the Tortoise's suggested starting value of X0=27. The values of Xn are:
27, 82, 41, 124, 62, 31, 94, 47, 142, 71, 214, 107, 322, 161, 484, 242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, 700, 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 668, 334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 638, 319, 958, 479, 1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, 7288, 3644, 1822, 911, 2734, 1367, 4102, 2051, 6154, 3077, 9232, 4616, 2308, 1154, 577, 1732, 866, 433, 1300, 650, 325, 976, 488, 244, 122, 61, 184, 92, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1, 4, 2, 1, 4, 2, 1, ...
The value goes up and down many times, and seems to be growing steadily into 3- and 4-digit values, but then quickly goes back to small values and ends with the repeating sequence 4, 2, 1, 4, 2, 1, ...
Some Sequences Related to 3X+1
The most basic part of the 3X+1 problem is the calculation that gets repeated over and over. It is a function that takes an integer and returns another integer as a result. In Python that could be expressed as:
F = lambda x: (3*x+1 if (x%2) else x>>1)
This function is in the OEIS as sequence A6370, with the first term representing F(1):
A006370: 4, 1, 10, 2, 16, 3, 22, 4, 28, 5, 34, 6, 40, 7, 46, 8, 52, 9, 58, 10, 64, 11, 70, 12, 76, 13, 82, 14, 88, 15, 94, 16, 100, 17, 106, 18, 112, 19, 118, 20, 124, 21, 130, 22, 136, 23, 142, 24, 148, 25, 154, 26, 160, 27, 166, 28, 172, 29, 178, 30, 184, 31, 190, 32, 196, 33, ...
As discussed above, we iterate this to see if the value 1 is reached. The most immediate question regards how many steps it will take to iterate. That's sequence A6577, the S(W) function above, with the first term representing a starting value of 1:
A006577: 0, 1, 7, 2, 5, 8, 16, 3, 19, 6, 14, 9, 9, 17, 17, 4, 12, 20, 20, 7, 7, 15, 15, 10, 23, 10, 111, 18, 18, 18, 106, 5, 26, 13, 13, 21, 21, 21, 34, 8, 109, 8, 29, 16, 16, 16, 104, 11, 24, 24, 24, 11, 11, 112, 112, 19, 32, 19, 32, 19, 19, 107, 107, 6, 27, 27, 27, 14, 14, 14, 102, 22, ...
One then often speculates about the highest value reached during such an iteration, called P(W) above. That is sequence A25586:
A025586: 1, 2, 16, 4, 16, 16, 52, 8, 52, 16, 52, 16, 40, 52, 160, 16, 52, 52, 88, 20, 64, 52, 160, 24, 88, 40, 9232, 52, 88, 160, 9232, 32, 100, 52, 160, 52, 112, 88, 304, 40, 9232, 64, 196, 52, 136, 160, 9232, 48, 148, 88, 232, 52, 160, 9232, 9232, 56, 196, 88, 304, 160, 184, 9232, ...
A person's first-time exploration will then often proceed in a manner similar to the excellent Numberphile video UNCRACKABLE? The Collatz Conjecture, in which Brady Haran and David Eisenbud try various starting numbers and write down their "trajectory" i.e. sequence of iterates Xi. Working on paper, and noting numbers that appear as Xi in one iteration and Xj in another, they start to build up a directed graph. If the Collatz conjecture is true, it would be a tree graph with 1 as the root and all directed edges pointing towards the root. For example, their first trial number is 7, leading to the sequence: 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1. We see (in bold) the numbers that also appear in the "trajectory" of 27 above. They soon add the numbers 6, 3, 10, ... and then 9, 28, 14, 7, ... and their discussion contemplates continuing in like manner, always adding the next number that hasn't been seen yet. (The OEIS sequence of which number they should add next is A61641 (1, 3, 6, 7, 9, 12, 15, 18, 19, 21, 24, 25, 27, ...). Let's add the next number they didn't cover in their video, which is 12; and since Achilles' 15 is next we'll add that, and the tricky Tortoise's 27:
Tortoise: 27--82--(many steps)--194--92-. ) ,--------------------------' 12 Achilles: \ \ 15--46--23--70--35--106--53--160--80 6--3 \ \ 9--28--14--7--22--11--34--17--52--26--13--40--20--10--5--16--8--4--2--(1)If one proceeds in this manner, one is likely to wind up in this situation:
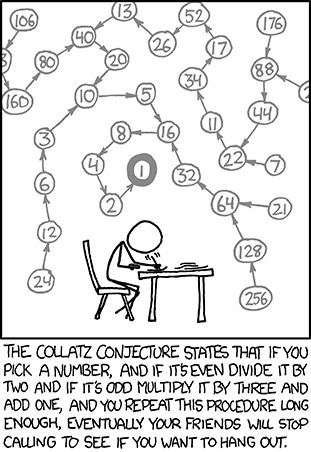
A complete graph would have an edge for each pair of vertices (A6370[i], A6370[i+1]). Viewed as a binary tree (treating 1 as the root and ignoring the cycle 1→4→2→1), any given node can have at most 2 children, one odd and one even. More specifically, node n always has 2n as a child, and has (n-1)/3 as a child only if that is a whole odd number, i.e. only if n=4 mod 6 (and also n is greater than 4, because we're ignoring the 1→4→2→1 cycle).
Suppose we build the full tree graph starting at the root and branch out whenever n=4 mod 6. How many numbers are there at each level of the tree? Or put another way, how many times does each whole number occur as a value of the S(W) function? This is sequence A5186:
A005186: 1, 1, 1, 1, 1, 2, 2, 4, 4, 6, 6, 8, 10, 14, 18, 24, 29, 36, 44, 58, 72, 91, 113, 143, 179, 227, 287, 366, 460, 578, 732, 926, 1174, 1489, 1879, 2365, 2988, 3780, 4788, 6049, 7628, 9635, 12190, 15409, 19452, 24561, 31025, 39229, 49580, 62680, 79255, 100144, ...
This is a Fibonacci-like tree (the number of rabbits in the colony each month, arranged as a hereditary tree) and seems very similar in that each new branch must wait an extra step before spawning a new branch:
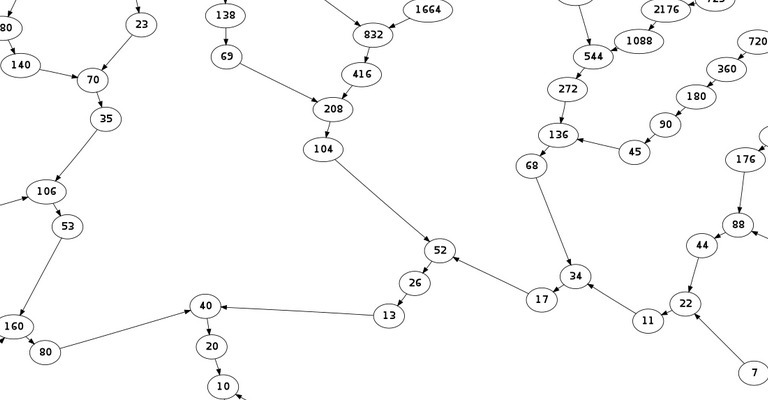
part of the graph
But the numbers here are much different: some branches wait two extra steps before branching again, and odd multiples of 3 become a branch that never creates another odd branch. So there is no simple recurrence relation, and the exponential growth takes a lot longer (as compared to Fibonacci) to settle down to a steady ratio. David Wilson has conjectured the scaling factor per generation to be (3 + √21)/6 = 1.263762615825973...
Record-Setter Sequences
Most starting values end fairly quickly, but a few, such as 27, go for a long time. 27 is a "record-setter" in the sense that its iteration goes higher than any other starting value less than 27. Its P(W) value is 9232. The next record-setter is 255, which goes as high as 13120. Sequence A006885 gives the P(W) values, like 9232 and 13120, and sequence A006884 gives the starting values that set these records:
A006885: 1, 2, 16, 52, 160, 9232, 13120, 39364, 41524, 250504, 1276936, 6810136, 8153620, 27114424, 50143264, 106358020, 121012864, 593279152, 1570824736, 2482111348, 2798323360, 17202377752, 24648077896, 52483285312, 56991483520, 90239155648, 139646736808, 151629574372, 155904349696, 156914378224, 190459818484, 352617812944, 622717901620, 858555169576, 1318802294932, 2412493616608, 4799996945368, 60342610919632, 306296925203752, 474637698851092, 2185143829170100, 3277901576118580, 6404797161121264, 1414236446719942480, ...
A006884: 1, 2, 3, 7, 15, 27, 255, 447, 639, 703, 1819, 4255, 4591, 9663, 20895, 26623, 31911, 60975, 77671, 113383, 138367, 159487, 270271, 665215, 704511, 1042431, 1212415, 1441407, 1875711, 1988859, 2643183, 2684647, 3041127, 3873535, 4637979, 5656191, 6416623, 6631675, 19638399, 38595583, 80049391, 120080895, 210964383, 319804831, ...
One can also search for starting values that take a record number of iteration steps to reach 1 (the S(W) function above). The records for number of steps, and the starting values that set these records, are sequence A006878 and sequence A006877 respectively:
A006878: 1, 7, 8, 16, 19, 20, 23, 111, 112, 115, 118, 121, 124, 127, 130, 143, 144, 170, 178, 181, 182, 208, 216, 237, 261, 267, 275, 278, 281, 307, 310, 323, 339, 350, 353, 374, 382, 385, 442, 448, 469, 508, 524, 527, 530, 556, 559, 562, 583, 596, 612, 664, 685, 688, 691, 704, 705, 744, 949, 950, 953, 956, 964, 965, 986, 987, ...
A006877: 2, 3, 6, 7, 9, 18, 25, 27, 54, 73, 97, 129, 171, 231, 313, 327, 649, 703, 871, 1161, 2223, 2463, 2919, 3711, 6171, 10971, 13255, 17647, 23529, 26623, 34239, 35655, 52527, 77031, 106239, 142587, 156159, 216367, 230631, 410011, 511935, 626331, 837799, 1117065, 1501353, 1723519, 2298025, 3064033, 3542887, 3732423, 5649499, 6649279, 8400511, 11200681, 14934241, 15733191, 31466382, 36791535, 63728127, 127456254, 169941673, 226588897, 268549803, 537099606, 670617279, 1341234558, ...
Notable Patterns
You may have noticed that sequence A6577 above has a lot of repetitions of the same value. That is partly because for any number n of the form 8a+4, the iteration of n and of n+1 will go to the same value after three steps:
8a+4 → 4a+2 → 2a+1 → 3(2a+1)+1 = 6a+4
8a+4+1 → 3(8a+4+1)+1=24a+16 → 12a+8 → 6a+4
Similarly, 14 and 15 take the same number of steps:
14→7→22→11→34→17→52→26→13→40→...
15→46→23→70→35→106→53→160→80→40→...
Notice that one goes up-down-up-down-... while the other does down-up-down-up-... before getting to 52 and 53 respectively, which fit the 8a+4 pattern. Many pairs and triples appear in A6577, and there are a lot of A-B-A-B repetitions like ... 19, 32, 19, 32, ... You may enjoy explaining some of these by finding more patterns like the 8a+4 one.
Computing the Collatz Iteration
I explored this problem using BASIC on an Apple ][, sometime in 1981. My program ran for a few weeks, looking for "record-setters" for the S(W) and P(W) functions. It got as far as S(77031)=350, then stopped at X0=77671, which is the first to iterate higher than 1010. At the time of this writing, a bit over 40 years later, this equivalent program (in PARI/GP written by Charles Greathouse) does the same for me in 2 seconds:
A006577(n) = { my(s); while(n>1, n=if(n%2,3*n+1,n/2); s++); s } step(n,r) = { my(t); forstep (k=bitor(n,1), 2*n, 2, t=A006577(k); if(t>r, return([k,t])) ); [2*n,r+1] } { r=0; print1(n=1); for (i=1, 34, [n,r]=step(n,r); print1(", "n) ) } \\ By Charles R Greathouse IV, Apr 01 2013Here is a Python program that does the same thing, in just about the same amount of run time:
A6370 = lambda x: (3*x+1 if (x%2) else x>>1) r = -1 for n in range(1, 10**5): a=0 ; n1=n while n>1: n=A6370(n); a+=1; if a > r: print(n1, end = ', '); r=a print('...') # By Ya-Ping Lu and Robert Munafo, Mar 22 2024The improvement in execution time (from a few weeks to 2 seconds) is close to what one would expect, but is a couple orders of magnitude slower than what is possible with parallelism, e.g. by using GPUs. According to long time graphics expert Alvy Ray Smith, there has been a roughly 10× improvement every 5 years over the course of his career.
Brute-force searches, i.e. trying each starting value to see what happens, is an "embarrassingly parallel" problem in that it can be broken up into ranges and run independently on separate CPUs. Nevertheless we have by 2024 only verified the Collatz conjecture for starting values up to 1.77×1021 (Barina 2024, see [4]) All X0 up to this number iterate to the values 4, 2, 1.
The patterns mentioned above (such as the 4a and 4a+1 alignment) can be generalised to "sieve" techniques in which one looks at the values Xi modulo a power of 2 (easy on a computer) using lookup tables to catch cases that can be skipped because they'll immediately coincide with another iteration just performed. Another technique looks at the value of Xi+1 modulo a power of 3.
The best algorithms use the ctz (count trailing zeros) opcode, modulo-3k sieves and a few other tricks to test (by iteration) about 2.2×1011 starting values per second. Barbina [4] has been using GPUs and supercomputers with many CPU cores running in parallel, and in so doing they have been able to exceed somewhat the 10×-per-5-years trend; however this is only true if comparing a single home computer in the early 1980's to a much more costly setup today.
Relevance, or Lack of Such
The 3X+1 problem is one of many similar problems involving iteration of an integer value using one of several polynomials that depend on a modulo value (like odd or even). Such iterations are often referred to as Collatz-like. Some notable examples appear in the "algorithms" used by Turing machine programs that set records in the busy beaver problem.
Other aspects of computing theory, such as the general problem of what is "computable" and what types of tasks can be performed in finite time (or, equivalently, in finite memory 1) benefit from the 3X+1 problem in that it serves as an example of a question not known to be answerable in finite time.
Notes
1 : Halting for bounded machines:
Suppose a computing task, designed to emit a true, false, or "undecidable" answer, is known to sometimes require infinite time but is also known to only use finite memory. A flawless deterministic machine is built to perform the task. With a finite memory requirement of k bits (taken to include all aspects of the machine's state) there are only a finite number of states 2k that the memory can have. An auxiliary monitoring machine can be appended, with a k-bit binary counter to keep track of how many steps the program has taken. Another k bits can be used to keep a copy of the original machine's state every time the counter reaches 2k, and if the active state ever equals the copy the program can then know that it is stuck in a loop, and can halt with the answer "undecidable". Better yet, merely running for 2k steps guarantees that some state has been repeated so there is no need to compare current state to some earlier saved version. The decision problem therefore would always be able to stop in finite time, and therefore it does not require infinite time; alternatively any decision problem requiring boundless time must also require boundless memory. The converse is simpler to show: if a decision problem is known to require boundless memory, then it will require boundless time to fill that memory with unending amounts of computed information.
(Adapted from Minsky 1967)
Some other sequences are discussed here.
References
[2] Marvin Minsky, "Unsolvability of the Halting Problem", in Computation: finite and infinite machines (Englewood Cliffs, NJ: Prentice-Hall), 1967. ISBN 0-13-165563-9
[3] Hofstadter, Douglas, Gödel, Escher Bach: An Eternal Golden Braid, Vintage, 1979, ISBN 978-0394745022
[4] David Barina, Computational Verification of the Collatz Problem, preprint on Research Square (2024).
This page was written in the "embarrassingly readable" markup language RHTF, and was last updated on 2024 Mar 24.
 s.27
s.27