Is This Sequence Interesting?
Introduction
As Alonso del Arte so aptly points out [20]:
The question Is this sequence interesting? often is a subconscious shorthand for two other questions:
1. Do other people find this sequence interesting? and
2. Should I send it in to the OEIS?
So I must point out that this article, while ostensibly about the question of its title, is actually meant to address these other two questions. Thus, we must discuss the OEIS.
The OEIS (Online Encyclopedia of Integer Sequences) [16] has grown over several decades from the individual project of its creator Neil Sloane to a huge collaborative database on the Internet. Like any large collaborative resource, there can be much disagreement over what should or should not be included, often leading to rowdy and disorganized debate.
This article continues a public conversation implicit in the earlier and similar articles on the OEIS Wiki, specifically those by Alonso del Arte [20] and Charles Greathouse [21], and a recent (and more private) early 2013 thread among the OEIS associate editors in the OEIS editors' mailing list [24].
Contents
Indications — (why your sequence might be useful)
Cognitive "Kolmogorov complexity"
Contraindications — (reasons it's NOT interesting) :
Half-Baked or Poorly Researched
Reams of Auto-Generated Sequences
Appendix : Examples Used in this Article
Statement of the Problem
OEISF members and Associate Editors frequently grapple with setting and enforcing fair policies, so that they can deal with OEIS submissions that are clearly (or at least suspect) below the level of quality suitable for including in "a mathematics reference work"1 like the OEIS. Efforts to communicate with submitters as to why their submissions are not "suitably interesting" often results in "pinkboxing fights", i.e. flamewars and other behaviour similar to trolling.
During my recent email discussion with other editors, what became most clear is that is is pretty much impossible to define "suitable quality for submission" with anywhere near the degree of effectiveness that we could define, for example, Kolmogorov complexity.
However, there are very many simple definitions for things that clearly make a contribution valuable, and several nearly-as-simple ways to define something that is suspect 7. However many of these easy rules we may find, yet there will (and must) always be a large gray area in between that cannot be decided simply, and must instead use something like consensus and intuition.
Charles Greathouse presented an example of a sequence that could be "rejected without delay" :
%S 345, 3436, 23432, 2, 456548, 234, 7 %N Buy spammo(TM) brand genuine imitation pills!and then said that "somewhere between that and A000040 there is a gray area." Nearly everything lies somewhere between — thus the problem.
To illustrate all my criteria for interestingness (or non-) that I'll set out in detail below, and simultaneously point out my own tendency toward self-contradiction, and the intractability of the problem, I present this table using some of the examples from this article:
|
Part of the problem also comes from the fact that uninteresting clearly does not correlate with rejection from OEIS. Many pretty boring-looking sequences make it, and this leads people into thinking that any boring sequence should qualify. Alonso del Arte [20] explains it well by analogy:
By my analogy to an English dictionary, some of the not-very-interesting sequences added in the early days of the OEIS are boring but necessary words like "the," "about," "lake," "continue." Some of the new sequences are boring and unnecessary words like "duhmazing" and "refudiate."
The work of defining dull, but necessary sequences continues — a good example is A84558, which has been used in other sequences such as A220657 in the definition of sequences that enumerate permutations [23].
My Prejudices
I am not ashamed to admit that I bring a lot of personal prejudices to this issue. It is clear to me that I fail to see value in contributions that most other editors believe are just fine. When I am not careful, I let my prejudices interfere with my ability to be a fair judge in editorial actions, or I let my bias intrude too far into a discussion with contributors or other editors. Clearly if I had founded the OEIS it would have been much less catholic, and thus less suitable as a public general reference. I also seem to feel a self-righteous authoritativeness when I perceive a given sequence as being good, poor, or worthless. The introduction to Hardy and Wright's Theory of Numbers [12] comes to mind:
We have often allowed our personal interests to decide our programme, [selecting subjects] [...] because we found them congenial and because other writers have left us something to say. [...] We may have succeeded at the price of too much eccentricity, or we may have failed; but we can hardly have failed completely, the subject-matter being so attractive that only extravagant incompetence could make it dull.
Unfortunately, my tastes in integer sequences are pretty narrow. In addition I have contrived things that seem of great interest to me, but clearly that is mostly only because I created them (I'll give some examples below). For these reasons (among others) I do fairly little actual editing.
I have so many of these personal prejudices, that perhaps I cannot hope to codify the "good" reasons for nominating or deprecating a submission. I'll have to make do with displaying my prejudices. Since some of these actually bear some relationship to the "good" criteria that others agree on, perhaps somehow the higher purpose will be served, albeit indirectly.
Indications
The Indications are the possible reasons why a submission could be judged as worthy of inclusion in OEIS. A submission might only have one of these qualities and be worthy, or in other cases it might take more than one.
For most of these, there is a flip-side to the argument which I cover below in Contraindications.
I think of a sequence as embodying "objective truth" if we could reasonably expect it to arrive in an interstellar transmission from Vega 6:
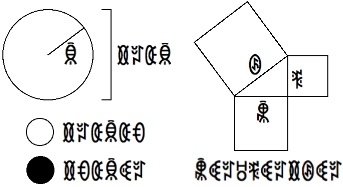
There is a popular belief that most of the mathematics we discover
and consider valuable is equally discoverable and (at least in principle)
would be equally valued by any civilization. [8]
(Actually, my conception of this idea is very "fuzzy": I think truth is less "objectively true" if the notional alien civilization is less likely to stumble upon it on their own. That's really the issue of cultural specificity. I'm probably just misusing the words "objective" and "truth", but I also think I harbor some form of relativism.)
This one's pretty easy: In order for an OEIS submission or addition to be valuable, it must be objectively true. This means that there should be well-defined, and a (perhaps complex) way to demonstrate that the material presented in the submission is correct. The requirement goes all the way back to Rule 4 of Sloane's 1973 book 4.
Most people (by which I mean, not me) who have a serious interest in OEIS use a definition of objective truth which is truly objective: the definition must be precise and unambiguous. That is the sole requirement: it does not necessarily have to be "useful", either to me, or to any other human, or to any alien civilization. Thus, many of the sequences which I consider culturally specific qualify as objectively true. Here's a purely mathematical example:
A(n) = -1 (if n is 0 or negative), the largest prime factor of n (if n is positive and even), 7 (if n is positive and odd).
This is well-defined and unambiguous, and therefore it codifies objective truth, useless though that may be.
Since a lot of submissions merely lack enough clarity to see if it's really true, submitters get frequent requests from editors for better descriptions, clarification, references, supporting data, Mathematica code, and so on. This can be frustrating but it's normal for mathematical work.
By establishing that something is true, we fulfill the first requirement of the submission caveats 1. But truth alone is not enough, particularly if the sequence is culturally specific, or seems arbitrary or contrived.
That Rings a Bell ("Multi-Purpose" sequences)
Many sequences have a dual or multiple purpose:
These illustrations from the Catalan number article on Wikipedia
show two interpretations of the term C4 = 8!/(4! 5!) = 14.
Charles Greathouse [21] gives this as one reason that immediately qualifies something as being "Interesting, probably should be in the OEIS" :
- Apparently unrelated processes generate the same sequence.
Around 1964, N.J.A. Sloane began compiling a database of integer sequences. Initially in written notes and punched cards, the database gradually grew into a collaborative project involving Sloane and many contributors. The original mission or purpose of the OEIS is neatly illustrated by Sloane's introduction to his 1973 book [13]:
Someone coming across the sequence 1, 2, 5, 15, 52, 203, 877, 4140 ... would have had difficulty in finding out that these are the Bell numbers, and that they have been extensively studied. This [database] remedies this situation. — N.J.A. Sloane, [13] preface
This still comprises much of the utility of OEIS: many sequences have been encountered in multiple contexts. For example, A5646 is concerned with how many distinct "20 questions" games distinguish between N distinct things. On suggestion of another seqfan member [19] we broke the problem up so as to create a 2-dimensional grid of numbers (A171872), and I noticed that the main diagonal was A0055 (unlabeled rooted trees). The columns share many terms with other sequences, such as A34189 (the "number of binary codes of length 4 with n words"). Andrew Weimholt and Franklin T. Adams-Watters showed that these conjectures were true [19]. The proof for A0055 involves making a "graph of unique cuts", while the proof for A34189 uses the fact that A034189 can also be interpreted as "the number of 2-colorings of the vertices of the 4-cube having n nodes of one color".
Similarly, A52154 has interpretations related to the lemniscates of the Mandelbrot set, size-2-N divisions of a line segment, and height-limited binary trees.
The possibility of seeing the same thing again in a different context is one of the most compelling reasons for adding new sequences, and new information (e.g. formulas) for existing sequences.
Cognitive "Kolmogorov simplicity"
Perhaps the clearest reason for the popularity and applicability of the Fibonacci numbers is that such a simple definition leads to something with so many interesting properties, and so many connections to other things in mathematics. Sequences like it are appealing to me because of a sense that I'm "getting a lot for my money". With relatively little investment (the iterative formula AN=AN-1+AN-2) I get a whole lot of good stuff.
I think Alonso del Arte [20] and Charles Greathouse [21] sum it up pretty well with the following (from Arte's version) giving three ways that a sequence would be "Interesting and ready for the OEIS"; the relevant two are :
- [It is a] simple function or procedure [that] leads to unexpected results.
- [it is a] neat illustration of a well-known theorem.
If one mathematical phenomenon is useful or commonly used, then a small modification of it is likely to come up somewhere else. Thus, it is common for people (PhDs and hobbyists alike) to invent by taking a sequence that already exists and changing just one bit of the definition. It's much like this cartoon from my favorite strip, xkcd :

Humor through single-point mutation
of a familiar phrase [9]
The single-point mutation is a very common technique for those who create humor. This cartoon, which exemplifies the "words-first" school of cartooning [22], begins with a statement or phrase from everyday life, which in this case was "Objects in mirror are closer than they appear". The cartoonist changes or "mutates" a single thing, in this case replacing closer with bluer. The result is funny (to most readers) 2.
Famous examples among the integer sequences include the Lucky numbers (A000959) which are derived from the primes by a small change to the Eratosthenes sieve algorithm; or the Lucas numbers (A0032) which are like the Fibonacci numbers except that you start with 2, 1 instead of 0, 1; or the "Tribonacci numbers" (A0073) where you start with 0, 0, 1 and each term is the sum of three preceding terms.
Contraindications
Now we get into areas where we want to be more careful. In medicine, a "false diagnosis" can be much more damaging when it is a "false negative" (failing to discover a disease that is actually present), than a "false positive" (thinking a disease is present when in fact there is none) because in general the treatment causes less harm than the thing treated. In the case of OEIS, the opposite is true: If we are trying to judge quality, it is better to wrongly judge some poor sequences as being "good", and include them needlessly, than to wrongly judge some good sequences "poor", and exclude them. Paraphrasing N.J.A. Sloane, there are plenty of A-numbers left and the OEIS search engine seems to do a pretty good job of putting the more popular sequences first when you do a search.
Most of these have an opposite discussed above in Indications.
This is a point made by the simple caveat on the OEIS edit/submit forms 1 which includes this boilerplate inherited from other Wikis:
If you do not want your writing to be edited mercilessly, then do not submit it here.
Antti Karttunen's description of the problem also captures the misunderstanding that many OEIS contributors seem to have, which leads them to get angry when editors either refuse their contributions, or make deletions or other changes later:
We should emphasize that OEIS is not a publishing platform for your personal research, at least not in the same way than say arXiv is. If I submitted a paper to arXiv, and later, long after its acceptance, somebody would start editing its title and the terminology & formulae used in the paper, I guess I would have right to feel indignant. - Antti Karttunen [24]
I maintain a large collection of maths-related material myself, and get occasional submissions from enthusiastic readers. The hardest to deal with are the ones who seem mostly interested in using me as a conduit through which they can publish their own creation (with, presumably, the implied endorsement that comes from it being included with all of my own stuff). If I get the sense that this is happening, I do my best to encourage the reader/would-be-contributor to consider the benefits of publishing it on his own blog or website (Facebook, Google+ and many blogs are free!).
I can give my own creation the Rilybeast breeeding numbers as a good example of something I published purely for personal satisfaction. I simply started with 4 favorite numbers from childhood (3, 7, 27, 143) and used my mcsfind tool to find the (Kolmogorov-) simplest recurrence definition giving those terms. Then I created a vastly embellished science-fiction story to give the sequence some kind of relevance.
Half-Baked or Poorly Researched
Back in the early days, most of what Neil Sloane was collecting had already been published somewhere. A major purpose of the OEIS was to be a sort of index to integer sequences throughout all disciplines of maths and science, pure and applied. Perhaps because of this purpose, or perhaps in an attempt to set a standard of quality, any sequence included in his 1973 book [13] needed to satisfy this "condition of prior publication":4
Rule 4 The sequence should have appeared in the scientific literature, and must be well-defined and interesting.
Back in the old days, a lot of the other reasons I cite here (particularly things like objective truth and avoiding cultural specificity) were taken care of by applying this rule. The few "contrived" sequences (like A0787 which was published in [13] as N1897) had been published in places like Mathematics Magazine or Martin Gardner's column.
Expanding on this (and probably because of confirmation bias on my part), I've always felt that a lot of poor quality stuff gets submitted to the OEIS because the submitter hasn't spent enough time actually making it good. But, creating a web page, blog article, etc. about the sequence can often fix this.
Thus, I tend to believe that if the sequence seems to be of poor quality, it can often be made better if the person would just take the time to publish it on his own, somewhere other than the OEIS. Then, the sequence satisfies the old Rule 4, there is a webpage that can be added as a link in the LINKS section, and who knows? It might even be of better quality too.
Kolmogorov complexity is a measurement of the "complexity" of a mathematical function, computer algorithm, etc. based on how much information (e.g. how many symbols) it takes to describe it. If it takes a big formula or a lot of words to describe a sequence, it is less likely to be interesting. Charles Greathouse described such things as "Sequences with many free parameters and/or arbitrary large constants." [21] and as example stated:
The powers of two is a good sequence, but the powers of 1652 is not.
I have far less tolerance for this sort of thing — I would have immediately rejected A010534 and A200243 (the digits of √83 and of √192 respectively) and I even sometimes doubt the importance of A010465 (digits of √7).
I really love large numbers, and so I like sequences that grow faster and faster as you go along. The Fibonacci numbers A0045 and the powers of two A0079 are child's play, for the number of digits merely grows linearly; I only start getting interested when AN, log(AN), and log(log(AN)) all eventually grow at an accelerating rate.
Around 1990 I started synthesizing sequences that grow slowly at first, then faster and faster. Using recurrence relations one can invent a nearly limitless variety of such sequences. For example, the Fibonacci numbers use the formula c = a+b, because you add any two consecutive terms (a and b) to get the next term (c). My accelerating sequences are a little more complex, for example:
0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 3, 6, 11, 31, 101, 461, 5969,
54970924, 2566256166594610582,
62757193346815419996912506199334550962862239663434039815556137875, ...
the recurrence is
a + b×c + d×ef + g×hi(4)j, where (4)
represents the "lower hyper4" operator.
This sequence has "high Kolmogorov complexity" because you need to string together lots of terms (10 in this case) to make the formula for the next term. About 20 years later I submitted some of my accelerating sequences to the OEIS. Much to my surprise, they were accepted without hesitation (see A171874 and A171877 through A171880).
These examples show that my standard for Kolmogorov complexity is much too strict.
Single-point mutations can yield a lot of useful new sequences, and so they are a tempting way to generate new material. But, just as with real mutations in DNA, most mutations in the creative arts do not make for a very good result 3. If we took every sequence in the OEIS and looked at its definition, we could probably find an average of 20 different "points" in its definition to change, and for each point, perhaps 5 different replacements — yielding 100 variants for each sequence. Surely some of these would be identical to each other, or to sequences already in the OEIS (most added by previous point-mutation propectors!) but there would probably be about 10 variants left, meaning that we could increase the size of the OEIS by a factor of 10 just by adding all single-point mutations. Clearly this isn't a good idea.
Reams of Auto-Generated Sequences
At one point in the 1990's, the OEIS grew by a huge volume due to the addition of thousands of sequences that fit into only a few classes (each defined by a formula with one or two parameters). My pet peeve is A041014 through A042937 inclusive: almost two thousand sequences, comprising the numerators and denominators of the successive fraction approximations to every square root from √11 through √1000. Here's a typical example:
A042345
1, 2, 7, 9, 16, 41, 57, 1466, 1523, 4512, 6035, 10547, 37676,
85899, A042345 4504424, 9094747, 31788665, 40883412, 72672077, ...
Denominators of continued fraction convergents to sqrt(699).
Someone decided this would be useful, and they created a computer program that cranked out 2000 sequences, then bulk-added them to the OEIS.
I feel this kind of stuff is junk. Pick a random number between 41014 and 42937, then go to that A-number in the OEIS, and the odds are really really good that there will be no links to any published references to that sequence (except for Table of n, a(n) for n=0... and Index to sequences with linear recurrences..., both of which were auto-generated).
When I have thousands of sequences to publish, I publish them myself. See MCS: the Minimally Complex Sequences. This satisfies any ego motivation I might have, ensures that the sequences are published first, and keeps the OEIS free of clutter.
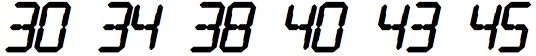
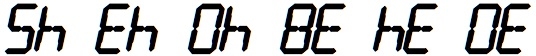
The sequence {10, 14, 15, 17, 18, 30, 34, 38, 40, 43, 45, ...}
consists of numbers which when displayed on a calculator, resemble
words from the Official Tournament and Club Word List when viewed
upside-down. [10]
In my perception, "Cultural specificity" is sort of the opposite of universal truth: some sequences clearly are not of universal interest because they depend on some aspect of the culture or society in which they are viewed. (In fact, universal truth just means it's well defined, and the following examples can easily be well-defined.) Reasons for a sequence being culturally specific include:
- It depends on the numbers being expressed in base 10. This includes nearly any sequence whose description uses the words "digits" or "decimal". Popular examples in OEIS include A36057 (the Friedman numbers), A10888 (additive digital root, aka "casting out nines"), and A2193 (decimal expansion of the square root of 2). These are in OEIS because they're useful, but I hate them anyway.
- It relates in some way to letters or words in English or some other language. Examples include A5589 (length of name of N in English), A139212 (recursively self-defined: A[N] = total number of vowels in the French spellings of A[1] through A[N-1] inclusive) and A124015 (number of words of length N in the National Scrabble Association Dictionary).
- It depends on base 10 or some other base, and also on the written appearance of the digits: examples include A48895 (Primes that are a different prime when turned upside-down, i.e. primes that are in A54047 but are not in A0787). Palidrome sequences like A6995 get a dishonorable mention.
- It relates to some other aspect of popular culture (such as A182369, the decimal expansion of (7(e-1/e)-9)π2, notable solely for beginning with the digits 867.5309 made popular by the song 867-5309/Jenny, which I think is dumb despite that my RIES program was almost certainly used to discover it) or is totally irrelevant outside some small fraction of the Earth's population (such as A0053, street numbers in Manhattan that have a Broadway line subway stop).
Illustrated above is X900012, which combines all of these specificities, and would thus seem to be of nearly microscopic usefulness or appeal — nevertheless, it was something I cared about a lot as a kid.
In my 20's I was really annoyed by these sequences because I felt they had no objective truth. I also didn't like crossword puzzles. As I get older I see that it's sometimes fun to play with words or other things that might not make sense outside my little corner of the world.
Appendix : Some Examples From the Article
For nostalgia, these are conveniently arranged lexicographically as in [13]. I refrained from altering terms as in 4.
a(n) = a(n-1) + a(n-2)a(n-3) + a(n-4)a(n-5). (A171874)
0, 0, 0, 1, 1, 2, 4, 7, 16, 46, 174, 3311, 268446771, 401906756202069927727330981, ...
This is a sequence I invented around 1990 or 1991 and left in a notebook for about 20 years. It is an example of something I think is way too arbitrary and complex to justify sending to OEIS.
Nevertheless, 20 years later when I mentioned these "arbitrary" inventions to seqfan [19], it turned out people actually liked the idea. So, this and a few others (see my Accelerating Sequences page for more) were immediately added to OEIS.
Denominators of continued fraction convergents to √699 (A42345)
1, 2, 7, 9, 16, 41, 57, 1466, 1523, 4512, 6035, 10547, 37676, 85899, A042345 4504424, 9094747, 31788665, 40883412, 72672077, ...
This is an example from a set of nearly 2000 sequences that were all added at once, automatically generated by a computer program. One day in the 1990's, the OEIS was diluted by 5% in an instant.
A0 = 0; A1 = -1; AK+1 = AK + K AK-1 + K (my "MCS3444773")
0, -1, 0, 0, 3, 7, 27, 75, 271, 879, 3327, 12127, 48735, 194271, 827839, 3547647, 15965247, 72727615, 344136831, 1653233919, 8191833727, 41256512127, ...
In one hour, my sequence-searching program MCS generates this and billions of similar sequences given by a direct formula or recurrence relation.
Mu-molecules in Mandelbrot set whose seeds have period n. (A6876)
1, 0, 1, 3, 11, 20, 57, 108, 240, 472, 1013, 1959, 4083, 8052, 16315, 32496, 65519, 130464, 262125, 523209, 1048353, 2095084, 4194281, 8384100, 16777120, ...
See R. P. Munafo, enumeration of features (part of Mu-Ency - The Encyclopedia of the Mandelbrot Set).
I submitted this to N.J.A. Sloane in the early 1990's and it was printed in the 1995 book [15]. It had not been published anywhere before, thus violating my own belief in the 1973 "rule 4".
Sum of digits of the LCM of the Nth primitive Pythagorean triple (my "X900013")
6, 15, 6, 6, 12, 15, 18, 27, 12, 18, 6, ...
The primitive Pythagorean triples are from A103606; thus the LCM of (3,4,5) is 60, and sum of digits is 6; the LCM of (5,12,13) is 780 and sum of digits is 15, etc.
This is an example of Alonso del Arte's concept of "contrived" definitions like f(g(h(N))). Here f() is "sum of digits"; g() is "least common multiple", and h() is Pythagorean triple.
Ironically, when I noticed that they're all multiples of 3, a little voice in my head said hey maybe this seq is interesting...!. He who listens to that voice is a blind man following a fool.
Of course, these are primitive Pythagorean triples, meaning they have no common factor, and thus it is guaranteed that exactly one of A, B and C must be divisible by 3. So their LCM (which happens to also be their product A×B×C) will always be a multiple of three. And thus, the additive digital root (A10888, a fancy way of saying "casting out nines") will also be a multiple of 3. Q.E.D.
Despite all this intellectual-sounding detail, X900013 is not worthy of the OEIS because all of this stuff isn't actually saying anything!
Strobogrammatic numbers: the same upside down (A0787) (also called ambigrams).
0, 1, 8, 11, 69, 88, 96, 101, 111, 181, 609, 619, 689, 808, 818, 888, 906, 916, 986, 1001, 1111, 1691, 1881, 1961, 6009, 6119, 6699, 6889, 6969, 8008, 8118, 8698, 8888, 8968, ...
This was sequence N1897 in Sloane's 1973 book, and M4480 in the Sloane/Plouffe 1995 book. Since it depends both on base 10 and the visual appearance of the ten digits, it reeks of cultural specificity.
I also think of this as lacking "objective truth" because you'd need to be using the same type of number system, with the same visual properties of the ten digits, in order to discover the sequence. But to be pedantic about it, the sequence is well-defined, so I suppose the aliens on Vega would discover it eventually if they bothered to try all combinations of bases and digits.
Numbers which when displayed on a calculator and viewed upside-down resemble words from the National Scrabble Association Dictionary (my "X900012")
10, 14, 15, 17, 18, 30, 34, 38, 40, 43, 45, 50, 51, 53, 73, 135, 137, 149, 180, 304, 314, 317, 319, 335, 337, 338, 339, 345, 350, 370, 380, 400, 434, 445, 504, 505, 508, 509, 514, 515, 517, 518, ...
3 is "E" upside down; 4 is "h" upside-down, and so on. Thus the number 338 becomes "BEE",400 becomes "OOh", etc.
The two-letter words (with brief definitions) are in: Mike Wolfberg, All 101 Two-Letter Words
This example breaks all of the "cultural-specific" rules at once: it is tied to base 10, the English language, and the shape of the ten digits in European-Arabic notation as adapted for a calculator, not to mention many arbitrary choices of which letter combinations are "words". Proper nouns, acronyms, and alternate spellings are excluded, except the ones that aren't.
Local stops on New York City Broadway line subway (A0053)
14, 18, 23, 28, 34, 42, 50, 59, 66, 72, 79, 86, 96, 103, 110, 116, 125, 137, 145, 157, 168, 181, 191, 207, 215, 225, 231, 238, 242
Not only is this one terribly culturally specific, but it changes with time (thus is neither well-defined nor objectively true) and is finite (violating rule 2 of 4)!
An example of junk (my "X900011")
193, 344, 111, 992, 232, 159, 160, 756, 349
27 random digits I made up in a drowsy stupor, then capriciously severed into groups of three.
Author: Robert Munafo, 2013 Jan 24
1 : When editing or submitting a sequence to the OEIS, users are advised:
IMPORTANT: Thousands of people use the sequence database every day.
Please take great care that the terms you send are absolutely correct.
The standards are those of a mathematics reference work.
Contributions are contributed under
The OEIS Contributor's License Agreement,
and may be edited, altered, or removed by other
contributors. If you do not want your writing to be edited
mercilessly, then do not submit it here.
You are also promising us that you wrote this yourself, or copied
it from a public domain resource, or have the right to submit it (see
The OEIS Contributor's License Agreement for details). Do not submit
copyrighted work without permission!
Much of this is fairly standard boilerplate seen on other Wikis, as you'll find by a web search for the phrase "writing to be edited mercilessly".
2 : Mankoff [22] says much about why things are funny. In this case, it's because the caption evokes two interpretations: that of the original un-modified statement, and that of the altered version referencing Hubble's law. For the caveats, see the next note.
3 : The Hubble's car cartoon wouldn't be funny if you picked just any word to change, and most choices of the new word wouldn't work either. This one works because "closer" and "bluer" are both qualities that can reasonably be applied generally to "objects", and because if the car is moving forward (a reasonable assumption) then the objects in the mirror would actually be redshifted a tiny bit, making the altered phrase actually true.
There is also a more subtle, deeper nerd humor in the wording: since light travels at a finite speed, at any instant the objects seen in a mirror are a bit further than they were when the light that is being seen left the object. Thus, if the mirror were flat, the "closer than they appear" statement would actually be false. To this pedantic nerd instinct, the thus-corrected phrase "further than they appear" would be expected or familiar, like an oft-repeated punchline, making "bluer than they appear" unexpected and therefore funny.
Pedantic correction (a familiar example questions the phrase "head over heels in love": shouldn't it be "heels over head"?) is a nerdy form of single-point mutation humor which xkcd uses quite a lot. In this particular case though, the mirror as drawn is clearly curved (convex).
4 : In full, here are the criteria used by N.J.A. Sloane for deciding whether to include a sequence in his 1973 book [13] :
1.5 WHAT SEQUENCES ARE INCLUDED?
Rule 1 The sequence must consist of nonnegative integers. (Sequences alternating in sign have been replaced by their absolute values. Interesting sequences of fractions have been entered by numerators and denominators separately. Some sequences of real numbers have been replaced by their integer parts, others by the nearest integers.)
Rule 2 The sequence must be infinite.
A few, like the Mersenne primes, have been given the benefit of the doubt.
Rule 3 The first two terms must be 1, n, where n is between 2 and 999.
An initial 1 has been silently inserted before the first term if this is greater than 1, and extra 1's and 0's at the beginning have been silently deleted.
Rule 4 The sequence should have appeared in the scientific literature, and must be well-defined and interesting.
The selection has inevitably been subjective, but the goal has been to include a broad variety of sequences and as many as possible.
5 : Another editor helped me see how poor my criteria (such as my desire for things to be published first, independent of base 10 or a specific culture or language, applicable to more than one unrelated problem in math or science, etc.) would be for judging what has actually been accepted to the OEIS recently. In dismay, I wrote:
This is the problem we face with the "netiquette for newbies" issue. I imagine that I am not alone amongst the editors in saying this. I struggle with my evident prejudice, and grasp at simple, automatic or objective tests that would fail to actually promote quality and fairness.
6 : See Message from Vega (part of the 1997 movie Contact). It is perhaps my favorite statement on the clash between pop culture, junk science, religion, and human inquisitiveness.
7 : I am reminded of Hofstadter's diagram referring to the effort of mathematicians to demarcate truth from falsehood :

Douglas Hofstadter's illustration from [14]
depicting the collective effort of mathematicians (such as Russell
and Whitehead [11]) to uncover the whole of
Objective Truth via mathematical theorem-proving. Note the relatively
large size of the unexplored area between the well-defined trees of
Theorems and Negations of Theorems.
but in our case it's even worse.
[8] The diagrams (of a circle with diameter, radius and area; and a triangle with Pythagorean theorem) are based on the "Page on Geometry" of the Dutil-Dumas Cosmic Call (more links at Yvan Dutil). The writing uses a simple substitution cypher, and the bits of "alien" text (actually Yi script) represent "R", "=2×R", "=2×R×π", "=π×R^2", "A", "B", "C", and "A^2+B^2=C^2". Image by Robert Munafo.
[9] Car rear-view mirror bearing the inscription "OBJECTS IN MIRROR ARE BLUER THAN THEY APPEAR" and the caption "EDWIN HUBBLE'S CAR". xkcd 1125 by Randall Munroe.
[10] The numbers 30, 34, etc. in a calculator font, and the same numbers upside down. Image by Robert Munafo, using the font "SF Digital Readout" from ShyFoundry.com
Listed in chronological order, because that's the only correct way :-P
[11] A.N. Whitehead and Bertrand Russell, Principia_Mathematica (three volumes), 1910-1913. Intended to establish a structure within which the whole of mathematical truths could be proven, PM instead became the straw man for Gödel's first (and more famous) incompleteness theorem. Even in highly formalized domains, it is impossible to rigidly define the whole of objective truth. (This situation is a primary subject of [14]).
[12] G.H. Hardy and E.M. Wright, An introduction to the theory of numbers. University of Oxford (1938). ISBN 0-199-21986-9.
The full paragraph from the introduction is:
We have often allowed our personal interests to decide our programme, and have selected subjects less because of their importance (though most of them are important enough) than because we found them congenial and because other writers have left us something to say. Our first aim has been to write an interesting book, and one unlike other books. We may have succeeded at the price of too much eccentricity, or we may have failed; but we can hardly have failed completely, the subject-matter being so attractive that only extravagant incompetence could make it dull.
[13] Neil J. A. Sloane, A Handbook of Integer Sequences, Academic Press (1973), ISBN 0-12-648550-X.
[14] Hofstadter, Douglas, Goedel, Escher Bach: An Eternal Golden Braid, Vintage, 1979, ISBN 978-0394745022
[15] Neil J.A. Sloane and Simon Plouffe, The Encyclopedia of Integer Sequences, Academic Press (1995), ISBN 0-12-558630-2.
This book contains some of my own submissions (such as the Mandelbrot sequences A006874 through A006876), nearly all of which violated my own standards of submission, insomuch as they had not been previously published.
[16] N.J.A. Sloane, the OEIS Foundation, and contributors, On-Line Encyclopedia of Integer Sequences, online database with custom search engine, and an associated collaborative content editing and management system including a Wiki.
[17] Robert Munafo, Minimally Complex Sequences.
This was a project I began in 2004 to enumerate recurrence relations of low Kolmogorov complexity. The online version now includes over 3000 sequences. Many are clearly of interest, but others (for example MCS981) hardly seem to deserve an entry.
[18] Robert Munafo, Recent Additions to Sloane's Database of Integer Sequences. I put stuff here before I submit it, or sometimes with no intention of ever submitting.
[19] Discussions on the seqfan mailing list, late 2009 and early 2010.
[20] Alonso del Arte, Is this sequence interesting, wiki article, 2012.
[21] Charles Greathouse, Is this sequence interesting, wiki article, 2012.
[22] Robert Mankoff, First Things First (Unless They're Second) column article for New Yorker magazine, 2012 Aug 22.
Analysis of cartoons and humor in general is one of the more common themes in Mankoff's writing. There is also at least one relevant book, The Naked Cartoonist.
[23] Antti Karttunen cited some of his "boring auxiliary and utility-sequences" in discussion on [24].
[24] Discussions on OEIS editors' mailing list, 2013.
This page was written in the "embarrassingly readable" markup language RHTF, and was last updated on 2018 Feb 04.
 s.27
s.27