Sequence A169720, and two others by Alice V. Kleeva
This page illustrates a few mysterious and confusing OEIS sequences submitted in 2010 by Alice V. Kleeva.
Contents
A169720
This sequence, Sloane's A169720, includes some of the triangular numbers identified with a certain geometrical grid construction by Alice Kleeva of the Hermitage Museum in St. Petersburg. You may read her description (as paraphrased by Neil Sloane) here on seqfan.
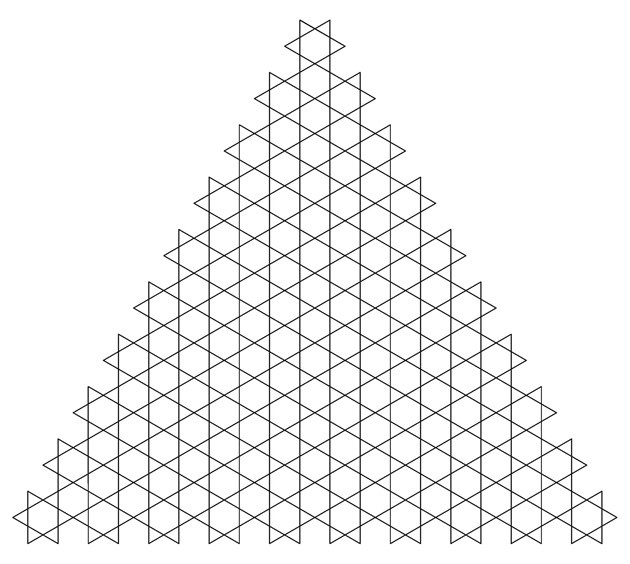
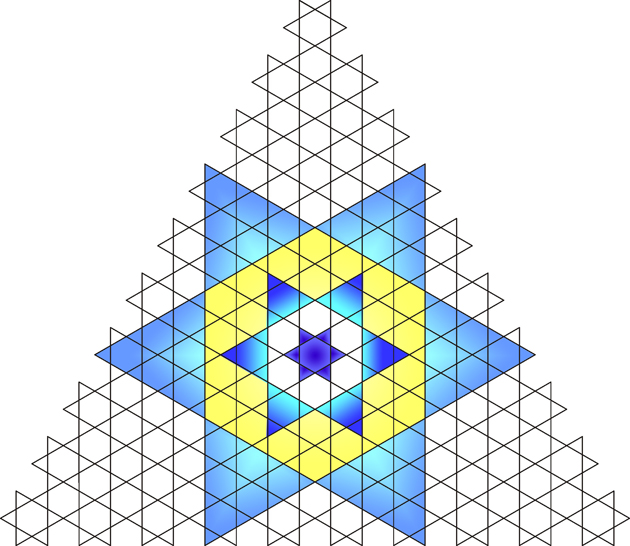
The sequence A169720 begins: 1, 10, 55, 253, 1081, ... By means of illustration, the author provided the following figures:
|
The figures provide too much, and at the same time too little, explanation. The sequence is actually constructed as follows:
1. Start with the central points of a hexagonal grid, or the vertices of a triangular grid:
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .2. Draw concentric 6-pointed star (also known as "Star of David") figures in the grid. Make each star just large enough so that its central hexagon surrounds, but does not intersect, the 6-pointed star within its center:
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . x . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . x x . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . x . x . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . x . . x . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . x . . . x . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . x . . . . x . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . x . . . . . x . . . . . . . . . . . . . . . . . . . . . . x x x x x x x x x x x x x x x x x x x x x x . . . . . . . . . . . . . . . . x . . . . . x . . . * . . . x . . . . . x . . . . . . . . . . . . . . . . x . . . . x . . . * * . . . x . . . . x . . . . . . . . . . . . . . . . . . x . . . x . . . * . * . . . x . . . x . . . . . . . . . . . . . . . . . . x . . x * * * * * * * * * * x . . x . . . . . . . . . . . . . . . . . . . . x . x . * . * . o . * . * . x . x . . . . . . . . . . . . . . . . . . . . x x . . * * o o o o * * . . x x . . . . . . . . . . . . . . . . . . . . . . x . . . * . o 0 o . * . . . x . . . . . . . . . . . . . . . . . . . . . x x . . * * o o o o * * . . x x . . . . . . . . . . . . . . . . . . . . . x . x . * . * . o . * . * . x . x . . . . . . . . . . . . . . . . . . . x . . x * * * * * * * * * * x . . x . . . . . . . . . . . . . . . . . . . x . . . x . . . * . * . . . x . . . x . . . . . . . . . . . . . . . . . x . . . . x . . . * * . . . x . . . . x . . . . . . . . . . . . . . . . . x . . . . . x . . . * . . . x . . . . . x . . . . . . . . . . . . . . . x x x x x x x x x x x x x x x x x x x x x x . . . . . . . . . . . . . . . . . . . . . . . x . . . . . x . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . x . . . . x . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . x . . . x . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . x . . x . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . x . x . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . x x . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . x . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .(The first 6-pointed star is represented by a single point in the center; the next one consists of the vertices labeled "o"; the next consists of "*", the next consists of "x", and there would be more larger ones around that.)
3. Replace each star with a filled triangle and count the number of points in the triangle:
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 0 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A[1] = 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . o . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . o o . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . o o o . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . o o o o . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A[2] = 10 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . * * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . * * * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . * * * * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . * * * * * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . * * * * * * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . * * * * * * * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . * * * * * * * * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . * * * * * * * * * . . . . . . . . . . . . . . . . . . . . . . . . . . . * * * * * * * * * * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A[3] = 55 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . x . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . x x . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . x x x . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . x x x x . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . x x x x x . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . x x x x x x . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . x x x x x x x . . . . . . . . . . . . . . . . . . . . . . . . . . . . . x x x x x x x x . . . . . . . . . . . . . . . . . . . . . . . . . . . . . x x x x x x x x x . . . . . . . . . . . . . . . . . . . . . . . . . . . x x x x x x x x x x . . . . . . . . . . . . . . . . . . . . . . . . . . . x x x x x x x x x x x . . . . . . . . . . . . . . . . . . . . . . . . . x x x x x x x x x x x x . . . . . . . . . . . . . . . . . . . . . . . . . x x x x x x x x x x x x x . . . . . . . . . . . . . . . . . . . . . . . x x x x x x x x x x x x x x . . . . . . . . . . . . . . . . . . . . . . . x x x x x x x x x x x x x x x . . . . . . . . . . . . . . . . . . . . . x x x x x x x x x x x x x x x x . . . . . . . . . . . . . . . . . . . . . x x x x x x x x x x x x x x x x x . . . . . . . . . . . . . . . . . . . x x x x x x x x x x x x x x x x x x . . . . . . . . . . . . . . . . . . . x x x x x x x x x x x x x x x x x x x . . . . . . . . . . . . . . . . . x x x x x x x x x x x x x x x x x x x x . . . . . . . . . . . . . . . . . x x x x x x x x x x x x x x x x x x x x x . . . . . . . . . . . . . . . x x x x x x x x x x x x x x x x x x x x x x . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A[4] = 253A169727
Sequence A169727 is illustrated by two similarly uninformative figures:
|
The sequence starts: 1, 19, 127, 631, 2791, ... and is a subsequence of A003215.
Contrary to the seeming complexity of the figures, the sequence is constructed almost the same way as A169720, with a series of concentric 6-pointed stars on a grid. Only the third step is different:
Step 3 for A169727. Count the number of points inside each star's central hexagon:
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . o . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . o o o o . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . o 0 o . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . o o o o . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . o . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (1st star, interior has just one '0') A[1] = 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . * * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . * . * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . * * * * * * * * * * . . . . . . . . . . . . . . . . . . . . . . . . . . . . * . * o o o * . * . . . . . . . . . . . . . . . . . . . . . . . . . . . . * * o o o o * * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . * o o o o o * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . * * o o o o * * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . * . * o o o * . * . . . . . . . . . . . . . . . . . . . . . . . . . . . * * * * * * * * * * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . * . * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . * * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (2rd star, interior filled with 'o') There are 19 o's. A[2] = 19 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . x . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . x x . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . x . x . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . x . . x . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . x . . . x . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . x . . . . x . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . x . . . . . x . . . . . . . . . . . . . . . . . . . . . . x x x x x x x x x x x x x x x x x x x x x x . . . . . . . . . . . . . . . . x . . . . . x * * * * * * * x . . . . . x . . . . . . . . . . . . . . . . x . . . . x * * * * * * * * x . . . . x . . . . . . . . . . . . . . . . . . x . . . x * * * * * * * * * x . . . x . . . . . . . . . . . . . . . . . . x . . x * * * * * * * * * * x . . x . . . . . . . . . . . . . . . . . . . . x . x * * * * * * * * * * * x . x . . . . . . . . . . . . . . . . . . . . x x * * * * * * * * * * * * x x . . . . . . . . . . . . . . . . . . . . . . x * * * * * * * * * * * * * x . . . . . . . . . . . . . . . . . . . . . x x * * * * * * * * * * * * x x . . . . . . . . . . . . . . . . . . . . . x . x * * * * * * * * * * * x . x . . . . . . . . . . . . . . . . . . . x . . x * * * * * * * * * * x . . x . . . . . . . . . . . . . . . . . . . x . . . x * * * * * * * * * x . . . x . . . . . . . . . . . . . . . . . x . . . . x * * * * * * * * x . . . . x . . . . . . . . . . . . . . . . . x . . . . . x * * * * * * * x . . . . . x . . . . . . . . . . . . . . . x x x x x x x x x x x x x x x x x x x x x x . . . . . . . . . . . . . . . . . . . . . . . x . . . . . x . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . x . . . . x . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . x . . . x . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . x . . x . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . x . x . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . x x . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . x . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (3rd star, interior filled with '*') There are 127 *'s. A[3] = 127A169726
Sequence A169726, once again, has two confusing figures:
|
The sequence starts: 1, 7, 37, 169, 721, 2977, ... and like A169727 it is a subset of A003215.
I won't bother to illustrate the construction, but it is very similar to that for A169727, again we are counting the points inside the central hexagon of each in a series of concentric 6-pointed stars. These central hexagons are white in the second figure above.
As it turns out, the terms in this sequence are just the next term (from A003215) after those A003215 terms that appear in A169727. In other words:
1. Start with A169727, which is: 1, 19, 127, 631, 2791, ...
2. Replace each term with the next term from A003215. 1 becomes 7; 19 becomes 37; 127 becomes 169; 631 becomes 721; and so on. We get: 7, 37, 169, 721, 2977, ...
3. Add an initial 1. Now we have A169726: 1, 7, 37, 169, 721, 2977, ...
Footnotes
This page was written in the "embarrassingly readable" markup language RHTF, and was last updated on 2025 Apr 26.
 s.27
s.27