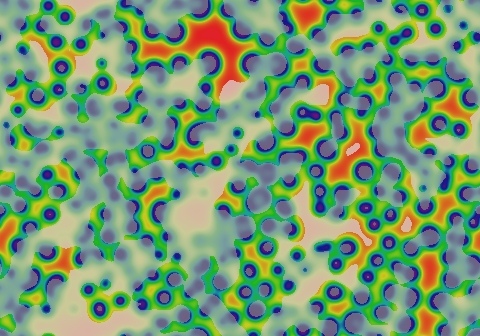
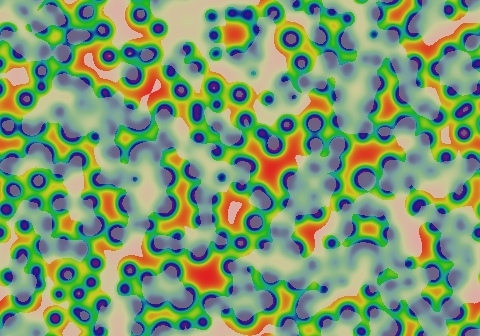
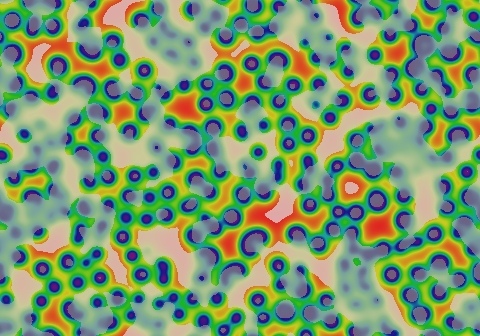
Gray-Scott Model at F 0.0180, k 0.0530
These images and movie demonstrate the behavior of the Gray-Scott reaction-diffusion system with σ=Du/Dv=2 and parameters F=0.0180, k=0.0530.
Spots and rings grow, initially with smooth outer edges, then bending into clovers. When two fronts collide they annihilate and fade; the fading pattern then usually spawns a new growing spots. These new spots are of two types, simple spots (generally small) and "C" shapes that move while growing and generate more spots in their wake. (glossary of terms)
 increase F increase F
 | |||
 decrease k  |


|
15 frames/sec.; each fr. is 30 iter. steps = 15 tu; 1800 fr. total (27,000 tu) | 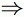 increase k 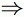
|
|
| ||
 decrease F decrease F
 |
In these images:
- Color indicates level of u, ranging from purple (lowest u values) through blue, aqua, green, yellow and pink/red (highest u values)
- Areas where u is increasing are lightened to a light pastel tone; where u is decreasing the color is vivid.
- In areas where u is changing by less than ±3×10-6 per tu, an intermediate pastel color is seen. This includes areas that are in steady state or equilibrium.
''tu'' is the dimensionless unit of time, and ''lu'' the dimensionless unit of length, implicit in the equations that define the reaction-diffusion model. The grids for these simulations use Δx=1/143 lu and Δt=1/2 tu; the system is 3.2 lu wide. The simulation meets itself at the edges (periodic boundary condition); all images tile seamlessly if used as wallpaper.
Go back to Gray-Scott pattern index
This page was written in the "embarrassingly readable" markup language RHTF, and was last updated on 2015 Nov 07.
 s.27
s.27