Large Numbers
First page . . . Back to page 10
Footnotes
1 : http://www.sizes.com/numbers/big_numName.htm Anonymous author at "sizes.com", Names of big numbers, 2004.
2 : http://www.miakinen.net/vrac/nombres#lettres_zillions Olivier Miakinen, Écriture des nombres en français, (web page) 2003.
3 : http://web.archive.org/web/20061021030550/http://www.io.com/~iareth/bignum.html Gregg William Geist, Big Numbers (web page), 2006 (Latin number names, some of the large examples like centumsedecillion)
4 : http://www.miakinen.net/vrac/zillions Olivier Miakinen, Les zillions selon Conway, Wechsler... et Miakinen (web page), 2003.
5 : http://www.graner.net/nicolas/nombres/wechsler.txt Allan Wechsler, "Re: Number names" (newsgroup message), 2000.
6 : The Oxford English Dictionary (Second Edition), 1989, entry for million (vol. IX, pp. 784-785), sense 1. a. (a)
7 : Conway and Guy, The Book of Numbers. See bibliography entry [48] below.
8 : http://yudkowsky.net/singularity.html Eliezer Yudkowsky, Staring into the Singularity, web page (1996-2001).
9 : Olivier Miakinen, personal communication, Sep 2004.
10 : http://www.polytope.net/hedrondude/illion.htm Jonathan Bowers (AKA "hedrondude"), -Illion Numbers. Extensive list of his invented large number names, in numerical order, and most ending in "-illion".
11 : Stephen Hawking, God Created the Integers (an anthology of translated works of great mathematicians throughout history), pp. 971-1039 (Georg Cantor)
12 : http://www.toothycat.net/wiki/wiki.pl?CategoryMaths/BigNumbers Douglas Reay, commenting on discussion of formal theory of computation, toothycat.net wiki (created by Sergei and Morag Lewis), CategoryMaths, BigNumbers.
13 : https://u.osu.edu/friedman.8/foundational-adventures/downloadable-manuscripts/ (formerly at www.math.ohio-state.edu/~friedman/manuscripts.html) Papers by Harvey M. Friedman. In the "lecture notes" section is Enormous Integers in Real Life, 2000, which summarises several methods of producing large integers, related to combinatorics and theory of computation.
14 : Harvey Friedman, Long Finite Sequences, 1998. Available at the above website13.
15 : http://math.eretrandre.org/tetrationforum/showthread.php?tid=184 Henryk Trappman and Andrew Robbins, Tetration FAQ (online document)
Note: A previous version was here
16 : Martin Gardner, The Colossal Book of Mathematics: Classic Puzzles, Paradoxes, and Problems, W. W. Norton (2001), ISBN 0393020231.
The "Graham-Gardner number": pp. 448-450; also appeared in Scientific American in November 1977.
Most Gardner material has been published multiple times, so you might find it in one or another of his earlier books.
17 : Knuth, Donald E., Coping With Finiteness, Science vol. 194 n. 4271 (Dec 1976), pp. 1235-1242.
18 : http://www.stars21.com/translator/english_to_latin.html InterTran English-Latin Translator, via Stars21.
19 : Wikipedia, Names of large numbers, encyclopedia article (accessed January 2010)
20 : http://www.numericana.com/answer/units.htm#prefix G{'e}rard P. Michon's Numericana, Final Answers — Measurements and Units. (Has lots of details about real and bogus SI prefixes) (formerly at http://home.att.net/~numericana/answer/units.htm)
21 : billion in the literal sense appears first in 1690, when it unambiguously meant 1012. The same applies to the first literal usage of trillion (1018) and all of the higher names in the table — so these citation dates merely indicate how old the words are. See my discussion History of Short vs. Long Scale for more details. All first citations in OED [47] are either from Jeake in 1674 or Locke in 1690.
22 : OED [47] does not cite billion in the superlative sense, but milliard was used in the superlative sense as far back as 1823.
23 : OED [47] cites one usage of sextillion in the superlative sense by Walt Whitman in 1881; earlier editions of Whitman's poetry collection show that he used this word and several others as early as 1855, and trillions in 1847. Whitman also used decillion as a superlative, and he used millions in the superlative sense more than all the other -illions combined. H. P. Lovecraft used vigintillion in the superlative sense in 1926 and 1928, and used no other -illion words above billion; his usage of million and billion was literal in almost all cases.
24 : duodeviginti, undeviginti : These are two of the more notable discrepancies with actual Latin number-names; see the discussion here.
25 : Typically the terms of such a competition require that each number be finite, "well-defined", and "computable"; this last requirement keeps the discussion within the realm of things that can be proven. (Without it, the busy beaver functions prevail, but it becomes nearly impossible to resolve the question of whose function is larger).
An example of such a discussion is the long-running xkcd forum discussion thread "My number is bigger!". This thread was begun on the 7th of July, 2007, and remained continually active for nearly three years (last checked May 2010). The initial message began the competition with 9000; the first respondent offered 3.250792...×10548; several class 2 replies brought it up to 3.454307...×101661; then it jumped to 101010, 10101010, 10↑↑512, and 10↑↑↑3=10↑↑(10↑↑10). All of this was within the first 24 hours. Up-arrow notation was no longer of any use by the third day of the discussion, and the participants then began defining recursive functions and discussing proofs. It continued along those lines for the following three years.
26 : See "Completeness of the S-K basis" on the Wikipedia page for Combinatory logic,
40 : "Sbiis Saiban" is a large numbers enthusiast using a pseudonym.
41 : Adam Goucher, graph minors
42 : Adam Goucher, comment in discussion of the TREE[] function.
Bibliography
[30] W. Stanley Jevons, The Power of Numerical Discrimination, Nature vol. 3, pp. 281–282 (9 February 1871) "It is well known that the mind is unable through the eye to estimate any large number of objects without counting them successively. A small number, for instance three or four, it can certainly comprehend and count by an instantaneous and apparently single act of mental attention." (emphasis added) Performs an experiment to quantify the estimation error as a function of how many (identical) objects are viewed; and quotes earlier writers on the same topic.
[31] Edward Brooks, The Philosophy of Arithmetic, 1904. Cited by [38].
[32] Edward Kasner and James Newman, Mathematics and the Imagination, Penguin, 1940
[33] Reuben Goodstein "On the restricted ordinal theorem", Journal of Symbolic Logic, 9 (2): 33–41, 1944.
[34] George Gamow, One, Two, Three... Infinity: Facts and Speculations of Science, Viking, 1947 (reprinted in paperback by Dover, 1988).
This was an early source for me and unfortunately gave me the impression that the contimuum hypothesis had been proven. This figure implies that the ℵn series of infinities is the complete set of infinities:
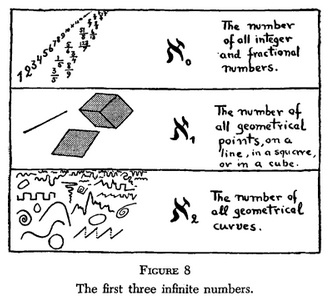
Gamow p. 23., implying CH
If these are really "the first three infinite numbers", then there can be nothing between ℵ0 and ℵ1, and that's CH.
[35] E. L. Kaufman, et. al., 1949: The discrimination of visual number. The American Journal of Psychology 62(4) (Oct. 1949), pp. 498-525. To subitize is defined as "To judge (the number of objects in a group) rapidly, accurately and confidently without counting them"
[36] George Miller, The magical number seven plus or minus two: some limits on our capacity for processing information. The Psychological Review 63 (1956), pp. 81-97 In a variety of psychological experiments (of the basic kind that measure nothing more complicated than the ability to accurately distinguish different magnitudes of physical sensory inputs) they show that humans can typically distinguish at most n different levels of any particular magnitude, with n varying by the type of sensation and with n values clustered around 7.
[37] Philip J. Davis, The Lore of Large Numbers, New York: Random House, 1961
Much discussion of number writing systems, methods of arithmetic and estimation, names for large powers of 10, and so on. Covers many other topics, including: the method of finite differences; linear algebra and finite-element analysis; figurate sequences, prime numbers; large and small quantities encountered in science; SI prefixes and unit conversion.
This is one of the first books I found on the topic. Bits of it (such as the discussion of how many objects one can see at one time with one's eyes) are seen on this web page.
[38] Dmitri Borgmann, Naming the numbers. Word Ways: the Journal of Recreational Linguistics 1 (1), pp. 28-31, 1968. Cover and contents are here and article is here.
[39] Howard DeLong, A profile of mathematical logic (Addison-Wesley 1970, also Dover 2004) p. 192.
[40] R.L. Graham and B.L. Rothschild, Ramsey's Theorem for n-Parameter Sets. Transactions of the American Mathematical Society 159 (1971), 257-292. (Another PDF is here).
[41] Douglas Hofstadter, Gödel, Escher Bach: An Eternal Golden Braid, Vintage, 1979, ISBN 978-0394745022
[42] Philip Davis, and Reuben Hersh, The Mathematical Experience, Birkhaeuser, 1981.
infinities: pages 223-225
[43] Donald E. Knuth, Supernatural numbers. Appears as pp. 310-325 in The Mathematical Gardner, ed. David A. Klarner (1981).
[44] Douglas R. Hofstadter, On Number Numbness, Mathematical Recreations column, Scientific American, May 1982.
[45] Dewdney, A.K., The Busy Beaver, in Mathematical Recreations column, Scientific American, April 1985, p. 30.
[46] Douglas R. Hofstadter, Metamagical Themas, book collecting several articles from the Scientific American column of the same name, BasicBooks (1985), ISBN 0-465-04540-5.
[47] The Compact Oxford English Dictionary (Second Edition), 1991. This is the version that has 21473 pages photographically reduced into a single book of about 2400 pages.
[48] John Horton Conway and Richard Guy, The Book of Numbers, Springer-Verlag, New York, 1996. ISBN 038797993X.
Page numbers for specific topics:
pp. 13-15 (-illion number-names)
pp. 59-61 (Knuth up-arrow notation)
p. 60 (Ackermann numbers)
p. 61 (Conway chained-arrow notation)
p. 61 (Skewes's number)
pp. 61-62 (the "Graham-Conway number")
pp. 266-276 (Cantor ordinal infinities)
pp. 277-282 (cardinal infinities and the continuum)
[49] Crandall, The Challenge of Large Numbers, Scientific American February 1997, pages 74-79.
[50] Georges Ifrah, The Universal History of Numbers, ISBN 0-471-37568-3. (1999).
[51] Alistair Cockburn, A 'fuga' really big numbers, blog article, 2000 Jan 3rd; republished by the American Physical Society here on the 1st April 2001.
[52] Alistair Cockburn and others, "Really Big Numbers", discussion on c2.com, 2nd June 2002.
[53] Chris Bird, Proof that Bird's Linear Array Notation with 5 or more entries goes beyond Conway's Chained Arrow Notation, 2006. Available here (and formerly at uglypc.ggh.org.uk/chrisb/maths/superhugenumbers/array_notations.pdf)
[54] Harvey Friedman, n(3) < Graham's number < n(4) < TREE{3}, message to FOM (Foundations of Mathematics) mailing list.
[55] A. Nabutovsky and S. Weinberger, Betti numbers of finitely presented groups and very rapidly growing functions, 2007. Available here
[56] Chris Bird, personal communication, 2008.
[57] Donald E. Knuth, personal communication, 2010 Feb 26.
[58] N. Mohan Kumar, Construction of Number Systems (for Math 310 course at Washington University in St. Louis), 2011.
[59] John Baez, Google+ post, 2013 Jan 11 (See also this mathoverflow question)
[60] Sbiis Saibian40, 3.2.10 Graham's Number, web article, 2022 January 24.
[61] Sbiis Saibian40, A Theorem for Knuth-Arrows, 2014 May 21.
[62] Adam Goucher, The Ξ function (blog article), 2013 Jan 6.
[63] Michael Taylor, Numbers, 2014.
Other Links
Aaronson, Scott, Who Can Name the Bigger Number?, essay about how to win the often-contemplated contest; covers many of the topics discussed here.
Bird, Chris, Array Notations for Super Huge Numbers, 2006. (An older version of his work, which includes much of the material found here).
----, Super Huge Numbers, 2012. There are several sections, with the simplest and slowest-growing functions first. The initial chapter "Linear Array Notation" is roughly comparable to Bowers arrays; the other chapters define higher and higher recursive functions.
Bowers, Jonathan, Big Number Central.
----, Exploding Array Function.
----, Infinity Scrapers.
Hudelson, Matt, Extremely Large Numbers
Knuth, Mathematics and Computer Science: Coping with Finiteness. Advances in our ability to compute are bringing us substantially closer to ultimate limitations., Science, 1976, pages 1235-1242
Kosara, Robert, The Ackermann Function
MacTutor history of Mathematics page on Chuquet
Matuszek, David, Ackermann's Function
McGough, Nancy, The Continuum Hypothesis (web pages)
Munafo, Robert, hypercalc (the Perl calculator program that handles numbers up to 10④10000000000)
Pilhofer, Frank, Googolplex and How to get a Googolplex
Rado, Tibor, On non-computable functions, Bell System Tech. Journal vol. 41 (1962), pages 877-884. (busy beaver function)
Rucker, Rudy, Infinity and the Mind, 1980. (ordinal infinities: the relevant chapter was reproduced here the last time I checked.)
Spencer, Large Numbers and Unprovable Theorems, American Mathematical Monthly, 1983, pages 669-675
Steinhaus, Hugo, Mathematical Snapshots (3rd revised edition) 1983, pp. 28-29.
Stepney, Susan, Ackermann's function
----, Big Numbers
----, Graham's Number (referring to the more well-known version, i.e. the "Graham-Gardner number")
Teoh, H. S., The Exploding Tree Function, 2008.
Weisstein, Eric (ed.), Ackermann Function
----, Large Number
Wikipedia, Veblen function.
Acknowledgments
To Morgan Owens (packrat at mznet gen nz) for news of the Knuth -yllion names and the Busy Beaver function
Unconfirmed SI prefixes: Sci.Math FAQ, Alex Lopez-Ortiz, ed. (formerly at http://www.cs.unb.ca/~alopez-o/math-faq/mathtext/node25.html)
Japanese readers should see: 巨大数論 (from @kyodaisuu on Twitter)
If you like this you might also enjoy my numbers page.
s.30